Why Beauty is Truth (17 page)
Read Why Beauty is Truth Online
Authors: Ian Stewart


Around this time, mathematicians were gradually coming to realize that although “complex” numbers seemed artificial and their meaning incomprehensible, they made algebra much neater by providing solutions to equations in a uniform way. Elegance and simplicity are the touchstones of mathematics, and novel concepts, however strange they appear at first, tend to win out in the long run if they help to
keep
the subject elegant and simple.
If you work purely with traditional “real” numbers, equations can be annoyingly erratic. The equation
x
2
â 2 = 0 has two solutions, plus or minus the square root of two, but the very similar equation
x
2
+ 1 = 0 has none at all. However, this equation has two solutions in complex numbers:
i
and â
i
. The symbol
i
for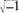 was introduced by Euler in 1777 but not published until 1794. A theory couched solely in terms of “real” equations is littered with exceptions and pedantic distinctions. The analogous theory of complex equations avoids all of these complications by swallowing wholesale one big complication at the very outset: to allow complex numbers as well as real ones.
was introduced by Euler in 1777 but not published until 1794. A theory couched solely in terms of “real” equations is littered with exceptions and pedantic distinctions. The analogous theory of complex equations avoids all of these complications by swallowing wholesale one big complication at the very outset: to allow complex numbers as well as real ones.
By 1750, the circle of ideas initiated by the mathematicians of Renaissance Italy had matured and closed. Their methods for solving cubic and quartic equations were seen as natural extensions of the Babylonian solution of quadratics. The connection between radicals and complex numbers had been worked out in some detail, and it was known that in this extension of the usual number system, a number had not one cube root but three; not one fourth root but four; not one fifth root but five. The key to understanding where these new roots came from was a beautiful property of “roots of unity,” that is,
n
th roots of the number 1. These roots form the vertices of a regular
n
-sided polygon in the complex plane, with one vertex at 1. The remaining roots of unity space themselves out equally around a circle of radius 1, centered at 0. For instance, the left-hand figure (next page) shows the locations of the fifth roots of unity.
More generally, from any particular fifth root of some number it is possible to obtain four more, by multiplying it by
q, q
2
,
q
3
, and
q
4
. These numbers are also spaced equally around a circle centered at 0. For example, the five fifth roots of 2 are shown in the right-hand figure.
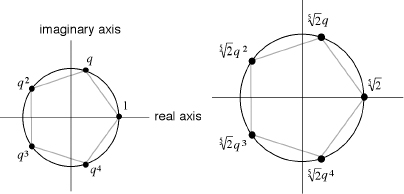
(Left) The fifth roots of unity in the complex plane. (Right) The fifth roots of two.
This was all very pretty, but it suggested something much deeper. The fifth roots of 2 can be viewed as the solutions of the equation
x
5
= 2. This equation is of the fifth degree, and it has five complex solutions, only one of which is real. Similarly, the equation
x
4
= 2 for fourth roots of 2 has four solutions, the equation for 17th roots of 2 has 17 solutions, and so on. You don't have to be a genius to spot the pattern: the number of solutions is equal to the degree of the equation.
The same seemed to apply not just to the equations for
n
th roots, but to
any algebraic equation whatsoever.
Mathematicians became convinced that within the realm of complex numbers, every equation has exactly the same number of solutions as its degree. (Technically, this statement is true only when solutions are counted according to their “multiplicity.” If this convention is not used, then the number of solutions is less than or equal to the degree.) Euler proved this property for equations of degree 2, 3, and 4, and claimed that similar methods would work in general. His ideas were plausible, but filling in the gaps turned out to be almost impossible, and even today it takes a major effort to push Euler's method to a conclusion. Nevertheless, mathematicians assumed that if they were solving an equation of some degree, they should expect to find precisely that many solutions.
As Gauss developed his ideas in number theory and analysis, he became more and more dissatisfied that no one had proved this assumption. Characteristically, he came up with a proof. It was complicated and curiously indirect: any competent mathematician could be convinced that it
was correct, but no one could guess how Gauss had come up with it in the first place. The fox of mathematics was wielding his tail with a vengeance.

The Latin title of Gauss's dissertation translates as “A new proof that every rational integral function of one variable can be resolved into real factors of the first or second degree.” Unwrapping the jargon of the period, the title asserts that every polynomial (with real coefficients) is a product of terms that are either linear or quadratic polynomials.
Gauss used the word “real” to make it clear that he was working within the traditional number system, in which negative quantities lack square roots. Nowadays we would state Gauss's theorem in a logically equivalent but simpler form: every real polynomial of degree
n
has
n
real or complex roots. But Gauss chose his terminology carefully, so that his work did not rely on the still puzzling system of complex numbers. Complex roots of a real polynomial can always be combined in pairs to yield real quadratic factors, whereas linear factors correspond to real roots. By phrasing the title in terms of these two types of factor (“factors of the first or second degree”), Gauss circumvented the contentious issue of complex numbers.
One word in the title was unjustified: “new,” which implies that there are “old” proofs. Gauss gave the
first
rigorous proof of this basic theorem in algebra. But to avoid offending illustrious predecessors who had already claimed proofsâall of them faultyâGauss presented his breakthrough as merely the latest proof, using new (that is, correct) methods.
This theorem came to be known as the Fundamental Theorem of Algebra. Gauss considered it so important that he gave four proofs in all, the last at the age of 70. He personally had no qualms about complex numbers: they played a big role in his thinking, and he subsequently developed his own explanation of their meaning. But he disliked controversy. Over the years he suppressed many of his most original ideasânon-Euclidean geometry, complex analysis, and a rigorous approach to complex numbers themselvesâbecause he did not want to attract what he referred to as “the cries of the Boeotians.”

Gauss did not confine himself to pure mathematics. Early in 1801, the Italian priest and astronomer Giuseppe Piazzi had discovered a new planet, or so he thoughtâa faint patch of light in his telescope that
moved against the background of the stars from one night to the next, a sure sign that it was a body in the solar system. It was duly given the name Ceres, but it was actually an asteroid, the first to be found. Having found the new world, Piazzi promptly lost it in the glare of the Sun. He had made so few observations that astronomers hadn't been able to work out the new body's orbit and worried that they wouldn't be able to locate it again when it emerged from behind the Sun.
This was a problem worthy of Gauss, and he set to with a will. He invented better ways to determine orbits from small numbers of observations, and predicted where Ceres would reappear. When it duly did so, Gauss's fame spread far and wide. The explorer Alexander von Humboldt asked Pierre-Simon de Laplace, an expert in celestial mechanics, to name the greatest mathematician in Germany, and got the reply “Pfaff.” When a startled Humboldt asked, “What about Gauss?” Laplace replied, “Gauss is the greatest mathematician in the world.”
Unfortunately, this newfound celebrity diverted him from pure mathematics into lengthy calculations in celestial mechanicsâgenerally felt to be a waste of his considerable talents. It's not that celestial mechanics was unimportant, but other, less able mathematicians could have done the same work. On the other hand, it also set him up for life. Gauss had been looking for a prominent position that offered the opportunity for public service, to reward his sponsor, the duke. His work on Ceres landed him the directorship of the Göttingen observatory, a post that he held for the rest of his academic life.
He married Johanna Osthoff in 1805. Writing to Bolyai, he described his new wife: “The beautiful face of a Madonna, a mirror of peace of mind and health, tender, somewhat fanciful eyes, a blameless figureâthis is one thing; a bright mind and an educated languageâthis is another; but the quiet, serene, modest and chaste soul of an angel who can do no harm to any creatureâthat is the best.” Johanna bore him two children, but in 1809 she died in childbirth, and a devastated Gauss “closed her angelic eyes in which I have found heaven for the last five years.” He became lonely and depressed, and life for him was never quite the same. He did find a new wife, Johanna's best friend Minna Waldeck, but the marriage was not terribly happy despite the birth of three more children. Gauss was always arguing with his sons and telling his daughters what to do, and the boys got so fed up that they left Europe for the United States, where they prospered.