Why Beauty is Truth (14 page)

Tartaglia had rediscovered del Ferro's method, but he suspected that Fior also knew how to solve other types of cubic and would thus have a huge advantage. Tartaglia tells us how much this prospect worried him, and how he finally cracked the remaining case shortly before the contest. Now Tartaglia had the advantage, and he promptly wiped out the unlucky Fior.

Word of the defeat spread; Cardano heard of it in Milan. At that time he was working on his algebra text. Like any true author, Cardano was determined to include the latest discoveries, for without them his book would be obsolete before it was even published. So Cardano approached Tartaglia, hoping to wheedle the secret out of him and put it in
The Great Art.
Tartaglia refused, saying that he intended to write his own book.

Eventually, however, Cardano's persistence paid off, and Tartaglia divulged the secret. Did he
really
make Cardano swear to keep it hidden, knowing that a textbook was in the offing? Or did he succumb to Cardano's blandishments and then regret it?

There is no doubt that he was extremely angry when
The Great Art
appeared. Within a year he had published a book,
Diverse Questions and Inventions
, which laid into Cardano in no uncertain terms. He included all of the correspondence between them, supposedly exactly as written.

In 1574, Ferrari came to the support of his master by issuing a
cartello
—a challenge to a learned dispute on any topic Tartaglia cared to name. He even offered a prize of 200 scudi for the winner. And he made his opinions very clear: “This I have proposed to make known, that you have written things which falsely and unworthily slande . . . Signor Girolamo, compared to whom you are hardly worth mentioning.”

Ferrari sent copies of the
cartello
to numerous Italian scholars and public figures. Within nine days, Tartaglia responded with his own statement of facts, and the two mathematicians ended up by exchanging twelve
cartelli
between them over a period of eighteen months. The dispute seems to have followed the standard rules for a genuine duel. Tartaglia, who had been insulted by Ferrari, was allowed the choice of weapons—the selection of topics to be debated. But he kept asking to debate Cardano rather than his challenger, Ferrari.

Ferrari kept his temper under control and pointed out that in any case it had been del Ferro, not Tartaglia, who had solved the cubic to begin with.
Since del Ferro had made no fuss about Tartaglia's unjustified claim of credit, why wasn't Tartaglia willing to behave likewise? It was a good point, and Tartaglia may have recognized that, because he considered withdrawing from the contest. However, he didn't, and one possible reason was the city fathers of Brescia, his hometown. Tartaglia was after a lectureship there, and the local dignitaries may have wanted to see how he acquitted himself.

At any rate, Tartaglia agreed to the debate, which was held in a Milanese church before large crowds in August 1548. No record of the proceedings is known, save for a few indications by Tartaglia, who said that the meeting ceased when suppertime approached. This hints that the debate may not have been especially gripping. It seems, though, that Ferrari won handily, because afterward he was offered some plum positions, accepted the post of tax assessor to the governor of Milan, and soon became very rich. Tartaglia, on the other hand, never claimed to have won the debate, failed to get the Brescia job, and descended into bitter recrimination.

Unknown to Tartaglia, Cardano and Ferrari had an entirely different line of defense, for they had visited Bologna and inspected del Ferro's papers. These included the first genuine solution of the cubic, and in later years they both insisted that the source of the material included in
The Great Art
was del Ferro's original writings, not Tartaglia's confidence to Cardano. The reference to Tartaglia was included merely to record how Cardano himself heard of del Ferro's work.

There is a final twist to the tale. Soon after the second edition of
The Great Art
was published, in 1570, Cardano was imprisoned by the Inquisition. The reason may have been something that had previously seemed entirely innocent: not the content of the book, but its dedication. Cardano had chosen to dedicate it to the relatively obscure intellectual Andreas Osiander, a minor figure in the Reformation but one strongly suspected of being the author of an anonymous preface to Nicolaus Copernicus's
On the Revolutions of the Heavenly Spheres
, the first book to propose that the planets go around the Sun, not the Earth. The Church considered this view heretical, and in 1600 it burned Giordano Bruno alive for maintaining it—hanging him upside down from a stake, naked and gagged, in a Roman market square. In 1616, and again in 1633, it gave Galileo a lot of grief, for the same reason, but by then the Inquisition was content to put him under house arrest.

To appreciate what Girolamo and his compatriots achieved, we must revisit the Babylonian tablet that explains how to solve quadratics. If we follow the recipe and express the calculation steps in modern symbolism, we see that in effect the Babylonian scribe was saying that the solution to a quadratic equation
x
²
–
ax
=
b
is

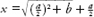
This is equivalent to the formula that every school student used to learn by heart, and that nowadays is found in every formula book.

The Renaissance solution of the cubic equation is similar but more elaborate. In modern symbols it looks like this: Suppose that
x
³
+
ax
=
b.
Then

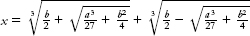
As formulas go, this one is relatively simple (believe me!), but you need to develop a lot of algebraic ideas before it can be so described. It is by far the most complicated formula we will look at, and it uses all three types of symbol that I have introduced: letters, raised numbers, and the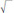
sign, as well as both square roots and cube roots. You don't need to understand this formula, and you certainly don't need to calculate it. But you need to appreciate its general shape. First, some terminology that will prove very useful as we proceed.

An algebraic expression like 2
x
⁴
– 7
x
³
– 4
x
²
+ 9 is called a
polynomial
, which means “many terms.” Such expressions are formed by adding various powers of the unknown. The numbers 2, –7, –4, and 9, which multiply the powers, are called
coefficients.
The highest power of the unknown that occurs is called the
degree
of the polynomial, so this polynomial has degree 4. There are special names for polynomials of low degree (1 through 6): linear, quadratic, cubic, quartic, quintic, and sextic. The solutions of the associated equation 2
x
⁴
– 7
x
³
– 4
x
²
+ 9 = 0 are called the
roots
of the polynomial.

Now we can dissect Cardano's formula. It is built from the coefficients
a
and
b
, employing some additions, subtractions, multiplications, and divisions (but only by certain integers, namely 2, 4, and 27). The esoteric aspects are of two kinds: There is a square root—in fact the same square root occurs in two places, but one is added while the other is subtracted.
Finally, there are two cube roots, and these are the cube roots of quantities that involve the square roots. So aside from harmless operations of algebra (by which I mean those that merely shuffle the terms around), the skeleton of the solution is, “Take a square root, then a cube root; do this again; add the two.”

That's all we will need. But I don't think we can get away with less.

What the Renaissance mathematicians initially failed to grasp, but later generations soon realized, is that this formula is not just a solution to one type of cubic. It is a complete solution to
all
types, give or take some straightforward algebra. For a start, if the cube term is, say, 5
x
³
instead of
x
³
, you can just divide the entire equation by 5—the Renaissance mathematicians were certainly smart enough to spot that. A more subtle idea, which required a quiet revolution in how we think of numbers, is that by allowing the coefficients
a
and
b
to be
negative
if necessary, we can avoid fruitless distinctions among cases. Finally, there is a purely algebraic trick: if the equation involves the square of the unknown, you can always get rid of it—you replace
x
by
x
plus a carefully chosen constant, and if you do it right, the square term miraculously disappears. Again, it helps here if you stop worrying whether numbers are positive or negative. Finally, the Renaissance mathematicians worried about terms that were entirely missing, but to modern eyes the remedy is obvious: such a term is not actually
missing
, it just has coefficient zero. The same formula works.