Why Beauty is Truth (11 page)
Read Why Beauty is Truth Online
Authors: Ian Stewart

Each listed term would have a positive numerical coefficient. You may be wondering why this list does not include cases like
cube + square = side
The reason is that in these cases we can divide both sides of the equation by the unknown, reducing it to a quadratic.

Omar did not entirely invent his solutions but instead built on earlier Greek methods for solving various types of cubic equation using conic sections. He developed these ideas systematically, and solved all fourteen types of cubic by such methods. Previous mathematicians, he noted, had discovered solutions of various cases, but these methods were all very special and each case was tackled by a different construction; no one before him had worked out the whole extent of possible cases, let alone found solutions to them. “Me, on the contraryâI have never ceased to wish to make known, with exactitude, all of the possible cases, and to distinguish among each of the cases the possible and impossible ones.” By “impossible” he meant “having no
positive
solution.”
To give a flavor of his work, here is how he solved “A cube, some sides, and some numbers are equal to some squares,” which we would write as
x
3
+
bx
+
c
=
ax
2
.
(Since we don't care about positive versus negative, we would probably move the right-hand term to the other side and change
a
to â
a
as well:
x
3
â
ax
2
+
bx
+
c
= 0).
Omar instructs his readers to carry out the following sequence of steps. (1) Draw three lines of lengths
c
/
b
,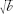 , and
, and
a
, with a right angle. (2) Draw a semicircle whose diameter is the horizontal line. Extend the vertical line to cut it. If the solid vertical line has length
d
, make the solid horizontal line have length
c
d
/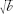 . (3) Draw a hyperbola (solid line) whose asymptotes (those special straight lines that the curves approach) are the shaded lines,
. (3) Draw a hyperbola (solid line) whose asymptotes (those special straight lines that the curves approach) are the shaded lines,
passing through the point just constructed. (4) Find where the hyperbola cuts the semicircle. Then the lengths of the two solid lines, marked
x
, are both (positive) solutions of the cubic.
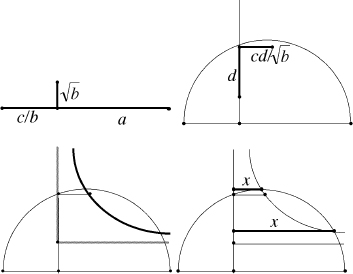
Omar Khayyám's solution of a cubic equation.
The details, as usual, matter much less than the overall style. Carry out various Euclidean constructions with ruler and compass, throw in a hyperbola, carry out some more Euclidean constructionsâdone.
Omar gave similar constructions to solve each of his fourteen cases, and proved them correct. His analysis has a few gaps: the points required in his construction sometimes fail to exist when the sizes of the coefficients
a, b, c
are unsuitable. In the construction above, for example, the hyperbola may not meet the semicircle at all. But aside from these quibbles, he did an impressive and very systematic job.
Some of the imagery in Omar's poetry is mathematical and seems to allude to his own work, in the self-deprecatory tone that we find throughout:
For “Is” and “Is-Not,” though with Rule and Line
And “Up-And-Down” by logic I define,
Of all that one should care to fathom, I
Was never deep in anything butâWine.
One especially striking stanza reads:
We are no other than a moving row
Of Magic Shadow-shapes that come and go
Round with the Sun-illumined Lantern held
In midnight by the Master of the Show.
This recalls Plato's celebrated allegory of shadows on a cave wall. It serves equally well as a description of the symbolic manipulations of algebra, and the human condition. Omar was a gifted chronicler of both.
THE GAMBLING SCHOLAR
“I
swear to you, by God's holy Gospels, and as a true man of honor, not only never to publish your discoveries, if you teach me them, but I also promise you, and I pledge my faith as a true Christian, to note them down in code, so that after my death no one will be able to understand them.”
This solemn oath wasâallegedlyâsworn in 1539.
Renaissance Italy was a hotbed of innovation, and mathematics was no exception. In the iconoclastic spirit of the age, Renaissance mathematicians were determined to overcome the limitations of classical mathematics. One of them had solved the mysterious cubic. Now he was accusing another of stealing his secret.
The irate mathematician was Niccolo Fontana, nicknamed “Tartaglia,” the stammerer. The alleged thief of his intellectual property was a mathematician, a doctor, an incorrigible rogue, and an inveterate gambler. His name was Girolamo Cardano, aka Jerome Cardan. Around 1520, Girolamo, a true prodigal son, had worked his way through his father's legacy. Broke, he turned to gambling as a source of finance, putting his mathematical abilities to effective use in assessing the chances of winning. He kept dubious company; once, when he suspected another player of cheating, he slashed the man's face with a knife.
They were hard times, and Girolamo was a hard man. He was also a highly original thinker, and he wrote one of the most famous and influential algebra texts in history.

We know a lot about Girolamo because in 1575 he told us all about himself in
The Book of My Life.
It begins thus:
This Book of My Life I am undertaking to write after the example of Antoninus the Philosopher, acclaimed the wisest and best of men, knowing well that no accomplishment of mortal man is perfect, much less safe from calumny; yet aware that none, of all ends which man may attain, seems more pleasing, none more worthy than recognition of the truth.
   No word, I am ready to affirm, has been added to give savor of vainglory, or for sake of mere embellishment; rather, as far as possible, mere experiences were collected, events of which my pupils . . . had some knowledge, or in which they took part. These brief cross-sections of my history were in turn written down by me in narrative form to become this my book.
Like many mathematicians of the period, Girolamo practiced astrology, and he notes the astrological circumstances surrounding his birth:
Although various abortive medicinesâas I have heardâwere tried in vain, I was normally born on the 24th day of September in the year 1500, when the first hour of the night was more than half run, but less than two thirds . . . Mars was casting an evil influence on each luminary because of the incompatibility of their positions, and its aspect was square to the moon.
   . . . I could easily have been a monster, except for the fact that the place of the preceding conjunction had been 29° in Virgo, over which Mercury is the ruler. And neither this planet nor the position of the moon or of the ascendant is the same, nor does it apply to the second decanate of Virgo; consequently I ought to have been a monster, and indeed was so near it that I came forth literally torn from my mother's womb.
   So I was born, or rather taken by violent means from my mother; I was almost dead. My hair was black and curly. I was revived in a bath of warm wine which might have been fatal to any other child. My mother had been in labor for three entire days, and yet I survived.
One chapter of
The Book of My Life
lists the books Girolamo wrote, and the first on the list is
The Great Art
, one of three “treatises in mathematics” that he mentions. He also wrote on astronomy, physics, morality, gemstones, water, medicine, divination, and theology.
Only
The Great Art
plays a part in our tale. Its subtitle,
The Rules of Algebra
, explains why. In it, Girolamo assembled methods for solving not just the quadratic equation, known to the Babylonians, but newly discovered solutions for cubic and quartic equations. Unlike Khayyám's solutions, which depended on the geometry of conics, those in
The Great Art
are purely algebraic.
