Why Beauty is Truth (15 page)
Read Why Beauty is Truth Online
Authors: Ian Stewart

Problem solved?
Not quite. I lied.
Here is where I lied. I said that Cardano's formula solves
all
cubics. There is a sense in which that's not true, and it turned out to be important. I didn't tell a very bad lie, though, because it all depends on what you mean by “solve.”
Cardano himself spotted the difficulty, which says a lot for his attention to detail. Cubics typically have either three solutions (fewer if we exclude negative numbers) or one. Cardano noticed that when there are three solutionsâsay 1, 2, and 3âthe formula does not seem to yield those solutions in any sensible way. Instead, the square root in the formula contains a negative number.
Specifically, Cardano noted that the cubic
x
3
= 15
x
+ 4 has the obvious solution
x
= 4. But when he tried out Tartaglia's formula, it led to the “answer”
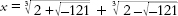
which seemed meaningless.
Among European mathematicians in those days, few brave souls were willing to contemplate negative numbers. Their Eastern counterparts had come to terms with negative quantities much earlier. In India, the Jains developed a rudimentary concept of negative quantities as early as 400, and in 1200 the Chinese system of “counting rods” used red rods for positive numbers and black rods for negative onesâthough only in certain limited contexts.
If negative numbers were a puzzle, their square roots had to be even more baffling. The difficulty is that the square of either a positive or a negative number is always
positive
âI won't explain why here, but it is the only choice that makes the laws of algebra work consistently. So even if you are happy using negative numbers, it seems that you have to accept that they cannot have sensible square roots. Any algebraic expression involving the square root of a negative quantity must therefore be nonsense.
And yet Tartaglia's formula led Cardano to just such an expression. It was worrying in the extreme that in cases in which you
knew
the solution by some other route, the formula seemed not to produce it.
In 1539 a worried Cardano raised the matter with Tartaglia:
I have sent to enquire after the solution to various problems for which you have given me no answer, one of which concerns the cube equal to an unknown plus a number. I have certainly grasped this rule, but when the cube of one-third of the coefficient of the unknown is greater in value than the square of one-half of the number, then, it appears, I cannot make it fit into the equation.
Here Cardano is describing exactly the condition for the square root to be that of a negative number. It is clear that he had an excellent grasp of the whole business and had spotted a snag. It is less clear whether Tartaglia had a comparable level of understanding of his own formula,
because his response was, “you have not mastered the true way of solving problems of this kind . . . Your methods are totally false.”
Possibly Tartaglia was merely being deliberately unhelpful. Or possibly he did not see what Cardano was getting at. At any rate, Cardano had put his finger on a puzzle that would exercise the combined intellects of the world's mathematicians for the next 250 years.

Even in Renaissance times, there were hints that something important might be going on. The same issue arose in another problem discussed in
The Great Art
, to find two numbers whose sum is 10 and whose product is 40. This led to the “solution” 5 +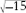 and 5 â
and 5 â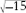 . Cardano noticed that if you ignored the question of what the square root of minus fifteen
. Cardano noticed that if you ignored the question of what the square root of minus fifteen
meant
, and just pretended it worked like any other square root, then you could check that these “numbers” actually fit the equation. When you added them, the square roots canceled out, and the two 5's added to 10, as required. When you multiplied them, you got 5
2
â (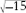 )
)
2
, which equals 25 + 15, which is 40. Cardano did not know what to make of this strange calculation. “So,” he wrote, “progresses arithmetic subtlety, the end of which is as refined as it is useless.”
In his
Algebra
of 1572, Rafaele Bombelli, the son of a Bolognese wool merchant, noticed that similar calculations, manipulating the “imaginary” roots as if they were genuine numbers, could convert the weird formula for Cardano's puzzling cubic into the correct answer,
x
= 4. He wrote the book to fill in some spare time while he was reclaiming marshland for the Apostolic Camera, the Pope's legal and financial department. Bombelli noticed that
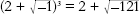
and
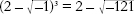
so the sum of the two strange cube roots becomes
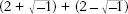
which equals 4. The meaningless root was somehow meaningful, and it gave the right answer. Bombelli was probably the first mathematician to realize that you could carry out algebraic manipulations with square roots of negative numbers and get usable results. This was a big hint that such numbers had a sensible interpretation, but it didn't seem to indicate what that interpretation was.

The mathematical high point of Cardano's book was not the cubic but the quartic. His student Ferrari managed to extend Tartaglia and del Ferro's methods to equations that contain the fourth power of the unknown. Ferrari's formula involves only square roots and cube rootsâa fourth root is just the square root of a square root, so those are not needed.