A Briefer History of Time (6 page)

This behavior of the universe could have been predicted from Newton’s theory of gravity at any time in the nineteenth, the eighteenth, or even the late seventeenth century. Yet so strong was the belief in a static universe that it persisted into the early twentieth century. Even Einstein, when he formulated the general theory of relativity in 1915, was so sure that the universe had to be static that he modified his theory to make this possible by introducing a fudge factor, called the cosmological constant, into his equations. The cosmological constant had the effect of a new "antigravity" force, which, unlike other forces, did not come from any particular source but was built into the very fabric of space-time. As a result of this new force, space-time had an inbuilt tendency to expand. By adjusting the cosmological constant, Einstein could adjust the strength of this tendency. He found he could adjust it to exactly balance the mutual attraction of all the matter in the universe, so a static universe would result. He later disavowed the cosmological constant, calling this fudge factor his "greatest mistake." As we’ll soon see, today we have reason to believe that he might have been right to introduce it after all. But what must have disappointed Einstein was that he had allowed his belief in a static universe to override what his theory seemed to be predicting: that the universe is expanding. Only one man, it seems, was willing to take this prediction of general relativity at face value. While Einstein and other physicists were looking for ways of avoiding general relativity’s nonstatic universe, the Russian physicist and mathematician Alexander Friedmann instead set about explaining it.
Friedmann made two very simple assumptions about the universe: that the universe looks identical in whichever direction we look, and that this would also be true if we were observing the universe from anywhere else. From these two ideas alone, Friedmann showed, by solving the equations of general relativity, that we should not expect the universe to be static. In fact, in 1922, several years before Edwin Hubble’s discovery, Friedmann predicted exactly what Hubble later found!
The assumption that the universe looks the same in every direction is clearly not exactly true in reality. For example, as we have noted, the other stars in our galaxy form a distinct band of light across the night sky, called the Milky Way. But if we look at distant galaxies, there seems to be more or less the same number of them in every direction. So the universe does appear to be roughly the same in every direction, provided we view it on a large scale compared to the distance between galaxies, and ignore the differences on small scales. Imagine standing in a forest in which the trees are growing in random locations. If you look in one direction, you may see the nearest tree at a distance of one meter. In another direction, the nearest tree might be three meters away. In a third direction, you might see a clump of trees at two meters. It doesn’t seem as if the forest looks the same in every direction, but if you were to take into account all the trees within a one-mile radius, these kinds of differences would average out and you would find that the forest is the same in whichever direction you look.
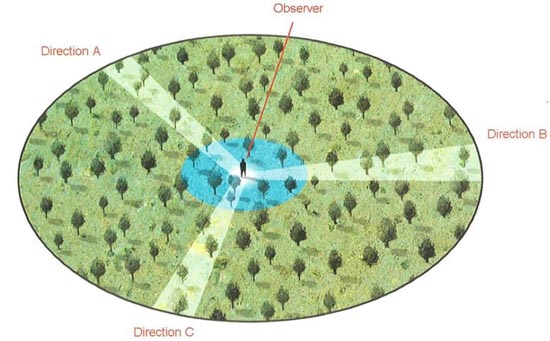
Isotropic Forest
Even if the trees in a forest are uniformly distributed, nearby trees may appear bunched. Similarly, the universe does not look uniform in our local neighborhood, yet on large scales our view appears identical in whichever direction we look.
For a long time, the uniform distribution of stars was sufficient justification for Friedmann’s assumption—as a rough approximation to the real universe. But more recently a lucky accident uncovered another respect in which Friedmann’s assumption is in fact a remarkably accurate description of our universe. In 1965, two American physicists at the Bell Telephone Laboratories in New Jersey, Arno Penzias and Robert Wilson, were testing a very sensitive microwave detector. (Recall that microwaves are just like light waves, but with a wavelength of around a centimeter.) Penzias and Wilson were worried when they found that their detector was picking up more noise than it ought to. They discovered bird droppings in their detector and checked for other possible malfunctions, but they soon ruled these out. The noise was peculiar in that it remained the same day and night and throughout the year, even though the earth was rotating on its axis and orbiting around the sun. Since the earth’s rotation and orbit pointed the detector in different directions in space, Penzias and Wilson concluded that the noise was coming from beyond the solar system and even from beyond the galaxy. It seemed to be coming equally from every direction in space. We now know that in whichever direction we look, this noise never varies by more than a tiny fraction, so Penzias and Wilson had unwittingly stumbled across a striking example of Friedmann’s first assumption that the universe is the same in every direction.
What is the origin of this cosmic background noise? At roughly the same time as Penzias and Wilson were investigating noise in their detector, two American physicists at nearby Princeton University, Bob Dicke and Jim Peebles, were also taking an interest in microwaves. They were working on a suggestion, made by George Gamow (once a student of Alexander Friedmann), that the early universe should have been very hot and dense, glowing white hot. Dicke and Peebles argued that we should still be able to see the glow of the early universe, because light from very distant parts of it would only just be reaching us now. However, the expansion of the universe meant that this light should be so greatly red-shifted that it would appear to us now as microwave radiation, rather than visible light. Dicke and Peebles were preparing to look for this radiation when Penzias and Wilson heard about their work and realized that they had already found it. For this, Penzias and Wilson were awarded the Nobel Prize in 1978 (which seems a bit hard on Dicke and Peebles, not to mention Gamow).
At first sight, all this evidence that the universe appears the same whichever direction we look in might seem to suggest there is something distinctive about our place in the universe. In particular, it might seem that if we observe all other galaxies to be moving away from us, then we must be at the center of the universe. There is, however, an alternative explanation: the universe might look the same in every direction as seen from any other galaxy too. This, as we have seen, was Friedmann’s second assumption.
We have no scientific evidence for or against that second assumption. Centuries ago, the church would have considered the assumption heresy, since church doctrine stated that we do occupy a special place at the center of the universe. But today we believe Friedmann’s assumption for almost the opposite reason, a kind of modesty: we feel it would be most remarkable if the universe looked the same in every direction around us but not around other points in the universe!
In Friedmann’s model of the universe, all the galaxies are moving directly away from each other. The situation is rather like a balloon with a number of spots painted on it being steadily blown up. As the balloon expands, the distance between any two spots increases, but there is no spot that can be said to be the center of the expansion. Moreover, as the radius of the balloon steadily increases, the farther apart the spots on the balloon, the faster they will be moving apart. For example, suppose that the radius of the balloon doubles in one second. Two spots that were previously one centimeter apart will now be two centimeters apart (as measured along the surface of the balloon), so their relative speed is one centimeter per second. On the other hand, a pair of spots that were separated by ten centimeters will now be separated by twenty, so their relative speed will be ten centimeters per second. Similarly, in Friedmann’s model the speed at which any two galaxies are moving apart is proportional to the distance between them, so he predicted that the red shift of a galaxy should be directly proportional to its distance from us, exactly as Hubble found. Despite the success of his model and his prediction of Hubble’s observations, Friedmann’s work remained largely unknown in the West until similar models were discovered in 1935 by the American physicist Howard Robertson and the British mathematician Arthur Walker, in response to Hubble’s discovery of the uniform expansion of the universe.
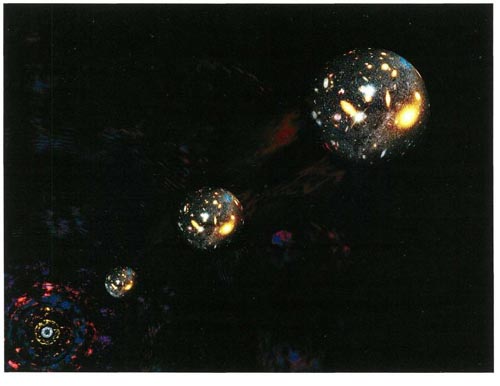
The Expanding Balloon Universe
As a result of the expansion of the universe, all galaxies are moving directly away from each other Over time, like spots on an inflating balloon, galaxies that are farther apart increase their separation more than nearer galaxies Hence, to an observer in any given galaxy, the more distant a galaxy is, the faster it appears to be moving
Friedmann derived only one model of the universe. But if his assumptions are correct, there are actually three possible types of solutions to Einstein’s equations, that is, three different kinds of Friedmann models—and three different ways the universe can behave.
In the first kind of solution (which Friedmann found), the universe is expanding sufficiently slowly that the gravitational attraction between the different galaxies causes the expansion to slow down and eventually to stop. The galaxies then start to move toward each other, and the universe contracts. In the second kind of solution, the universe is expanding so rapidly that the gravitational attraction can never stop it, though it does slow it down a bit. Finally, there is a third kind of solution, in which the universe is expanding only just fast enough to avoid collapse. The speed at which the galaxies are moving apart gets smaller and smaller, but it never quite reaches zero.
A remarkable feature of the first kind of Friedmann model is that in it the universe is not infinite in space, but neither does space have any boundary. Gravity is so strong that space is bent round onto itself. This is rather like the surface of the earth, which is finite but has no boundary. If you keep traveling in a certain direction on the surface of the earth, you never come up against an impassable barrier or fall over the edge, and you eventually come back to where you started. In this model, space is just like this, but with three dimensions instead of two for the earth’s surface. The idea that you could go right round the universe and end up where you started makes good science fiction, but it doesn’t have much practical significance, because it can be shown that the universe would collapse to zero size before you could get around. It is so large, you would need to travel faster than light in order to end up where you started before the universe came to an end—and that is not allowed! Space is also curved in the second Friedmann model, though in a different way. Only the third Friedmann model corresponds to a universe whose large-scale geometry is flat (though space is still curved, or warped, in the vicinity of massive objects).
Which Friedmann model describes our universe? Will the universe eventually stop expanding and start contracting, or will it expand forever?
It turns out the answer to this question is more complicated than scientists first thought. The most basic analysis depends on two things: the present rate of expansion of the universe, and its present average density (the amount of matter in a given volume of space). The faster the current rate of expansion, the greater the gravitational force required to stop it, and thus the greater the density of matter needed. If the average density is greater than a certain critical value (determined by the rate of expansion), the gravitational attraction of the matter in the universe will succeed in halting its expansion and cause it to collapse—corresponding to the first Friedmann model. If the average density is less than the critical value, there is not enough gravitational pull to stop the expansion, and the universe will expand forever— corresponding to Friedmann’s second model. And if the average density of the universe is exactly the critical number, then the universe will forever slow its expansion, ever more gradually approaching, but not ever reaching, a static size. This corresponds to the third Friedmann model.
So which is it? We can determine the present rate of expansion by measuring the velocities at which other galaxies are moving away from us, using the Doppler effect. This can be done very accurately. However, the distances to the galaxies are not very well known because we can measure them only indirectly. So all we know is that the universe is expanding by between 5 percent and 10 percent every billion years. Our uncertainty about the present average density of the universe is even greater. Still, if we add up the masses of all the stars that we can see in our galaxy and other galaxies, the total is less than one hundredth of the amount required to halt the expansion of the universe, even for the lowest estimate of the rate of expansion.