A Briefer History of Time (5 page)

How would this situation differ if the rocket ship were resting on earth, under the influence of gravity, instead of floating freely out in space? According to Newton’s theory, gravity has no effect on this situation. If the observer on the ceiling sends signals one second apart, the observer will receive them one second apart. But the principle of equivalence does not make the same prediction. We can see what happens, that principle tells us, by considering the effect of uniform acceleration instead of the effect of gravity. This is an example of the way Einstein used the principle of equivalence to create his new theory of gravity.
So let’s now suppose the rocket ship is accelerating. (We will imagine that it is accelerating slowly, so we don’t approach the speed of light!) Since the rocket ship is moving upward, the first signal will have less distance to travel than before and so will arrive sooner than one second later. If the rocket ship were moving at a constant speed, the second signal would arrive exactly the same amount of time sooner, so the time between the two signals would remain one second. But due to the acceleration, the rocket ship will be moving even faster when the second signal is sent than it was when the first signal was sent, so the second signal will have even less distance to traverse than the first and will arrive in even less time. The observer on the floor will therefore measure less than one second between the signals, disagreeing with the ceiling observer, who claims to have sent them exactly one second apart.
This is probably not startling in the case of the accelerating rocket ship—after all, we just explained it! But remember, the principle of equivalence says that it also applies to a rocket ship at rest in a gravitational field. That means that even if the rocket ship is not accelerating but, say, is sitting on a launching pad on the earth’s surface, if the ceiling observer sends signals toward the floor at intervals of one each second (according to his clock), the floor observer will receive the signals at shorter intervals (according to his clock). That is startling!
You might still ask whether this means that gravity changes time, or whether it merely ruins clocks. Suppose the floor observer climbs up to the ceiling, where he and his partner compare their clocks. They are identical clocks, and sure enough, both observers will find that they now agree on the length of a second. There is nothing wrong with the floor observer’s clock: it measures the local flow of time, wherever it happens to be. So just as special relativity tells us that time runs differently for observers in relative motion, general relativity tells us that time runs differently for observers at different heights in a gravitational field. According to general relativity, the floor observer measured less than one second between signals because time moves more slowly closer to the earth’s surface. The stronger the field, the greater this effect. Newton’s laws of motion put an end to the idea of absolute position in space. We have now seen how the theory of relativity gets rid of absolute time.
This prediction was tested in 1962, using a pair of very accurate clocks mounted at the top and bottom of a water tower. The clock at the bottom, which was nearer the earth, was found to run slower, in exact agreement with general relativity. The effect is a small one-a clock on the surface of the sun would gain only about a minute a year as compared to one on the surface of the earth. Yet with the advent of very accurate navigation systems based on signals from satellites, the difference in the speed of clocks at different heights above the earth is now of considerable practical importance. If you ignored the predictions of general relativity, the position that you calculated would be wrong by several miles!
Our biological clocks are equally affected by these changes in the flow of time. Consider a pair of twins. Suppose that one twin goes to live on the top of a mountain while the other stays at sea level. The first twin would age faster than the second. Thus, if the; met again, one would be older than the other. In this case, the difference in ages would be very small, but it would be much larger if one of the twins went for a long trip in a spaceship in which he accelerated to nearly the speed of light. When he returned, he would be much younger than the one who stayed on earth. This is known as the twins paradox, but it is a paradox only if you have the idea of absolute time at the back of your mind. In the theory of relativity there is no unique absolute time; instead, each individual has his own personal measure of time that depends on where he is and how he is moving.
Before 1915, space and time were thought of as a fixed arena in which events took place but which was not affected by what happened in it. This was true even of the special theory of relativity. Bodies moved, forces attracted and repelled, but time and space simply continued unaffected. It was natural to think that space and time went on forever. The situation, however, is quite different in the general theory of relativity. Space and time are now dynamic quantities: when a body moves or a force acts, it affects the curvature of space and time—and in turn the structure of space-time affects the way in which bodies move and forces act. Space and time not only affect but also are affected by everything that happens in the univ erse. Just as we cannot talk about events in the universe without the notions of space and time, so in general relativity it became meaningless to talk about space and time outside the limits of the universe. In the decades following 1915, this new understanding of space and time was to revolutionize our view of the universe. As we will see, the old idea of an essentially unchanging universe that could have existed forever, and could continue to exist forever, was replaced by the notion of a dynamic, expanding universe that seemed to have begun a finite time ago and which might end at a finite time in the future.
7
THE EXPANDING UNIVERSE
IF YOU LOOK AT THE SKY on a clear, moonless night, the brightest objects you see are likely to be the planets Venus, Mars, Jupiter, and Saturn. There will also be a very large number of stars, which are just like our own sun but much farther from us. Some of these fixed stars do, in fact, appear to change very slightly their positions relative to each other as the earth orbits around the sun. They are not really fixed at all! This is because they are comparatively near to us. As the earth goes around the sun, we see the nearer stars from different positions against the background of more distant stars. The effect is the same one you see when you are driving down an open road and the relative positions of nearby trees seem to change against the background of whatever is on the horizon. The nearer the trees, the more they seem to move. This change in relative position is called parallax. (See illustration on page 52.) In the case of stars, it is fortunate, because it enables us to measure directly the distance of these stars from us.
As we mentioned in Chapter 1, the nearest star, Proxima Centauri, is about four light-years, or twenty-three million million miles, away. Most of the other stars that are visible to the naked eye lie within a few hundred light-years of us. Our sun, for comparison, is a mere eight light-minutes away! The visible stars appear spread all over the night sky but are particularly concentrated in one band, which we call the Milky Way. As long ago as 1750, some astronomers were suggesting that the appearance of the Milky Way could be explained if most of the visible stars lie in a single disklike configuration, one example of what we now call a spiral galaxy. Only a few decades later, the astronomer Sir William Herschel confirmed this idea by painstakingly cataloguing the positions and distances of vast numbers of stars. Even so, this idea gained complete acceptance only early in the twentieth century We now know that the Milky Way-our galaxy—is about one hundred thousand light-years across and is slowly rotating; the stars in its spiral arms orbit around its center about once every several hundred million years. Our sun is just an ordinary, average-sized yellow star near the inner edge of one of the spiral arms. We have certainly come a long way since Aristotle and Ptolemy, when we thought that the earth was the center of the universe!
Our modern picture of the universe dates back only to 1924, when the American astronomer Edwin Hubble demonstrated that the Milky Way was not the only galaxy. He found, in fact, many others, with vast tracts of empty space between them. In order to prove this, Hubble needed to determine the distances from the earth to the other galaxies. But these galaxies were so far away that, unlike nearby stars, their positions really do appear fixed. Since Hubble couldn’t use the parallax on these galaxies, he was forced to use indirect methods to measure their distances. One obvious measure of a star’s distance is its brightness. But the apparent brightness of a star depends not only on its distance but also on how much light it radiates (its luminosity). A dim star, if near enough, will outshine the brightest star in any distant galaxy. So in order to use apparent brightness as a measure of its distance, we must know a star’s luminosity.
The luminosity of nearby stars can be calculated from their apparent brightness because their parallax enables us to know their distance.

Parallax
Whether you are moving down a road or through space, the relative position of nearer and farther objects changes as you go A measure of that change can be used to determine the relative distance of the objects
Hubble noted that these nearby stars could be classified into certain types by the kind of light they give off. The same type of stars always had the same luminosity. He then argued that if we found these types of stars in a distant galaxy, we could assume that they had the same luminosity as the similar stars nearby. With that information, we could calculate the distance to that galaxy. If we could do this for a number of stars in the same galaxy and our calculations always gave the same distance, we could be fairly confident of our estimate. In this way, Hubble worked out the distances to nine different galaxies.
Today we know that stars visible to the naked eye make up only a minute fraction of all the stars. We can see about five thousand stars, only about .0001 percent of all the stars in just our own galaxy, the Milky Way. The Milky Way itself is but one of more than a hundred billion galaxies that can be seen using modern telescopes—and each galaxy contains on average some one hundred billion stars. If a star were a grain of salt, you could fit all the stars visible to the naked eye on a teaspoon, but all the stars in the universe would fill a ball more than eight miles wide.
Stars are so far away that they appear to us to be just pinpoints of light. We cannot see their size or shape. But, as Hubble noticed, there are many different types of stars, and we can tell them apart by the color of their light. Newton discovered that if light from the sun passes through a triangular piece of glass called a prism, it breaks up into its component colors as in a rainbow. The relative intensities of the various colors emitted by a given source of light are called its spectrum. By focusing a telescope on an individual star or galaxy, one can observe the spectrum of the light from that star or galaxy.
One thing this light tells us is temperature. In 1860, the German physicist Gustav Kirchhoff realized that any material body, such as a star, will give off light or other radiation when heated, just as coals glow when they are heated. The light such glowing objects give off is due to the thermal motion of the atoms within them. It is called blackbody radiation (even though the glowing objects are not black). The spectrum of blackbody radiation is hard to mistake: it has a distinctive form that varies with the temperature of the body. The light emitted by a glowing object is therefore like a thermometer reading. The spectrum we observe from different stars is always in exactly this form: it is a postcard of the thermal state of that star.

Stellar Spectrum
By analyzing the component colors of starlight, one can determine both the temperature of a star and the composition of its atmosphere.
If we look more closely, starlight tells us even more. We find that certain very specific colors are missing, and these missing colors may vary from star to star. Since we know that each chemical element absorbs a characteristic set of very specific colors, by matching these to those that are missing from a star’s spectrum we can determine exactly which elements are present in that star’s atmosphere.

Blackbody Spectrum
All objects-not just stars-emit radiation resulting from the thermal motion of the objects’ microscopic constituents The distribution of frequencies in this radiation is characteristic of an object’s temperature
In the 1920s, when astronomers began to look at the spectra of stars in other galaxies, they found something most peculiar: there were the same characteristic patterns of missing colors as for stars in our own galaxy, but they were all shifted toward the red end of the spectrum by the same relative amount.
To physicists, the shifting of color or frequency is known as the Doppler effect. We are all familiar with it in the realm of sound. Listen to a car passing on the road: as it approaches, its engine-or its horn-sounds at a higher pitch, and after it passes and is moving away, it sounds at a lower pitch. The sound of its engine or horn is a wave, a succession of crests and troughs. When a car is racing toward us, it will be progressively nearer to us as it emits each successive wave crest, so the distance between wave crests—the wavelength of the sound—will be smaller than if the car were stationary. The smaller the wavelength, the more of these fluctuations reach our ear each second, and the higher the pitch, or frequency, of the sound. Correspondingly, if the car is moving away from us, the wavelength will be greater and the waves will reach our ear with a lower frequency The faster the car is moving, the greater the effect, so we can use the Doppler effect to measure speed. The behavior of light or radio waves is similar. Indeed, the police make use of the Doppler effect to measure the speed of cars by measuring the wavelength of pulses of radio waves reflected off them.
As we noted in Chapter 5, the wavelength of visible light is extremely small, ranging from forty- to eighty-millionths of a centimeter. The different wavelengths of light are what the human eye sees as different colors, with the longest wavelengths appearing at the red end of the spectrum and the shortest wavelengths at the blue end. Now imagine a source of light at a constant distance from us, such as a star, emitting waves of light at a constant wavelength. The wavelength of the waves we receive will be the same as the wavelength at which they are emitted. Then suppose that the source starts to move away from us. As in the case of sound, this means that the light will have its wavelength elongated, and hence its spectrum will be shifted toward the red end of the spectrum.
In the years following his proof of the existence of other galaxies, Hubble spent his time cataloguing their distances and observing their spectra. At that time most people expected the galaxies to be moving around quite randomly, and so Hubble expected to find as many blueshifted spectra as red-shifted ones. It was quite a surprise, therefore, to find that most galaxies appeared red-shifted: nearly all were moving away from us! More surprising still was the finding that Hubble published in 1929: even the size of a galaxy’s red shift is not random but is directly proportional to the galaxy’s distance from us. In other words, the farther a galaxy is, the faster it is moving away! And that meant that the universe could not be static or unchanging in size, as everyone previously had thought. It is in fact expanding; the distance between the different galaxies is growing all the time.
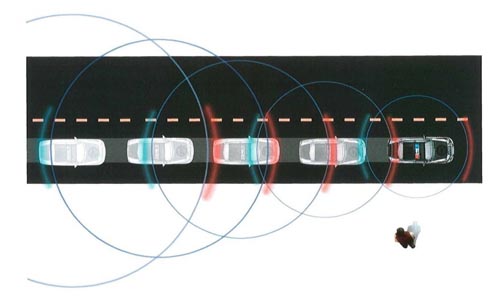
Doppler Effect
When a wave source moves toward an observer, its waves appear to have a shorter wavelength If the wave source moves away, its waves appear to have a longer wavelength. This is called the Doppler effect
The discovery that the universe is expanding was one of the great intellectual revolutions of the twentieth century. With hindsight, it is easy to wonder why no one had thought of it before. Newton, and others, should have realized that a static universe would be unstable, for there is no comparable repulsive force to balance the gravitational pull that all the stars and galaxies exert upon each other. Therefore, even if at some time the universe had been static, it wouldn’t have remained static because the mutual gravitational attraction of all the stars and galaxies would soon have started it contracting. In fact, even if the universe was expanding fairly slowly, the force of gravity would cause it eventually to stop expanding, and it would start to contract. However, if the universe was expanding faster than a certain critical rate, gravity would never be strong enough to stop it, and it w ould continue to expand forever. This is a bit like what happens when you fire a rocket upward from the surface of the earth. If the rocket has a fairly low speed, gravity will eventually stop it, and it will start falling back. On the other hand, if the rocket has more than a certain critical speed (about seven miles per second), gravity will not be strong enough to pull it back, so it will keep going away from the earth forever.