A Briefer History of Time (4 page)

It is a matter of common experience that we can describe the position of a point in space by three numbers, or coordinates. For instance, we can say that a point in a room is seven meters from one wall, three meters from another, and five meters above the floor. Or we could specify that a point is at a certain latitude and longitude and a certain height above sea level. We are free to use any three suitable coordinates, although they have only a limited range of validity. It would not be practical to specify the position of the moon in terms of miles north and miles west of Piccadilly Circus and feet above sea level. Instead, we might describe it in terms of distance from the sun, distance from the plane of the orbits of the planets, and the angle between the line joining the moon to the sun and the line joining the sun to a nearby star such as Proxima Centauri. Even these coordinates would not be of much use in describing the position of the sun in our galaxy or the position of our galaxy in the local group of galaxies. In fact, we may describe the whole universe in terms of a collection of overlapping patches. In each patch, we can use a different set of three coordinates to specify the position of a point.

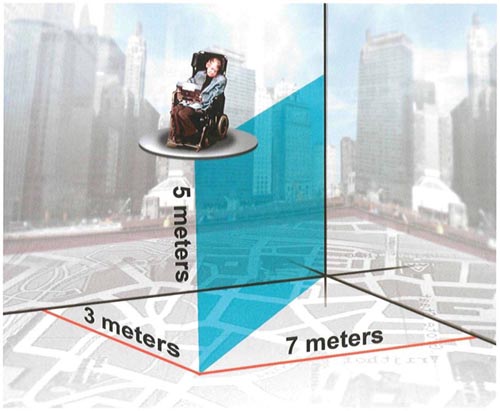
Coordinates in Space

When we say that space has three dimensions, we mean that it takes three numbers, or
coordinates,
to specify a point. If we add time to our description, then space becomes space-time, with four dimensions.

In the space-time of relativity, any event—that is, anything that happens at a particular point in space and at a particular time—can be specified by
four
numbers or coordinates. Again, the choice of coordinates is arbitrary: we can use any three well-defined spatial coordinates and any measure of time. But in relativity, there is no real distinction between the space and time coordinates, just as there is no real difference between any two space coordinates. We could choose a new set of coordinates in which, say, the first space coordinate was a combination of the old first and second space coordinates. So instead of measuring the position of a point on the earth in miles north of Piccadilly and miles west of Piccadilly, we could use miles northeast of Piccadilly and miles northwest of Piccadilly. Similarly, we could use a new time coordinate that was the old time (in seconds) plus the distance (in light-seconds) north of Piccadilly

Another well-known consequence of relativity is the equivalence of mass and energy, summed up in Einstein’s famous equation E=mc
²
(where E is energy, m is mass, and c is the speed of light). People often employ this equation to calculate how much energy would be produced if, say, a bit of matter was converted into pure electromagnetic radiation. (Because the speed of light is a large number, the answer is a lot—the weight of matter converted to energy in the bomb that destroyed the city of Hiroshima was less than one ounce.) But the equation also tells us that if the energy of an object increases, so does its mass, that is, its resistance to acceleration, or change in speed.

One form of energy is energy of motion, called kinetic energy. Just as it takes energy to get your car moving, it takes energy to increase the speed of any object. The kinetic energy of a moving object is identical to the energy you must expend in causing it to move. Therefore, the faster an object moves, the more kinetic energy it possesses. But according to the equivalence of energy and mass, kinetic energy adds to an object’s mass, so the faster an object moves, the harder it is to further increase the object’s speed.

This effect is really significant only for objects moving at speeds close to the speed of light. For example, at 10 percent of the speed of light, an object’s mass is only 0.5 percent more than normal, while at 90 percent of the speed of light it would be more than twice its normal mass. As an object approaches the speed of light, its mass rises ever more quickly, so it takes more and more energy to speed it up further. According to the theory of relativity, an object can in fact never reach the speed of light, because by then its mass would have become infinite, and by the equivalence of mass and energy, it would have taken an infinite amount of energy to get it there. This is the reason that any normal object is forever confined by relativity to move at speeds slower than the speed of light. Only light, or other waves that have no intrinsic mass, can move at the speed of light.

Einstein’s 1905 theory of relativity is called special relativity. That is because, though it was very successful in explaining that the speed of light was the same to all observers and in explaining what happens when things move at speeds close to the speed of light, it was inconsistent with the Newtonian theory of gravity. Newton’s theory says that at any given time objects are attracted to each other with a force that depends on the distance between them at that time. This means that if you moved one of the objects, the force on the other one would change instantaneously. If, say, the sun suddenly disappeared, Maxwell’s theory tells us that the earth wouldn’t get dark for about another eight minutes (since that is how long it takes light to reach us from the sun) but, according to Newtonian gravity, the earth would immediately cease to feel the sun’s attraction and fly out of orbit. The gravitational effect of the disappearance of the sun would thus have reached us with infinite speed, instead of at or below the speed of light, as the special theory of relativity required. Einstein made a number of unsuccessful attempts between 1908 and 1914 to find a theory of gravity that was consistent with special relativity. Finally, in 1915, he proposed the even more revolutionary theory we now call the general theory of relativity.

6

CURVED SPACE

EINSTEIN’S THEORY OF GENERAL RELATIVITY IS based on the revolutionary suggestion that gravity is not a force like other forces but a consequence of the fact that space-time is not flat, as had been previously assumed. In general relativity, space-time is curved, or "warped," by the distribution of mass and energy in it. Bodies such as the earth are not made to move on curved orbits bv a force called gravity; instead they move in curved orbits because they follow the nearest thing to a straight path in a curved space, which is called a geodesic. Technically speaking, a geodesic is defined as the shortest (or longest) path between two nearby points.

A geometric plane is an example of a two-dimensional flat space, on which the geodesics are lines. The surface of the earth is a two-dimensional curved space. A geodesic on the earth is called a great circle. The equator is a great circle. So is any other circle on the globe whose center coincides with the center of the earth. (The term "great circle" comes from the fact that these are the largest circles you can draw on the globe.) As the geodesic is the shortest path between two airports, this is the route an airline navigator will tell the pilot to fly along. For instance, you could fly from New York to Madrid by following your compass for 3,707 miles almost straight east, along their common line of latitude. But you can get there in 3,605 miles if you fly along a great circle, heading first northeast, then gradually turning east, and then southeast. The appearance of these two paths on a map, in which the surface of the globe has been distorted (flattened out), is deceiving. When you move "straight" east, you are not really moving straight, at least not straight in the sense of the most direct path, the geodesic.

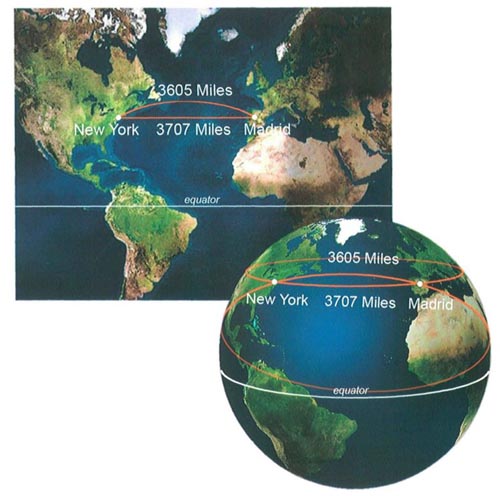
Distances on the Globe

The shortest distance between two points on the globe is along a great circle, which does not correspond to a straight line if you are looking at a flat map.

In general relativity, bodies always follow geodesics in four-dimensional space-time. In the absence of matter, these geodesics in four-dimensional space-time correspond to straight lines in threedimensional space. In the presence of matter, four-dimensional space-time is distorted, causing the paths of bodies in three-dimensional space to curve in a manner that in the old Newtonian theory was explained by the effects of gravitational attraction. This is rather like watching an airplane flying over hilly ground. The plane might be moving in a straight line through three-dimensional space, but remove the third dimension-height-and you find that its shadow follows a curved path on the hilly two-dimensional ground. Or imagine a spaceship flying in a straight line through space, passing directly over the North Pole. Project its path down onto the two-dimensional surface of the earth and you find that it follows a semicircle, tracing a line of longitude over the northern hemisphere. Though the phenomenon is harder to picture, the mass of the sun curves space-time in such a way that although the earth follows a straight path in four-dimensional space-time, it appears to us to move along a nearly circular orbit in three-dimensional space.

Path of a Spacecraft’s Shadow

Projected onto the two-dimensional globe, the path of a spacecraft flying along a straight line in space will appear curved

Actually, although they are derived differently, the orbits of the planets predicted by general relativity are almost exactly the same as those predicted by the Newtonian theory of gravity. The largest deviation is in the orbit of Mercury, which, being the planet nearest to the sun, feels the strongest gravitational effects and has a rather elongated elliptical orbit. General relativity predicts that the long axis of the ellipse should rotate about the sun at a rate of about one degree per ten thousand years. Small though this effect is, it had been noticed (see Chapter 3) long before 1915, and it served as one of the first confirmations of Einstein’s theory. In recent years, the even smaller deviations of the orbits of the other planets from the Newtonian predictions have been measured by radar and found to agree with the predictions of general relativity

Light rays too must follow geodesics in space-time. Again, the fact that space is curved means that light no longer appears to travel in straight lines in space, so general relativity predicts that gravitational fields should bend light. For example, the theory predicts that the path of light near the sun would be slightly bent inward, on account of the mass of the sun. This means that light from a distant star that happened to pass near the sun would be deflected through a small angle, causing the star to appear in a different position to an observer on the earth. Of course, if the light from the star always passed close to the sun, we would not be able to tell whether the light was being deflected or if instead the star was really where we seem to see it. However, as the earth orbits around the sun, different stars appear to pass behind the sun and have their light deflected. They therefore change their apparent position relative to the other stars.

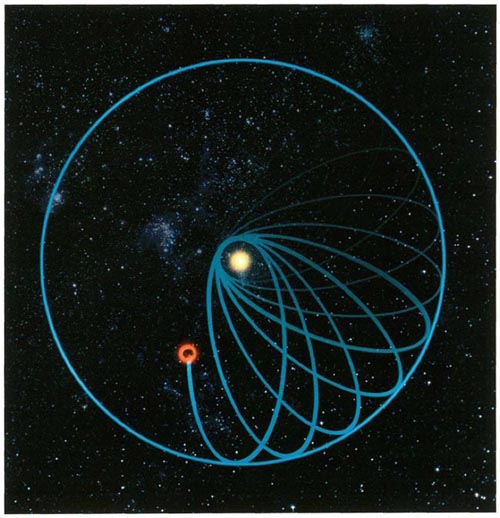
Precession of Mercury’s Orbit

As Mercury repeatedly orbits the sun, the long axis of its elliptical path slowly rotates, coming full circle roughly every 360,000 years

Bending of Light Near the Sun

When the sun lies almost directly between the earth and a distant star, its gravitational field deflects the star’s light, altering its apparent position.

It is normally very difficult to see this effect, because the light from the sun makes it impossible to observe stars that appear near to the sun in the sky. However, it is possible to do so during an eclipse of the sun, when the moon blocks the sun’s light. Einstein’s prediction of light deflection could not be tested immediately in 1915, because the First World War was in progress. It was not until 1919 that a British expedition, observing an eclipse from the coast of West Africa, showed that light was indeed deflected by the sun, just as predicted by the theory. This proof of a German theory by British scientists was hailed as a great act of reconciliation between the two countries after the war. It is ironic, therefore, that later examination of the photographs taken on that expedition showed the errors were as great as the effect they were trying to measure. Their measurement had been sheer luck, or perhaps a case of knowing the result they wanted to get-not an uncommon occurrence in science. The light deflection has, however, been accurately confirmed by a number of later observations.

Another prediction of general relativity is that time should appear to run slower near a massive body such as the earth. Einstein first realized this in 1907, five years before he realized that gravity also altered the shape of space, and eight years before he completed his theory. He derived the effect using his principle of equivalence, which played the role in general relativity that the fundamental postulate played in the special theory.

Recall that the fundamental postulate of special relativity stated that the laws of science should be the same for all freely moving observers, no matter what speed they were moving at. Roughly speaking, the principle of equivalence extends this to those observers who are not freely moving but are under the influence of a gravitational field. In a precise statement of the principle there are some technical points, such as the fact that if the gravitational field is not uniform, you must apply the principle separately to a series of small, overlapping patches, but we won’t concern ourselves with that here. For our purposes, we can state the principle this way: in small enough regions of space, it is impossible to tell if you are at rest in a gravitational field or uniformly accelerating in empty space.

Imagine that you are in an elevator in empty space. There is no gravity, no "up" and no "down." You are floating freely. Now the elevator starts to move with constant acceleration. You suddenly feel weight. That is, you feel a pull toward one end of the elevator, which suddenly seems to you to be the floor! If you now hold out an apple and let go, it drops to the floor. In fact, now that you are accelerating, everything that happens inside the elevator will unfold exactly as it would if the elevator was not moving at all but at rest in a uniform gravitational field. Einstein realized that just as you cannot tell from inside a train whether or not you are moving uniformly, you also cannot tell from inside the elevator whether you are uniformly accelerating or in a uniform gravitational field. The result was his principle of equivalence.

The principle of equivalence, and the above example of it, is true only if inertial mass (the mass in Newton’s second law that determines how much you accelerate in response to a force) and gravitational mass (the mass in Newton’s law of gravity that determines how much gravitational force you feel) are the same thing (see Chapter 4). That’s because if both kinds of mass are the same, then all objects in a gravitational field will fall at the same rate, no matter what their mass. If this equivalence weren’t true, then under the influence of gravity some objects would fall faster than others, which would mean you could distinguish the pull of gravity from uniform acceleration, in which everything does fall at the same rate. Einstein’s use of the equivalence of inertial and gravitational mass to derive his principle of equivalence, and eventually all of general relativity, amounts to a relentless march of logical reasoning unmatched in the history of human thought.

Now that we know the principle of equivalence, we can start to follow Einstein’s logic by doing another thought experiment that shows why time must be affected by gravity. Imagine a rocket ship out in space. For convenience, imagine that the rocket ship is so long that light takes one second to traverse it from top to bottom. Finally, suppose there is an observer at the ceiling of the rocket ship and another at the floor, each with identical clocks that tick once each second.

Suppose the ceiling observer w aits for the clock to tick, and then immediately sends a light signal down to the floor observer. The ceiling observer does this once more the next time the clock ticks. According to this setup, each signal travels for one second and then is received by the floor observer. So just as the ceiling observer sends two light signals a second apart, the floor observer receives two, one second apart.