125 Physics Projects for the Evil Genius (12 page)

3. Holding the tube in one hand, swing the rubber stopper in a smooth, horizontal circle.

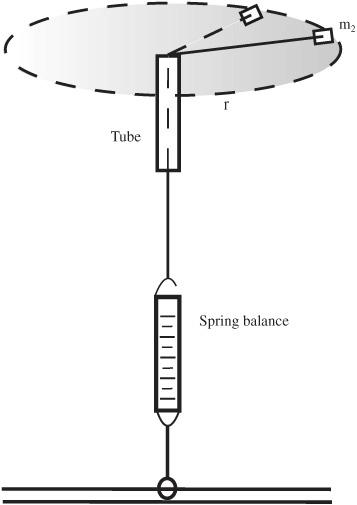
Figure 13-2
Using a spring scale to measure centripetal acceleration
.

4. Measure how many seconds it takes to make ten rotations, and then divide by ten to get the period for one rotation. Be careful to count the first rotation at the
end, rather than at the beginning
, of the rotation. It may help to count “zero” when you start, and then to count “one” when the first rotation is completed.

5. Using the marker, place a series of marks at 1 centimeter intervals, starting at the loop for the hanging mass.

6. Using the meter stick, identify the distance between the top of the tube and the rubber stopper associated with the mark closest to the hanging weight. You can now easily measure the radius by subtracting 1 centimeter for every mark below the tube that you can count. (You can also determine the radius by measuring the length of string below the tube and subtracting from the total length of the string.) You can also use a piece of tape or a paper clip to mark the position of the string to give a radius that you measure before spinning. However you do it, make sure that nothing restricts the free movement of the string through the tube.

1. Set the spring balance to zero. (It’s preferable that the spring balance reads directly in newtons. If it reads in grams, multiply by 0.0098 to convert to newtons.)
   
2. Attach the bottom of the spring balance to a clamp on the table and the other end to the string coming from the tube. See the previous
   Figure 13-2
   .
   
3. Start the rubber stopper going in a circle.
   
4. Measure the radius from the center of the circle to the rubber stopper (in meters). This should remain nearly the same for all these measurements.
   
5. Measure the period or the number of seconds it takes to go ten complete rotations.
   
6. Calculate the velocity (in meters per second) by using v = 2πr/T, where
   r
   is the radius (in meters) and
   T
   is the period (in seconds).
   
7. Measure the force on the spring scale while the washer is spinning. If you are using a mass hanging from the string, the force (in newtons) is equal to the weight of the mass (mass in
   kg
   times 9.8 or mass in
   g
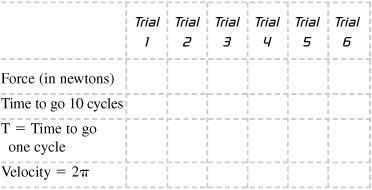
   times 0.098).
   
8. Increase or decrease the velocity while maintaining a fixed radius. For each new velocity, measure the force on the spring scale. Repeat for several velocity and force measurements at (nearly) the same radius, and then plot the results.
   

Radius for all trials = ____ meters

1. With the spring balance set to zero and attached to the table as done previously, start the rubber stopper spinning at a medium-paced period.
   
2. Measure the force and record the mass of the rubber stopper.
   
3. Tie a second stopper (to double the mass) at the end of the string.
   
4. Repeat by adding a third and then a fourth rubber stopper.
   
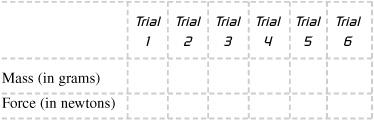
5. Complete the data table, plot your results, and describe the relationship between force and mass for fixed radius and period from your data.
   

Radius for all trials = (constant) ____ meters

Period for all trials = (constant) ____ seconds

This part is more complicated than the previous two investigations and will require a greater degree of skill and patience.

1. Zero the spring balance and clamp to the table, as done previously.
   
2. Start the rubber stopper going in a circle.
   
3. Measure the radius, measure the force on the spring scale, and then measure the period as previously described. (Throughout this part of the experiment, the velocity needs to stay as constant as possible, so the only variables being studied are force and radius. Measure the period and from that determine the velocity. As the radius gets larger, it will be necessary to allow the period to decrease to maintain a constant velocity. If the velocity is reasonably close to the first reading, record the radius and the force, as well as the spring scale. Otherwise, adjust the rate of turning and try again until the velocity is reasonably close.)
   
4. Adjust the radius (either longer or shorter) while continuing to turn at the same rate. For each new radius, measure the force on the spring scale.
   
5. Repeat for several radius and force measurements at (nearly) the same period.
   
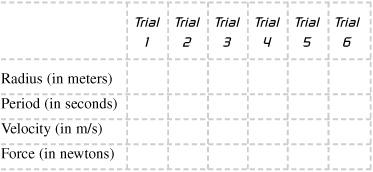
6. Complete the following data table and plot the results.
   

Period for all trials = ____ seconds

This project leads to the following conclusions:

1. The faster the rotation (or the shorter the period of rotation), the greater the centripetal force needed to maintain circular motion.

For a 12-gram rubber stopper, the expected results are shown in
Figure 13-3
. This shows the relationship is
not
linear, but that it increases more rapidly as the velocity increases.

2. The greater the mass, the greater the force needed to keep the rubber stopper going at a given speed at a particular radius. This result is expected to be linear.

3. For a given rotational speed, the shorter the string, the greater the force needed.

For a 12-gram rubber stopper, the expected results are shown in
Figure 13-4
, which shows an inverse relationship between force and string length.

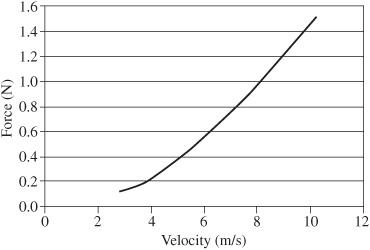
Figure 13-3
Centripetal force versus velocity
.

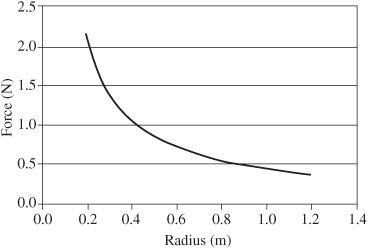
Figure 13-4
Force versus string length
.

The “string” that keeps an object going around in a circle is provided by a centripetal force. In this case, it is literally a string. In the case of a satellite or planet, the “string” is the gravitational force.

The faster the object goes (for a given radius), the greater the force, according to the equation:

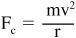
where
F
_c
is the centripetal force,
m
is the mass of the spinning object (the washer in our case),
v
is the velocity of the washer, and
r
is the radius of the circle.

Given the data shown in
Figure 13-3
, we can determine that force increases with the square of the rubber stopper’s velocity in one of two ways:

1. Use a curve-fitting program, such as Excel. From a scatter plot, with the data selected, go to the Chart menu, select Add Trendline, and then select a power fit option. Select Add Equation to the Chart from the Options tab. This displays the mathematical model for your data. The expected result is for this to be the form y = x
²
or close to it.