125 Physics Projects for the Evil Genius (15 page)
Read 125 Physics Projects for the Evil Genius Online
Authors: Jerry Silver

Physics alert
:
there is really no such thing as a centrifugal force
. The water is given a velocity and is forced into a circular path by the centripetal force exerted by the bottom of the bucket on the water. If the bucket is moving fast enough, the centripetal force of the bucket is needed to keep it going in a circle. If the bucket is not going fast enough, gravity would be great enough to cause the water to spill out.
The centripetal force on the water is provided by the bottom of the bucket. The handle of the bucket provides a centripetal force on the bucket itself. The water will not fall if the rate of rotation is high enough that the centripetal force is at least as great as gravity.
Gravity
Feather and coin
.
Does an object with a greater mass fall faster than an object with a lower mass?
This is a fundamental issue that was addressed by Galileo, as well as Apollo astronauts on the moon. After doing this experiment, you can weigh in on this question.
- feather
- coin
- clear cylindrical plastic tube
- caps to fit the end of the tube—one closed and one with a vacuum fitting
- vacuum pump
- Put the coin and the feather in the tube.
- Insert the end caps in each of the ends of the tube.
- With both objects on the bottom end cap, invert the tube and let the feather and the coin fall in the tube. Make sure both are able to fall freely without interference.
- Attach the vacuum pump to the tube and evacuate the air from inside the tube, as shown in
Figure 18-1
. - Invert the tube and observe the results again.

Figure 18-1
Clear plastic tube attached to vacuum pump
.
With air in the tube, the coin will fall faster, as shown in
Figure 18-2
.

Figure 18-2
With air present in the tube, the coin fall faster
.
With air removed from the tube, both objects fall at the same rate, as shown in
Figure 18-3
.
(Two things could result in an unintended outcome, which should be avoided if possible: With air in the tube, the coin might push the feather toward the bottom at a faster rate than it would fall on its own. Also, some electrostatic drag might develop between the feather and the plastic, which slows the descent of the feather in a vacuum.)

Figure 18-3
With air removed from the tube, both objects fall at the same speed
.
There is no doubt that the gravity of the Earth exerts a greater force on a more massive object. However, the more massive object requires precisely that same amount of larger force to cause it to accelerate. The upshot is that all objects on the surface of the Earth accelerate at the same constant rate.
This experiment has a number of variations, including:
- Compare the descent of a crumpled sheet of paper with an unfolded sheet of paper (both of the same mass).
- Compare the descent of a single pencil with several pencils bundled together.
- Tie a weight (such as a large stainless steel nut) to a string at the following intervals: 125 cm, 80 cm, 45 cm, 20 cm, 5 cm. Hold the string vertically. When dropped, each weight hits the floor in the same time interval. This is because the distance each weight falls is proportional to the
square
of the time that it is falling. These intervals are built into the spacing of the weights, so they should hit at the same time interval. - Which falls faster (in air): a book or a dollar bill? Certainly, if they’re dropped side by side, the book will fall fastest. However, if the dollar bill is placed on top of the book or below the book, the effect of air resistance will be eliminated and they will fall together.
Gravitational acceleration (in a vacuum) is a constant. Specifically, it does not depend on the mass of the falling object.
How fast do things fall
?
Objects exposed to the force of gravity accelerate at the same rate. We proved that in the previous experiment. Here, we measure the rate of gravitational acceleration for all objects on the earth.
You measure acceleration two different ways in this experiment. In the first method, you use a stopwatch. We call this a
ballpark experiment
, which means we expect it to give a rough approximation rather than a very accurate result.
The second method involves the use of a motion sensor, which offers a greater degree of precision.
- various objects: baseballs, golf balls, bowling balls, your physics textbook
- stopwatch
- tape measure
- motion sensor with DataStudio software
- ring stand or other support to orient the motion sensor vertically, looking downward
- basketball, softball
- Use the tape measure to identify the distance the object will be dropped.
- One person drops the object and the other person times the trip down.
- Start the timer just as the object is released and stop it at the precise time it hits the ground. Try to avoid anticipating the release that will give too large a time measurement and an understated value for gravitational acceleration.
- Calculate the gravitational acceleration using the equation g = 2d/t
2
, where
d
is the distance in meters and
t
is the time in seconds. Gravitational acceleration is measured in m/s
2
, which is read as meters per second squared or meters per second per second.
1. Set up a motion detector mounted on a table with an unobstructed view of the floor, as shown in
Figure 19-1
.
2. Set up the motion detector to read distance versus time and velocity versus time. This can be accomplished by selecting the “velocity” file that comes with the DataStudio software package.

Figure 19-1
Motion sensor aligned to measure vertical motion. Courtesy PASCO
.
3. This measurement works best by increasing the frequency of the motion sensor measurement by increasing the sampling from 10 per second to 50 per second.
4. Align the motion sensor in the vertical direction.
5. Hold the ball just under the motion sensor, as shown in
Figure 19-2
. Start the readings and release the ball. Try to avoid imparting any vertical momentum to the ball by letting it drop without an initial push or delayed release.
6. Capture the motion of the ball through several bounces.
7. Measure the slope of the velocity versus time graph. Use either the initial descent or the first bounce. The initial descent has the advantage of having the largest statistical sample. The first bounce has the advantage of being free of errors associated with the release.
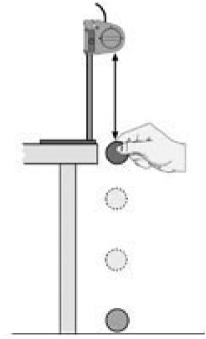
Figure 19-2
Courtesy PASCO
.
For either method, the accepted value for gravitational acceleration is about 9.81 m/s
2
. This may vary slightly with location and elevation.
For a typical outdoor high-school athletic bleacher about 15 feet above the ground (about 4.6 meters), an object will take about 1 second to fall. We learn in the next project that a person’s reaction time can easily be as much as ¼ second. As a result, any given measurement may have an error of as much as about 25 percent. (This can be even greater because there can be non-offsetting errors for the start and stop time of the measurement.) This is not very precise, but it puts us in the ballpark. It is hard to improve on this because of the limitation in measuring time inherent in the use of a stopwatch. Some people find that listening for the ball to hit the ground is easier to time than trying to observe it visually. A greater distance to fall also reduces errors
because the reaction time is a smaller percentage of the overall time measured.
The following chart summarizes expected times for various distances. Times measured in this range gives reasonable values for gravitational acceleration,
g
.