125 Physics Projects for the Evil Genius (11 page)
Read 125 Physics Projects for the Evil Genius Online
Authors: Jerry Silver

Figure 11-2
The “coconut” is shot by a PASCO launcher with an aluminum-foil switch taped in front
.
- laser pointer
- various types of the monkey and coconut apparatus are also available commercially
- Set up the apparatus, as shown in
Figure 11-3
. - Apply the DC voltage to the electromagnet circuit.
- Arm the launcher (by pushing the ball in with the plunger in the case of the PASCO launcher).
- Close the switch.
- Aim the launcher directly at the target, either visually or aided by the laser pointer.
- Shoot the projectile. As the projectile emerges from the launcher, it causes the switch to open and deactivates the electromagnet. This releases the metal lid (monkey) as the projectile is shot at it.
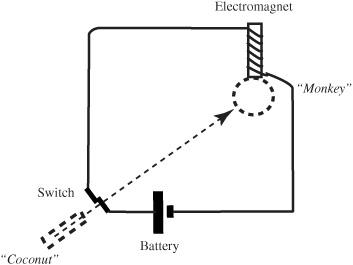
Figure 11-3
Electrical connections for the monkey-and-coconut apparatus
.
The answer to the question posed previously is: b) firing at the monkey. As long as the monkey is in range, firing directly at the monkey will cause a direct hit every time.
Both the monkey and the coconut are subjected to the same gravitational acceleration. If the coconut is aimed directly at the monkey in the tree, the coconut will fall from that straight line path and follow the curved (parabolic) path that projectiles normally take. See
Figure 11-4
. As a result, the coconut falls away from that straight-line path at precisely the same rate as the monkey falls downward. This causes the monkey and the coconut to be in the same place before the monkey hits the ground.
Suppose our monkey gets tired of having coconuts thrown at him. Where should he aim a coconut of his own that he throws to deflect the one that is thrown at him? This can be set up using two projectile launchers, but it requires much more precision because the balls have a small diameter. The answer is the same as the previous one. The monkey should aim directly at the hunter.
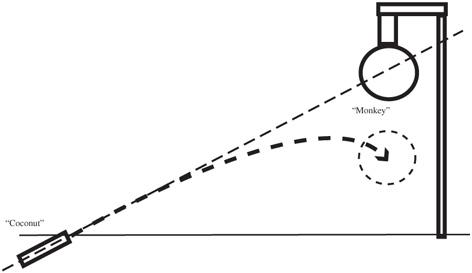
Figure 11-4
You aim directly at the monkey. He will fall as fast as the coconut and will catch it on the way down
.
This project illustrates one of the underlying concepts of projectiles, which is the idea that the horizontal and vertical components of motion are completely independent and do not influence each other. The monkey does not have horizontal motion, but the coconut does. They both have vertical motion, which experiences the same rate of acceleration, regardless of the horizontal motion.
Going Around in Circles
What is the direction of a satellite’s velocity
?
What is the direction of an object moving in a circle? A common misconception is that the velocity, at any given time, is pointed in a circle. This simple experiment illustrates that the direction of an object moving in a circular path is in a straight line, as shown in
Figure 12-1
.
- 1 marble
- roll of masking tape
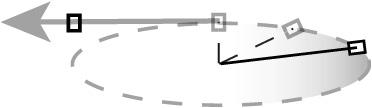
Figure 12-1
The velocity of an object in circular motion at any given time is a straight line tangent to the circle
.
Marble and tape ring
- Place the marble in the center of a tape roll.
- Get the marble spinning rapidly in a circular path, as shown in
Figure 12-2
. - Quickly lift the masking tape roll and observe the path the marble takes when it’s no longer constrained by the tape, as
Figure 12-3
shows.
The marbles travel in a straight path as soon as they are released from the roll of tape.

Figure 12-2
Marble kept in a circular path by centripetal force from a tape roll
.
Circular motion
is the result of a centripetal force that changes the direction of motion from a straight line path to a circular path. The centripetal force is provided by the string in the case of the ball, by the interior wall of the masking tape in the case of the rotating marble, and by gravity in the case of satellites and planets. Objects traveling in a circle at any given time have an instantaneous velocity that heads in a perfectly straight line. This is actually a consequence of Newton’s first law of motion, which we explore later: an object in motion tends to stay in motion in a straight line, unless it’s acted upon by an external force.

Figure 12-3
Free marble moving along a straight path
.
Attach a string to a ball and spin the ball in a circle. Cut the string or let the string go and observe the path of the ball after it is released. Without the centripetal force provided by the string, the ball moves in a straight line.
An object moving in a circle has a velocity that takes it in a straight line at any given point in time. A centripetal force that continuously changes the direction is needed to form the circular path.
Centripetal force. What is the string that keeps the planets in orbit
?
In this experiment, you investigate how objects move in a circle. Gravitational force keeps the planets and satellites in their orbits. The same physical laws determine how a rubber stopper on a string moves in a circle.
- 1.5 meter of light, strong string
- 1 rubber stopper (1 or 2 holes)
- glass, plastic, or smooth cardboard tube—about 5 inches in length with a small diameter, but large enough for the string to move through freely
- spring scale—10 N
- clamp to attach the spring balance to the table
- hooked masses: 10, 20, 50, 100 g
- meterstick
- marker pen
- safety goggles—(you will be swirling an object in a circle, so safety goggles should be worn to prevent the possibility of eye injury)
Set up the apparatus as shown in
Figure 13-1
.
- Tie the string securely to the rubber stopper.
- Feed the string through the glass or cardboard tube.
- With about 1 meter of string length between the tube and the rubber stopper, cut the string, so about 25 centimeters of string is below the tube.
Each of these experiments uses the same basic technique. Getting the hang of it may take a little practice.
1. Put on your safety glasses. (The spinning washer poses a potential eye hazard.)
2. You have two ways to measure the centripetal force required to keep the washer moving in a circle under a given set of conditions.

Figure 13-1
Apparatus for exploring centripetal force. Courtesy PASCO
.
– One way is to hang a known weight from the string,
Figure 13-1
shows this approach. The force is the weight (in newtons) which is determined by multiplying the mass (in kg) by gravitational acceleration (9.8 m/s
2
). This technique is simple enough, but it requires a certain degree of skill to keep the radius fixed for a given measurement.
– The other approach is to measure the force directly using a spring scale, as indicated in
Figure 13-2
. In this case, you need to coordinate your movements, so the force stays nearly constant for a given measurement. (Note: Holding the string at an angle slightly off vertical can introduce just enough friction to stabilize the reading while introducing an error of only a few percent.)