Why Beauty is Truth (54 page)
Read Why Beauty is Truth Online
Authors: Ian Stewart


Quantum theory explains all physical forces in terms of exchanges of particles. Just as the tennis ball holds the two players together at opposite ends of the court as long as the game continues, so various particles carry the electromagnetic, strong, and weak forces. The electromagnetic force is carried by photons. The strong force is carried by gluons, the weak force by intermediate vector bosons, otherwise known as “weakons.” (Don't blame meâI didn't invent these names, which are mostly historical accidents.) Finally, it is widely conjectured that gravity must be carried by a hypothetical particle called the
graviton.
No one has yet observed a graviton.
The large-scale effect of all these carrier particles is to fill the universe with “fields.” Gravitational interactions create a gravitational field, electromagnetic ones create an electromagnetic field, and the two nuclear forces
together create something called a YangâMills field, after the physicists Chen Ning Yang and Robert Mills.
We can summarize the main characteristics of the fundamental forces in a kind of physicist's shopping list:
Â
â¢Â
Gravity:
Strength 6 Ã 10
â39
, range infinite, carried by gravitons (not observed, should have mass 0, spin 2), forms the gravitational field.
â¢Â
Electromagnetism:
Strength 10
â2
, range infinite, carried by photons (mass 0, spin 1), forms the electromagnetic field.
â¢Â
Strong force:
Strength 1, range 10
â15
meters, carried by gluons (mass 0, spin 1), forms one component of the YangâMills field.
â¢Â
Weak force:
Strength 10
â6
, range 10
â18
meters, carried by weakons (large mass, spin 1), forms the other component of the YangâMills field.
Â
You may feel that 36 fundamental particles, plus assorted gluons, is not a big improvement on sixty or more, but quarks form a highly structured family with a huge amount of symmetry. They are all variations on the same themeâunlike the wild zoo of particles that physicists had to deal with before quarks were discovered.
The description of fundamental particles in terms of quarks and gluons is known as the standard model. It fits experimental data extremely well. Some of the masses of some of the particles have to be adjusted to fit observations, but once you've done that, all the other masses slot neatly into place. The logic is not circular.
Quarks are bound together very tightly, and you never see an isolated quark. All you can observe are the combinations of twos and threes. Nevertheless, particle physicists have confirmed the existence of quarks indirectly. They're not just a clever numerological variation on the zoo. And to those who believe that the universe is at heart beautiful, the symmetry properties of quarks clinch it.

According to quantum chromodynamics, a proton is made from three quarksâtwo up, one down. If you took the quarks out of a proton, shuffled them, and put them back, you would still have a proton. So the laws for protons ought to be symmetric under permutations of their constituent
quarks. More interestingly, the laws also turn out to be symmetric under changes to the
type
of quark. You could turn an up quark into a down one, say, and the laws would still work.
This implies that the actual symmetry group here is not just the group of six permutations of three quarks, but a closely related
continuous
group, SU(3), one of the simple groups on Killing's list. Transformations in SU(3) leave the equations for laws of nature unchanged, but they can change the
solutions
to those equations. Using SU(3) you can “rotate” a proton into a neutron, for instance. All you have to do is turn all of its quarks upside down, so that two up and one down become two down and one up. The world of fermions has SU(3) symmetry, and the symmetries act by changing one fermion into another.
Two further symmetry groups contribute to the standard model. The gauge symmetries of the weak force, SU(2), can change an electron into a neutrino. SU(2) is another group on Killing's list. And our old friend the electromagnetic field has U(1) symmetryânot the Lorentz symmetries of Maxwell's equations, but the gauge (i.e., local) symmetry of phase changes. This group just misses Killing's list because it is not SU(1), but it is morally on the list, since it's a very close relative.
The electroweak theory unified electromagnetism and the weak force by combining their gauge groups. The standard model incorporates the strong force as well, providing a single theory for all fundamental particles. It does this in a very direct manner: it just lumps all three gauge groups together as SU(3) Ã SU(2) Ã U(1). This construction is simple and straightforward but not terribly elegant, and it makes the standard model resemble something built out of chewing gum and string.
Suppose you own a golf ball, a button, and a toothpick. The golf ball has spherical symmetry SO(3), the button has circular symmetry SO(2), and the toothpick has (say) just a single reflectional symmetry O(1). Can you find some unified object that has all three types of symmetry? Yes, you can: put all three into a paper bag. Now you can apply SO(3) to the contents of the bag by rotating the golf ball, SO(2) by rotating the button, and O(1) by flipping the toothpick. The symmetry group of the bag's contents is SO(3) Ã SO(2) Ã O(1). This is how the standard model combines symmetries, but instead of using rotations it uses the “unitary transformations” of quantum mechanics. And it suffers from the same defect: it just lumps three systems together and combines their symmetries in an obvious, and rather trivial, way.
A much more interesting way to combine the three symmetry groups would be to build something that contained the same objects but was more elegant than a paper bag. Maybe you could balance the toothpick on the golf ball and stick a button on the end of it. You could even have a whole system of toothpicks, like the spokes of a wheel; put the button at the hub, spin the wheel on top of the golf ball. If you were really clever, maybe the combined object would have lots and lots of symmetry, say the group K(9). (There is no such group. I made it up for the sake of this discussion.) The separate symmetry groups SO(3), SO(2), and O(1) might with luck be subgroups of K(9). That would be a far more impressive way to unify the golf ball, button, and toothpick.
Physicists felt the same way about the standard model, and they wanted K(9) to be something on Killing's list or very close to it, because Killing's groups are the fundamental building blocks of symmetry. So they invented a whole series of Grand Unified Theories, or GUTs, based on groups like SU(5), O(10), and Killing's mysterious exceptional group E
6
.
The GUTs seemed to suffer from the same defect as KaluzaâKlein theoryâa lack of testable predictions. But then a really interesting prediction appeared. It was certainly new, so new that it seemed unlikely to be true, but it was testable. All GUTs predict that the proton can be “rotated” into an electron or a neutrino. So protons are
unstable
, and in the long run all matter in the universe should decay into radiation. The calculations said that on average, the life of a proton should be around 1029 years, much longer than the age of the universe. But individual protons would sometimes decay much sooner, and if you had enough protons, you might spot one decaying.
A big tank of water has more than enough protons for a few to decay each year. By the end of the 1980s there were six experiments running, all trying to spot a decaying proton. The biggest tank contained over 3000 tons of extremely pure water. No one saw a proton decay. Not one. Which meant that the average lifetime is at least 10
32
years. Protons live at least a thousand times longer than GUTs predict. GUTs just don't hack it. In retrospect, it would have been a bit embarrassing if proton decay had been detected, because something very important is missing from GUTs: gravity.

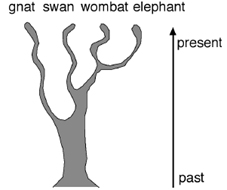
Any Theory of Everything has to explain why there are four fundamental forces, and why they take the strange forms that they do. This is a bit like
trying to find a family resemblance between an elephant, a wombat, a swan, and a gnat.
It would be much easier to organize the four forces if they could all be shown to be different aspects of a single force. In biology, this has been achieved: elephants, wombats, swans, and gnats are all members of the Tree of Life, united by their DNA, distinguished by a lengthy series of historical changes to DNA. All four evolved, step by step, from a common ancestor, which lived a billion or two billion years ago.
The common ancestor of elephants and wombats is more recent than that of, say, elephants and swans. So this divergence constitutes the most recent branching of the tree of these four species. Before that, the common ancestor of elephants and wombats split off from some ancestor of the swan. Earlier still, the common ancestor of these three species split from that of the gnat.
Speciation can be viewed as a kind of symmetry-breaking. A single species is (approximately) symmetric under any permutation of its organisms; every wombat resembles every other wombat. When there are two distinct speciesâwombats and elephantsâyou can permute the wombats among themselves, and permute the elephants, but you can't change an elephant into a wombat without someone noticing.
The physicists' explanation of the underlying unity of the four forces is similar. The role of DNA, however, is played by the
temperature
of the universeâthat is, its energy level. Although the underlying laws of nature are the same at all times, they lead to different behavior at different energiesâjust as the same laws cause water to be solid at low temperatures, liquid at medium ones, and a gas at high ones. At very high temperatures, the water molecules break up to form a
plasma
, composed of separate particles
.
At higher temperatures still, the particles themselves break to form a quarkâgluon plasma.