Why Beauty is Truth (25 page)
Read Why Beauty is Truth Online
Authors: Ian Stewart

The police report on the duel suggests that the other participant was one of Galois's revolutionary comrades, and the duel was exactly what it
appeared to be. This theory is largely borne out by Galois's own words on the matter: “I beg patriots and my friends not to reproach me for dying otherwise than for my country. I die the victim of an infamous coquette. It is in a miserable brawl that my life is extinguished. Oh! why die for so trivial a thing, for something so despicable! . . . Pardon for those who have killed me, they are of good faith.” Either he was unaware that he was the victim of a political plot, or there was no plot.
It does appear that Stéphanie was at least a proximate cause of the duel. Before departing for the engagement, Galois left some final doodles on his table. They include the words “Une femme,” with the second word scribbled out. But the ultimate cause is as opaque as much else in this tale.
The mathematical story is much clearer. On 29 May, the eve of the duel, Galois wrote to Auguste Chevalier, outlining his discoveries. Chevalier eventually published the letter in the
Revue Encyclopédique.
It sketches the connection between groups and polynomial equations, stating a necessary and sufficient condition for an equation to be solvable by radicals.
Galois also mentioned his ideas about elliptic functions and the integration of algebraic functions, and other things too cryptic to be identifiable. The scrawled comment “I have no time” in the margins has given rise to another myth: that Galois spent the night before the duel frantically writing out his mathematical discoveries. But that phrase has next to it “(Author's note),” which hardly fits such a picture; moreover, the letter was an explanatory accompaniment to Galois's rejected third manuscript, complete with a marginal note added by Poisson.
The duel was with pistols. The postmortem report states that they were fired at 25 paces, but the truth may have been even nastier. An article from the 4 June 1832 issue of
Le Precursor
reported:
Paris, 1 June
âA deplorable duel yesterday has deprived the exact sciences of a young man who gave the highest expectations, but whose celebrated precocity was lately overshadowed by his political activities. The young Ãvariste Galois . . . was fighting with one of his old friends, a young man like himself, like himself a member of the Society of Friends of the People, and who was known to have figured equally in a political trial. It is said that love was the cause of the combat. The pistol was the chosen weapon of the adversaries, but because of their old friendship they could not bear to look at one another and left the decision to blind fate. At point-blank range they
were each armed with a pistol and fired. Only one pistol was charged. Galois was pierced through and through by a ball from his opponent; he was taken to the Hospital Cochin where he died in about two hours. His age was 22. L.D., his adversary, is a bit younger.
Could “L.D.” refer to Pescheux d'Herbinville? Perhaps. The letter D is acceptable because of the variable spelling of the period; the L may have been a mistake. The article is unreliable on details: it gets the date of the duel wrong, and also the day Galois died and his age. So the initial might also be wrong.
The cosmologist and writer Tony Rothman has a more convincing theory. The person who best fits the description here is not d'Herbinville but Duchâtelet, who was arrested with Galois on the Pont-Neuf. Galois's biographers Robert Bourgne and Jean-Pierre Azra give Duchâtelet's Christian name as “Ernest,” but that might be wrong, or again the L may be wrong. To quote Rothman, “We arrive at a very consistent and believable picture of two old friends falling in love with the same girl and deciding the outcome by a gruesome version of Russian roulette.”
This theory is also consistent with a final horrific twist to the tale. Galois was hit in the stomach, a wound that was almost always fatal. If the duel was at point-blank range, this is no great surprise; if at 25 paces, it is the final example of his cursed luck.
He did not die two hours later, as
Le Precursor
says, but in the Hospital Cochin the next day, on 31 May. The cause of death was peritonitis, and he refused the office of a priest. On 2 June 1832 Galois was buried in the common ditch at the cemetery of Montparnasse.
His letter to Chevalier ended with these words: “Ask Jacobi or Gauss publicly to give their opinion, not as to the truth, but as to the importance of these theorems. Later there will be, I hope, some people who will find it to their advantage to decipher all this mess.”

But what did Galois actually accomplish? What was the “mess” referred to in his final letter?
The answer is central to our tale, and not easily stated in a few sentences. Galois introduced a new point of view into mathematics, he changed its content, and he took a necessary but unfamiliar step into abstraction. In Galois's hands, mathematics ceased to be the study of numbers
and shapesâarithmetic, geometry, and ideas that developed out of them like algebra and trigonometry. It became the study of
structure.
What had been a study of
things
became a study of
processes.
We should not give Galois all the credit for this transformation. He was riding a wave that had been set in motion by Lagrange, Cauchy, Ruffini, and Abel. But he rode it with such skill that he made it his own; he was the first person seriously to appreciate that mathematical questions could sometimes be best understood by transporting them into a more abstract realm of thought.
It took a while for the beauty and value of Galois's results to percolate into the general mathematical consciousness. In fact they were very nearly lost. They were rescued by Joseph-Louis Liouville, the son of a captain in Napoleon's army who became a professor at the Collège de France. Liouville spoke to the French Academyâthe body that had mislaid or rejected Galois's three memoirsâin the summer of 1843. “I hope to interest the Academy,” he began, “in announcing that among the papers of Ãvariste Galois I have found a solution, as precise as it is profound, of this beautiful problem: whether or not there exists a solution by radicals . . .”
If Liouville had not bothered to wade through the luckless revolutionary's often untidy and confusing manuscripts, and had not devoted considerable time and effort to puzzling out what the author intended, the manuscripts might well have been thrown out with the rubbish, and group theory would have had to await some later rediscovery of the same ideas. So mathematics owes Liouville an enormous debt.
As understanding of Galois's methods grew, a new and powerful mathematical concept came into being: that of a group. An entire branch of mathematics, a calculus of symmetry called group theory, came into being and has since invaded every corner of mathematics.

Galois worked with groups of permutationsâways to rearrange a list of objects. In his case, the objects were the roots of an algebraic equation. The simplest interesting example is a general cubic equation, with three roots
a, b
, and
c.
Recall that there are six ways to permute these symbols, and thatâfollowing Lagrange and Ruffiniâwe can
multiply
any two permutations by performing them in turn. We saw, for example, that
cba
Ã
bca
=
acb.
Proceeding in this way, we can build up a “multiplication table” for all six permutations. It's easier to see what's going on if we assign
names to each permutation, say by letting
I
=
abc, R
=
acb, Q
=
bac, V
=
bca, U
=
cab
, and
P
=
cba.
Then the multiplication table looks like this:
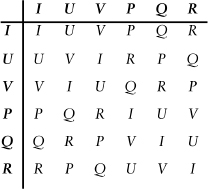
Multiplication table for the six permutations of the roots of a cubic equation.
Here the entry in row
X
and column
Y
is the product
XY
, which means “do
Y
, then do
X.
”
Galois realized that a very simple and obvious feature of this table is crucially important. The product of any two permutations is itself a permutationâthe only symbols appearing in the table are
I, U, V, P, Q, R.
Some smaller collections of permutations have the same “group property”: the product of any two permutations in the collection is also in the collection. Galois called such a collection of permutations a
group.
For example, the collection [
I, U, V
] gives a smaller table:
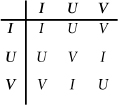
Multiplication table for a subgroup of three permutations.
and only those three symbols appear. When, as here, one group is part of another, we call it a
subgroup.
Other subgroups, namely [
I, P
], [
I, Q
], and [
I, R
], contain only two permutations. There is also the subgroup [
I
] that contains only
I.
It can be proved that the six subgroups just listed are the
only
subgroups of the group of all permutations on three symbols.
Now, said Galois (though not in this language), if we choose some cubic equation, we can look at its symmetriesâthose permutations that preserve all algebraic relations between the roots. Suppose, for example, that
a
+
b
2
= 5, an algebraic relation between the roots
a
and
b.
Is the permutation
R
a symmetry? Well, if we check the definition above,
R
keeps
a
as it was and swaps
b
with
c
, so the condition
a
+
c
2
= 5 must also hold. If it doesn't,
R
is definitely not a symmetry. If it does, you check any other valid algebraic relations among the roots, and if
R
passes
all
these tests, it is a symmetry.