Why Beauty is Truth (51 page)
Read Why Beauty is Truth Online
Authors: Ian Stewart

Einstein agonized over Kaluza's paper, because there was absolutely no reason to imagine that space-time has an extra dimension. But eventually he decided that however strange the idea might seem, it was so beautiful, and potentially so far-reaching, that it should be published. After dithering for two years, Einstein accepted Kaluza's paper for a major physics journal. Its title was “On the unity of problems of physics.”

All this talk of extra dimensions probably sounds rather vague and mystical. It is a concept associated with Victorian spiritualists, who invoked the fourth dimension as a convenient place to hide everything that didn't make sense in the familiar three. Where do spirits live? In the fourth dimension. Where does ectoplasm come from? The fourth dimension. Theologians
even placed God and His angels there until they realized that the fifth was better and the sixth better still, and that finally only an infinite dimension would really do for an omniscient and omnipresent entity.
All great fun, but not terribly scientific. So it is worth digressing to clarify the underlying mathematics. The main point is that the “dimension” of some mathematical or physical setup is the number of distinct variables needed to describe it.
Scientists spend a lot of time thinking about variablesâquantities that are subject to change. Experimental scientists spend even more time measuring them. “Dimension,” which is just a geometric way to refer to a variable, has turned out to be so useful that it is now built into science and mathematics as a standard way of thinking and is considered to be entirely prosaic and unremarkable.
Time is a nonspatial variable, so it provides a
possible
fourth dimension, but the same goes for temperature, wind speed, or the lifespan of termites in Tanzania. The position of a point in three-dimensional space depends on three variablesâits distances east, north, and upward relative to some reference point, using negative numbers for the opposite directions. By analogy, anything that depends on four variables lives in a four-dimensional “space,” and anything that depends on 101 variables lives in a 101-dimensional space.
Any complex system is inherently multidimensional. The weather conditions in your backyard depend on temperature, humidity, three components of wind velocity, barometric pressure, intensity of rainfallâthat's seven dimensions already, and there are plenty of others we might include. I bet you didn't realize you had a seven-dimensional backyard. The state of the nine (well, eight; alas, poor Pluto!) planets in the solar system is determined by six variables for each planetâthree positional coordinates and three components of velocity. So our solar system is a 54- (I mean 48)-dimensional mathematical object; and many more if you include satellites and asteroids. An economy with a million different commodities, each having its own price, lives in a million-dimensional space. Electromagnetism, which requires only six extra numbers to characterize the local states of the electric and magnetic fields, is child's play by comparison. Examples like these abound. As science became interested in systems with large numbers of variables, it was forced to come to grips with extravagantly multidimensional spaces.
The formal mathematics of multidimensional spaces is purely algebraic, based on “obvious” generalizations from low-dimensional spaces. For example, every point in the plane (a two-dimensional space) can be specified by two coordinates, and every point in three-dimensional space can be specified by three coordinates. It is a short step to define a point in four-dimensional space as a list of four coordinates, and more generally to define a point in
n
-dimensional space as a list of
n
coordinates. Then
n-
dimensional space itself (or
n
-space for short) is just the set of all such points.
Similar algebraic machinations let you work out the distance between any two points in
n
-space, the angle between any two lines, and so on. From there on out, it's a matter of imagination: most sensible geometric shapes in two or three dimensions have straightforward analogues in
n
dimensions, and the way to find them is to describe the familiar shapes using the algebra of coordinates and then extend that description to
n
coordinates.

To get a feel for
n
-space, we must somehow equip ourselves with
n-
dimensional spectacles. We can borrow a trick from the English clergyman and schoolmaster Edwin Abbott Abbott, who in 1884 wrote a short book called
Flatland.
It is about the adventures of A. Square, who lived in the two-dimensional space of a Euclidean plane. Abbott does not tell us what the initial “A” stands for: I am convinced it should be “Albert,” for reasons explained in my sequel
Flatterland
, and I will make that assumption here. Albert Square, a sensible sort, did not believe in the absurd notion of the third dimension until, one fateful day, a sphere passed through his planar universe and flung him into realms he could never have imagined.
Flatland
was a satirical look at Victorian society embedded in a parable about the fourth dimension based on a transdimensional analogy. It's the analogy, not the satire, that concerns us here. Having successfully imagined yourself as a two-dimensional creature living in a plane, blissfully unaware of the greater reality of 3-space, it is not so hard to imagine yourself as a three-dimensional creature living in 3-space, blissfully unaware of the greater reality of 4-space. Suppose Albert Square, sitting happily in Flatland, wants to “visualize” a solid sphere. Abbott achieves this by making such a sphere pass through the plane of Flatland, moving perpendicular
to it so that Albert sees its cross-sections. First he sees a point, which grows to a circular disk. The disk expands until he is seeing the equator of the sphere, after which it shrinks again to a point and then vanishes.
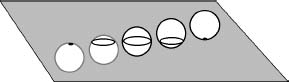
The sphere encounters Flatland.
Actually, Albert sees these disks edge-on, as line segments with graded shading, but his visual sense interprets this image as a disk, just as our stereo vision interprets a flat image as being solid.
By analogy, we can “see” a “hypersphere,” the four-dimensional analogue of a solid sphere, as a point that grows to form a sphere, expands until we see the “equator,” and then shrinks back to a point before disappearing.
Could space
really
have more than three dimensions? Not fancy mathematical fictions corresponding to nonspatial variables, but
real physical space?
After all, how can you fit the fourth dimension in? Everything's filled up already.
If you think that, you didn't listen to Albert Square, who would have argued exactly the same way about the plane. Ignoring our parochial prejudices, it seems that in principle, space might have been 4-dimensional, or million-dimensional, or whatever. Everyday observation, however, informs us that in our particular universe the good Lord settled on three dimensions for space, plus one for time.
Or did He? Whatever physics teaches us, one lesson is to be wary of everyday observation. A chair feels solid, but it's mostly empty space. Space looks flat, but according to relativity it's curved. Quantum physicists think that on very small scales space is a kind of quantum foam, mostly holes. And devotees of the “many worlds” interpretation of quantum uncertainty believe our universe is one of an infinite variety of coexisting universes, and that we occupy just a wafer-thin slice of a vast multiverse. If common sense can mislead us about those things, maybe it's wrong about the dimensionality of space or time.

The hypersphere encounters Spaceland.
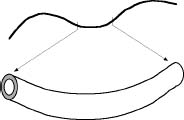
From a distance (above), a hosepipe looks one-dimensional. From close up (below) it has two additional dimensions.

Kaluza had a simple explanation for the extra dimension his theory assigned to space-time. The traditional dimensions point along straight lines, long enough to observe, billions of light years long, in fact. The new dimension, Kaluza suggested, is very different: it curls up tightly into a circle much smaller than an atom. The ripples that constitute light waves can move round the circle, because they, too, are much smaller than atoms, but matter cannot move in that direction because there isn't enough room.