Why Beauty is Truth (58 page)

In the latest version of superstrings, the biggest problem is an embarrassment of riches. Instead of making no predictions, the theory makes too
many. The “vacuum energy”—the energy content of empty space—can be almost anything, depending on how the strings wrap around inside the extra dimensions of space. The number of ways for this to happen is gigantic—around 10
⁵⁰⁰
. Different choices yield different values for the vacuum energy.

As it happens, the observed value is very, very small, around 10
^–120
, but it is not zero.

According to the conventional “fine-tuning” story, this particular value is exactly right for life to exist. Anything larger than 10
^–118
makes local space-time explode; anything smaller than 10
^–120
and space-time contracts in a cosmic crunch and disappears. So the “window of opportunity” for life is very small. By a miracle, our universe sits neatly within it.

The “weak anthropic principle” points out that if our universe were not constituted the way it is, we wouldn't be here to notice, but that leaves open the question why there is a “here” for us to occupy. The “strong anthropic principle” says that we're here because the universe was designed specially for life to exist—which is mystical nonsense. No one actually knows what the possibilities would be if the vacuum energy were markedly different from what it is. We know a few things that would go wrong—but we have no idea what might go right instead. Most of the fine-tuning arguments are bogus.

In 2000, Raphael Bousso and Joseph Polchinski proposed a different answer, using string theory and taking advantage of those 10
⁵⁰⁰
possible values for the vacuum energy. Although 10
^–120
is very small, the possible vacuum energy levels are spaced about 10
^–500
units apart, which is even smaller. So plenty of string theories give vacuum energies in the “right” range. The probability that a randomly chosen one will do that is still negligible, but Bousso and Polchinski pointed out that this is irrelevant. Eventually, the “right” vacuum energy will inevitably occur. The idea is that the universe explores all possible string theories, sticking with any given one until it causes that universe to come to bits, and then “tunneling” quantum-mechanically to some other string theory. If you wait long enough, then at some stage the universe acquires a vacuum energy that happens to be in the range suitable for life.

In 2006, Paul Steinhardt and Neil Turok proposed a variation on the “tunneling” theory: a cyclic universe that expands in a Big Bang and contracts in a Big Crunch, repeating this behavior every trillion years or so. In their model, the vacuum energy decreases in each successive
cycle, so that eventually the universe has a very small, but nonzero, vacuum energy.

In either model, a universe whose vacuum energy is low enough will hang around for a very long time. Conditions are suitable for life to arise, and life has plenty of time to evolve intelligence, and to wonder why it's there.

A
gaggle of geese, a pride of lions, a charm of finches, an exaltation of skylarks . . . what is the collective noun for mathematicians? A magnificence of mathematicians? Too smug. A mystification of mathematicians? Too close to the mark. Having had many opportunities to observe the behavior of the mathematical species when congregated in large herds, I think that the most apt word is “muddle.”

One such muddle invented one of the most bizarre structures in the entire subject, and discovered a hidden unity behind its puzzling facade. Their discoveries, mainly obtained by pottering around and seeing what turned up, are beginning to infiltrate theoretical physics, and they may just hold the key to some of the more curious features of superstrings.

The mathematics of superstrings is so new that most of it has not been invented yet. But ironically, mathematicians and physicist have just discovered that superstrings, at the frontiers of modern physics, seem to have a curious relationship to a bit of Victorian algebra so old-fashioned that it is seldom mentioned in university mathematics courses. This algebraic invention is known as the octonions, and it is the next structure in line after real numbers, complex numbers, and quaternions.

Octonions were discovered in 1843, published by someone else in 1845, and ever afterward credited to the wrong person—but that didn't matter, since nobody took any notice. By 1900 they had fallen into obscurity even in mathematics. They experienced a brief revival in 1925 when Wigner and von Neumann tried to make them the basis of quantum mechanics, but then fell back into obscurity when the attempt failed. In the 1980s they resurfaced as a potentially useful gadget in string theory. In
1999 they turned up as a crucial ingredient in 10- and 11-dimensional superstring theory.

Octonions tell us that there is something very strange about the number 8, and something even stranger about the physics of space, time, and matter. A Victorian whimsy has been reborn as the key to deep mysteries on the common frontier of mathematics and physics—especially the belief that space-time may have more dimensions than the traditional four, and that this is how gravity and quantum theory fit together.

The tale of the octonions lives in the heady realms of abstract algebra, and it is the topic of a beautiful mathematical survey published in 2001 by the American mathematician John Baez. I have drawn heavily on Baez's insights here. I'll do my best to convey the bizarre yet elegant wonders that inhabit this curious interface between mathematics and physics. As with the ghost of Hamlet's father, a disembodied voice beneath the stage, much of the mathematical action must happen out of sight of the audience. Bear with me, and don't worry too much about the odd piece of unexplained jargon. Sometimes we just need a convenient word to keep track of the main players.

A few reminders may help to set the scene. The step-by-step expansion of the number system has woven in and out of our tale of the quest for symmetry. The first step was the discovery (or invention) in the mid-sixteenth century of complex numbers, in which –1 has a square root. Until that time, mathematicians had thought that numbers were God-given, unique, and
done.
No one could contemplate inventing a new number. But around 1550, Cardano and Bombelli did just that, by writing down the square root of a negative number. It took about 400 years to sort out what the thing meant, but only 300 to convince mathematicians that it was too useful to be ignored.

By the 1800s, Cardano and Bombelli's baroque concoction had crystallized into a new kind of number, with a new symbol:
i
. Complex numbers may seem weird, but they turn out to be a marvelous tool for understanding mathematical physics. Problems of heat, light, sound, vibration, elasticity, gravity, magnetism, electricity, and fluid flow all succumb to the complex weaponry—but only for physics in two dimensions.

Our own universe, however, has three dimensions of space—or so we thought until recently. Since the two-dimensional system of complex
numbers is so effective for two-dimensional physics, might there be an analogous three-dimensional number system that can be used for genuine physics? Hamilton spent years trying to find one, with absolutely no success. Then, on 16 October 1843, he had a flash of insight:
don't look in three dimensions, look in four
, and carved his equations for quaternions into the stonework of Brougham Bridge.

Hamilton had an old friend from college, John Graves, who was an algebra buff. It was probably Graves who got Hamilton excited about extensions of the number system in the first place. Hamilton wrote his buddy a long letter about quaternions the day after he had vandalized the bridge. Graves was initially perplexed, and wondered how legitimate it was to invent multiplication rules off the top of one's head. “I have not yet any clear views as to the extent to which we are at liberty arbitrarily to create imaginaries, and to endow them with supernatural properties,” he wrote back. But he also saw the potential of the new idea and wondered how far it might be pushed: “If with your alchemy you can make three pounds of gold, why stop there?”

It was a good question, and Graves set about answering it. Within two months he wrote back to say that he had found an
eight
-dimensional number system. He called it the “octaves.” Associated with it was a remarkable formula about sums of eight squares, to which I will shortly return. He tried to define a 16-dimensional number system, but met what he called an “unexpected hitch.” Hamilton said that he would help to bring his friend's discovery to public attention, but he was too busy exploring quaternions to do so. Then he noticed a potential embarrassment: multiplication of octaves does not obey the associative law. That is, the two ways to form products of three octaves, (
ab
)
c
and
a
(
bc
), are usually
different.
After much soul-searching, Hamilton had been willing to dispense with the commutative law, but throwing away the associative law might be going too far.

Now Graves had some serious bad luck. Before he could publish, Cayley independently made the same discovery, and in 1845 he published it as an addendum to an otherwise awful paper on elliptic functions—so riddled with errors that it was removed from his collected works. Cayley called his system “octonions.”

Graves was unhappy at being beaten to publication, and it so happened that a paper of his own was shortly due to be published in the journal
where Cayley had announced his discovery. So Graves added a note to his paper, pointing out that he had come across the same idea two years before, and Hamilton backed him up by publishing a brief note confirming that his friend should be granted priority. Despite the record being set straight, the octonions quickly acquired the name “Cayley numbers,” which is still widely used. Many mathematicians now use Cayley's terminology, calling the system “octonions,” but give credit to Graves. It's a better name than “octaves” anyway, because it resembles “quaternions.”

The algebra of octonions can be described in terms of a remarkable diagram known as the Fano plane. This is a finite geometry composed of seven points joined in threes by seven lines, and it looks like this:

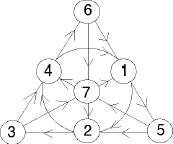
The Fano plane, a geometry with seven points and seven lines.

One line has to be bent into a circle to draw it in the plane, but that doesn't matter. In this geometry, any two points are joined by a line, and any two lines meet at a point. There are no parallel lines. The Fano plane was invented for a totally different purpose, but it turned out to encapsulate the rules for multiplying octonions.