Why Beauty is Truth (37 page)
Read Why Beauty is Truth Online
Authors: Ian Stewart

The most significant meeting, however, was in Berlin with Felix Kleinâwho, it happened, had been a student of Plücker, whom Lie greatly admired and wished to emulate. Lie and Klein had very similar mathematical backgrounds, but their tastes differed considerably. Klein, basically an algebraist with geometrical leanings, enjoyed working on special problems with inner beauty; Lie was an analyst who liked the broad sweep of general theories. Ironically, it was Lie's general theories that gave mathematics some of its most important special structures, which were and still are extraordinarily beautiful, extraordinarily deep, and mostly algebraic. These structures might not have been discovered at all were it not for Lie's push to generality. If you try to understand all possible mathematical objects of a certain kind, and succeed, you will inevitably find many that have unusual features.
In 1870, Lie and Klein met again in Paris. And there, Jordan converted Lie to the cause of group theory. There was a growing realization that geometry and group theory were two sides of the same coin, but it took a long time for the idea to become fully formed. Lie and Klein did some joint work, trying to make the connection between groups and geometry more explicit. Eventually, Klein crystallized the thought in his “Erlangen Program” of 1872, according to which geometry and group theory are identical.
In modern language, the idea sounds so simple that it should have been obvious all along. The group that corresponds to any given geometry is the
symmetry group
of that geometry. Conversely, the geometry corresponding to any group is whatever object it is the symmetry group
of.
That is, the geometry is defined by those things that are invariant under the group.
For example, the symmetries of Euclidean geometry are those transformations of the plane that preserve lengths, angles, lines, and circles. This is the group of all rigid motions of the plane. Conversely, anything that is invariant under rigid motions naturally falls within the purview of Euclidean
geometry. Non-Euclidean geometry simply employs different transformation groups.
Why, then, bother converting geometry into group theory? Because it gives you two different ways to think about geometry, and two different ways to think about groups. Sometimes one way is easier to understand, sometimes the other. Two points of view are better than one.

Relations between France and Prussia were deteriorating fast. Emperor Napoleon III thought he could shore up his declining popularity by starting a war with Prussia. Bismarck sent the French a stinging telegram, and the Franco-Prussian War was declared on 19 July 1870. Klein, a Prussian in Paris, deemed it prudent to head back to Berlin.
Lie, however, was Norwegian and was greatly enjoying his visit, so he decided to stay in Paris. But he changed his mind when he realized that France was losing the war and the German army was advancing on Metz. Although he was a citizen of a neutral country, it was not safe to remain in a potential war zone.
Lie decided to go on a hiking trip, heading for Italy. He did not get far; the French authorities caught him at Fontainebleau, about 25 miles southeast of Paris, carrying a number of documents covered in incomprehensible symbols. Since these were evidently in code, Lie was obviously spying for the Germans, and he was placed under arrest. It took the intervention of a leading French mathematician, Gaston Darboux, to convince the authorities that the writings were mathematics. Lie was let out of prison, the French army surrendered, the Germans began a blockade of Paris, and Lie once more headed for Italyâthis time successfully. From there he returned to Norway. Along the way he dropped in on Klein, who had remained safe in Berlin.
Lie received his doctorate in 1872. The Norwegian academic world was so impressed by his work that the University of Christiania created a position especially for him in the same year. With his former teacher Ludwig Sylow, he took on the task of editing Abel's collected works. In 1874 he married Anna Birch, eventually fathering three children.
By now, Lie had focused on a particular topic that he felt was ripe for development. There are many kinds of equations in mathematics, but two types are especially important. The first is algebraic equations, of the kind
studied so effectively by Abel and Galois. The second is differential equations, introduced by Newton in his work on the laws of nature. Such equations involve concepts from calculus, and instead of dealing directly with some physical quantity, they describe how that quantity changes as time passes. More precisely, they specify the
rate of change
of the quantity. For example, Newton's most important law of motion states that the acceleration experienced by a body is proportional to the total force acting on it. Acceleration is the rate of change of velocity. Instead of telling us directly what the body's velocity is, the law tells us the rate of change of velocity. Similarly, another equation that Newton developed, to explain how the temperature of an object changes when it cools, states that
the rate of change
of temperature is proportional to the difference between the temperature of the object and the temperature of its surroundings.
Most of the important equations in physicsâthose that concern the flow of a fluid, the action of gravity, the motion of the planets, the transfer of heat, the movement of waves, the action of magnetism, and the propagation of light and soundâare differential equations. As Newton first realized, nature's patterns generally become simpler and easier to spot if we look at the rates of change of the quantities that we want to observe, not at those quantities themselves.
Lie posed himself a momentous question. Is there a theory of differential equations analogous to Galois's theory of algebraic ones? Is there a way to decide when a differential equation can be solved by specified methods?
The key, once more, was symmetry. Lie now realized that some of his results in geometry could be reinterpreted in terms of differential equations. Given one solution of a particular differential equation, Lie could apply a transformation (from a particular group) and prove that the result was also a solution. From one solution you could get many, all connected by the group. In other words, the group consisted of symmetries of the differential equation.
It was a broad hint that something beautiful awaited discovery. Consider what Galois's application of symmetries had done for algebraic equations. Now imagine doing the same thing for the far more important class of differential equations!

The groups studied by Galois are all finite. That is, the number of transformations in the group is a whole number. The group of all permutations on the five roots of a quintic, for example, has 120 elements. Many sensible groups are infinite, however, including symmetry groups of differential equations.
One common infinite group is the symmetry group of a circle, which contains transformations that rotate the circle through any angle whatsoever. Since there are infinitely many possible angles, the rotation group of the circle is infinite. The symbol for this group is SO(2). Here “O” stands for “orthogonal,” meaning that the transformations are rigid motions of the plane, and “S” means “special”ârotations do not flip the plane over.
Circles also have infinitely many axes of reflectional symmetry. If you reflect a circle in any diameter, you get the same circle. Adding in the reflections leads to a bigger group, O(2).
The groups SO(2) and O(2) are infinite, but it is a tame type of infinity. The different rotations can all be determined by specifying a single numberâthe relevant angle. When two rotations are composed, you just add the corresponding angles. Lie called this kind of behavior “continuous,” and in his terminology, SO(2) was therefore a continuous group. And because only one number is needed to specify an angle, SO(2) is one-dimensional. The same goes for O(2), because all we need is a way to distinguish reflections from rotations, and this is a matter of a plus or minus sign in the algebra.
The group SO(2) is the simplest example of a
Lie group
, which has two types of structure at the same time: it is a group and also a manifoldâa multidimensional space. For SO(2), the manifold is a circle, and the group operation combines two points on the circle by adding the corresponding angles.
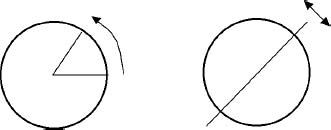
The circle has infinitely many rotational symmetries (left) and infinitely many reflectional symmetries (right).
Lie discovered a beautiful feature of Lie groups: the group structure can be “linearized.” That is, the underlying curved manifold can be replaced by a flat Euclidean space. This space is the tangent space to the manifold. Here's how it looks for SO(2):
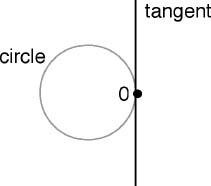
From Lie group to Lie algebra: the tangent space to a circle.
The group structure, when linearized in this fashion, gives the tangent space an algebraic structure of its own, which is a kind of “infinitesimal” version of the group structure, describing how transformations very close to the identity behave. It is called the
Lie algebra
of that group. It has the same dimension as the group, but its geometry is much simpler, being flat.
There is a price to pay for this simplicity, of course: the Lie algebra captures most important properties of the corresponding group, but some fine detail gets lost. And those properties that are captured undergo subtle changes. Nonetheless, you can learn a lot about a Lie group by passing to its Lie algebra, and most questions are more easily answered in the Lie algebra setting.
It turns outâand this was one of Lie's great insightsâthat the natural algebraic operation on the Lie algebra is not the product
AB
, but the difference
AB
â
BA
, which is called the
commutator.
For groups like SO(2), where
AB
=
BA
, the commutator is zero. But in a group like SO(3), the rotation group in three dimensions,
AB
â
BA
is nonzero unless the axes of rotation of
A
and
B
are either the same or at right angles. So the geometry of the group shows up in the behavior of commutators.