Why Beauty is Truth (34 page)
Read Why Beauty is Truth Online
Authors: Ian Stewart

For several hundred years, the possibility of giving sensible meaning to the square root of minus one had flitted in and out of the collective mathematical consciousness. No one had any idea whether such a number could exist. But they began to realize that it would be extremely useful if it did.
At first, such “imaginary” quantities had exactly one use: to indicate that a problem had no solutions. If you wanted to find a number whose square was minus one, the formal solution “square root of minus one” was imaginary, so no solution existed. No less a thinker than René Descartes made just this point. In 1637 he distinguished “real” numbers from “imaginary” ones, insisting that the presence of imaginaries signals the absence of solutions. Newton said the same thing. But both of these luminaries were reckoning without Bombelli, who had noticed centuries earlier that sometimes imaginaries signal the
presence
of solutions. But the signal is hard to decipher.
In 1673 the English mathematician John Wallis, who was born in Ashford, about fifteen miles from my hometown in the county of Kent, made a fantastic breakthrough. He found a simple way to represent imaginary numbersâeven “complex” ones that combined real numbers with imaginariesâas points in the plane. The first step is the now-familiar concept of the real “number line,” a kind of ruler extending to infinity in both directions, with 0 in the middle, the positive real numbers wandering off to the right, and the negative ones to the left.
Every real number can be located on the number line. Each successive decimal place requires a subdivision of the unit length into ten, a hundred, a thousand, etc., equal parts, but that is no problem. Numbers like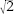 can be located as accurately as we wish, somewhere in between 1 and 2, a bit to the left of 1.5. The number Ï sits a little to the right of 3, and so on.
can be located as accurately as we wish, somewhere in between 1 and 2, a bit to the left of 1.5. The number Ï sits a little to the right of 3, and so on.
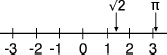
The real number line.
But where does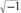 go? There is no place for it on the real number line. It is
go? There is no place for it on the real number line. It is
neither positive nor negative; it can go neither to the right nor to the left of 0.
So Wallis put it somewhere else. He introduced a second number line, to include the imaginariesâthe multiples of
i
âand placed it
at right angles
to the real number line. It was literally a case of “lateral thinking.”
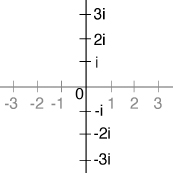
Two copies of the real number line, placed at right angles.
The two number lines, real and imaginary, have to cross at 0. It is very easy to prove that if numbers make sense at all, then 0 times
i
must equal 0, so the origins of the real and imaginary lines coincide.
A complex number consists of two parts: one real, one imaginary. To locate this number in the plane, Wallis told his readers to measure off the real part along the horizontal “real” line, and then measure off the imaginary part verticallyâparallel to the imaginary line.
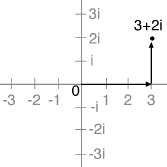
The complex plane according to Wallis.
This proposal completely solved the problem of giving meaning to imaginary and complex numbers. It was simple but decisive, a true work of genius.
It was totally ignored.

Despite the lack of public recognition, Wallis's breakthrough must have percolated into the mathematical consciousness, because mathematicians started to employ subconscious images that related directly to Wallis's basic idea: there is no complex number line, there is a complex
plane.
As mathematics became more versatile, mathematicians started trying to calculate ever more complicated things. In 1702, Johann Bernoulli, trying to solve a calculus problem, found that he needed to evaluate the logarithm of a complex number. By 1712, Bernoulli and Leibniz were doing battle over a core issue: what is the logarithm of a negative number? If you could solve that, you could find the logarithm of any complex number because the logarithm of a number's square root is just half the logarithm of that
number. So the logarithm of
i
is half that of â1. But what is the logarithm of â1?
The issue at stake was simple. Leibniz believed the logarithm of â1 had to be complex. Bernoulli said it had to be real. Bernoulli based his contention on a simple piece of calculus; Leibniz objected that neither the method nor the answer made sense. In 1749, Euler resolved the controversy, coming down heavily in favor of Leibniz. Bernoulli, he pointed out, had forgotten something. His calculus calculation was of a kind that involved the addition of an “arbitrary constant.” In his enthusiasm for complex calculus, Bernoulli had tacitly assumed that this constant was zero. It wasn't. It was imaginary. This omission explained the discrepancy between Bernoulli's answer and Leibniz's.
The pace of “complexification” of mathematics was heating up. More and more ideas originating in the study of real numbers were being extended to complex ones. In 1797, a Norwegian named Caspar Wessel published a method to represent complex numbers as points in a plane. Caspar came from a family of church ministers and was the sixth of fourteen children. At that time, Norway had no universities but was united with Denmark, so in 1761 he went to the University of Copenhagen. He and his brother Ole studied law, and Ole worked on the side as a surveyor, to stretch the family finances. Later, Caspar became Ole's assistant.
While working as a surveyor, Caspar invented a way to represent the geometry of the planeâespecially its lines and their directionsâin terms of complex numbers. Conversely, his ideas could be seen as representing complex numbers in terms of the geometry of the plane. He presented the workâhis one and only research paper in mathematicsâto the Royal Danish Academy in 1797.
Hardly any leading mathematicians read Danish, and the work languished unread until it was translated into French a century later. Meanwhile, the French mathematician Jean-Robert Argand independently had the same idea and published it in 1806. By 1811 it had occurred to Gauss, independently again, that complex numbers could be viewed as the points of a plane. The terms “Argand diagram,” “Wessel plane,” and “Gauss plane” began to circulate. Different nationalities tended to employ different phrases.
Hamilton took the final step. In 1837, almost three hundred years after Cardano's formula had suggested that “imaginary” numbers might be useful,
Hamilton removed the geometric element and reduced complex numbers to pure algebra. His idea was simple; it was implicit in Wallis's proposal and in the equivalent ideas of Wessel, Argand, and Gauss. But no one had made it explicit.
Algebraically, said Hamilton, a point in the plane can be identified with a pair of real numbers, its coordinates (
x, y
). If you look at Wallis's diagram (or Wessel's, Argand's, or Gauss's) you can see that
x
is the real part of the number and
y
is its imaginary part. A complex number
x
+
iy
is “really” just a pair of real numbers, (
x, y
). You can even lay down rules for adding and multiplying these pairs, and the main step is to observe that since
i
corresponds to the pair (0, 1), then (0, 1) Ã (0, 1) must equal (â1, 0). At this point Gauss revealed, in a letter to the Hungarian geometer Wolfgang Bolyai, that exactly the same idea had occurred to him in 1831. Once again, the fox had covered his tracksâso completely that nothing had been visible.
Problem solved. A complex number is just a pair of real numbers, manipulated according to a short list of simple rules. Since a pair of real numbers is surely just as “real” as a single real number, real and complex numbers are equally closely related to reality, and “imaginary” is misleading.
Today's view is rather different: it is that “real” is what's misleading. Both real and imaginary numbers are equally figments of human imagination.
