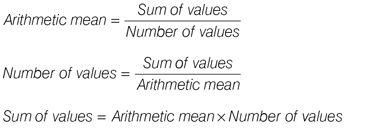How to Pass Numerical Reasoning (51 page)

If there are 20 party bags and 5 will not get any chocolates, 15 party bags will get extra chocolate.

So there are 60 chocolates to distribute among 15 party bags.

60 ÷ 15 = 4

Therefore, each party bag will receive an extra 4 chocolates.

Q6 answer
=
£8

Q6 explanation

You can solve this question using arithmetic or algebra.

Read the whole question and underline the key phrases:

The total entrance price to The Design Museum for
2 adults and 2 children
is £24. The ticket price for
a child is half the price of an adult’s ticket
. How much does an adult’s ticket cost?

Solving the question using arithmetic:
you are told that an adult’s ticket costs twice as much as a child’s ticket. So the price for 1 adult is the same as for 2 children. For 2 adults, the price is therefore the same as for 4 children. The total cost for 2 adults and 2 children is therefore the same as the total cost for 6 children.

If the entry price for 6 children is £24, then each child’s ticket costs £4. An adult’s ticket costs twice as much, or £8.

Solving the problem with algebra:
let
x
= the cost of an adult’s ticket and
y
= the cost of a child’s ticket. Set up the two equations as they are given to you in the logic problem:

You have two unknown variables and two equations, so you can solve the problem.

In Equation 2, substitute
x
for an expression in terms of
y
; so 2x = 4
y
.

4
y
+ 2
y
= 24

6
y
= 24

Divide both sides by 6.

y
= 24 ÷ 6

y
= 4

Now use the value of
y
to work out the value of
x
in equation 1.

x
= 2
y

x
= 2 × 4

x
= 8

Q7 answer
=
20%

Q7 explanation

You can solve this question using arithmetic.

Read the whole question and underline the key phrases:

There are two schools in a district. At
Child Genius, 20% of the
students are aged under 4
. At
Stepford Child, which is half the
size of its local rival, 20% of the students are aged under 4
. What
percentage
of both classes
combined
are aged under 4?

The question asks you to give an answer in terms of a percentage, so you don’t need to worry about finding a value. In a question involving percentages, the easiest way to solve for a value is to pick a number for the class size. For example, let’s say that Child Genius has 100 children.

At Child Genius, we are told that 20% are aged under 4.

20% of 100 = 20 under-4s

At Stepford Child, which is half the size of Child Genius, 20% are aged under 4. So work out 20% of 50:

10% of 50 = 5 under-4s

20% of 50 is 2 × 5 = 10 under-4s

Therefore, at Stepford Child, 10 students are aged under 4.

You are asked to find the percentage of students of both classes who are aged under 4.

In both classes combined, there are 150 children, of whom 30 are aged under 4.

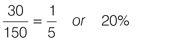
Q8 answer
=
15 advisors

Q8 explanation

You can solve this question using arithmetic.

Read the whole question and underline the key phrases:

11 ambassadors
are at a meeting in Whitehall. Some are accompanied by advisors. After a dispute over foreign policy, 5 ambassadors leave and there are three times as many advisors as ambassadors left.
A number of advisors
also leave and there remain twice as many ambassadors as advisors.
How many
advisors have left?

When 5 ambassadors leave, there are 11 – 5 = 6 ambassadors. We know that there are three times as many advisors as ambassadors, or 6 × 3 = 18 advisors.

After some advisors have left, the total number of ambassadors equals twice the number of advisors. If there are 6 ambassadors, then there must be 3 advisors remaining, so 15 must have left.

Q9 answer
=
£2,200

Q9 explanation

You can solve this question using arithmetic.

Read the whole question and underline the key phrases:

A home building’s insurance policy
pays 80%
of the cost of repairs resulting from a burglary. The policy carries a
£200
excess
. If the cost to repair windows, doors and locks is
£10,000
, how much is payable by the policyholder?

The total payable is £10,000. The insurance company will pay 80% of this.

10% of £10,000 is £1,000, so 80% of £10,000 is 8 × £1,000 = £8,000.

The rest (£2,000) is payable by the policyholder, who is also liable for the £200 excess.

Therefore, the total payable by the policyholder is £2,000 + £200 = £2,200.

The specific wording of the insurance policy will determine the actual amount payable!

Q10 answer
=
8 €10 notes

Q10 explanation

You can solve this question using algebra.

Read the whole question and underline the key phrases:

While on holiday in Italy, Jamie withdraws €200 from her bank account and receives a pile of €10 and €20 notes. How many €10 notes does Jamie receive if she receives 14 notes in total?

You are told that:

The total amount received = €200

The total number of notes = 14

There is a mix of €20 and €10 notes.

You are looking for the number of €10 notes.

Let’s call the total number of €10 notes
n
and the total number of €20 notes
m
.

You can now set up two equations with the given information:

10
n
+ 20
m
= 200

We shall call this equation 1: Jamie receives €200 in €10 and €20 notes.

n
+
m
= 14

We shall call this equation 2: the total number of notes received is 14.

Deal with equation 1 first to find an expression for
n
.

Divide both sides by 10:

10
n
+ 20
m
= 200 becomes
n
+ 2
m
= 20

Subtract 2
m
from both sides to find a value for
n
:

n
= 20 – 2
m

Now substitute this value for
n
in equation 2:

(20 – 2
m
) +
m
= 14

Subtract
m
from both sides:

20 – 2
m
= 14 –
m

Add 2
m
to both sides:

20 = 14 +
m

Subtract 14 from both sides:

6 =
m

Remember that
m
represents the number of €20 notes and you are looking for the number of €10 notes, represented by
n
. You can now insert the value for
m
into equation 2 to find the value of
n
.

n
+
m
= 14

n
+ 6 = 14

Subtract 6 from both sides:

n
= 14 – 6

n
= 8

Therefore, Jamie receives 8 €10 notes.

The progression, without the step-by-step explanation, looks like this:

10
n
+ 20
m
= 200

n
+
m
= 14

10
n
+ 20
m
= 200

n
+ 2
m
= 20

n
= 20 – 2
m

(20 – 2
m
) +
m
= 14

20 – 2
m
= 14 – m

20 = 14 +
m

6 =
m

n
+ 6 = 14

n
= 14 – 6

n
= 8

Glossary

Terms

Arithmetic mean:
The amount obtained by adding two or more numbers and dividing by the number of terms.

Compound interest:
The charge calculated on the sum loaned plus any interest accrued in previous periods.

Denominator:
The number below the line in a vulgar fraction.

Digit:
One of the numbers 0,1,2,3,4,5,6,7,8,9.

Dividend:
The number to be divided.

Divisor:
The number by which another is divided.

Equivalent fractions:
Two or more fractions with the same value.

Factor:
The positive integers by which an integer is evenly divisible.

Fraction:
A part of a whole number.

Fraction bar:
The line that separates the numerator and denominator in a
vulgar fraction
.

Improper fraction:
A fraction in which the
numerator
is greater than or equal to the
denominator
.

Integer:
A whole number without decimal or fraction parts.

Interest:
See ‘Simple interest’ and ‘Compound interest’.

Lowest common denominator:
The smallest common multiple of the denominators of two or more fractions.

Lowest common multiple:
The least quantity that is a multiple of two or more given values.

Mean:
See ‘Arithmetic mean’.

Median:
The middle number in a range of numbers when the set is arranged in ascending or descending order.

Mixed fractions:
A fraction consisting of an integer and a fraction.

Mode:
The most popular value in a set of numbers.

Multiple:
A number that divides into another without a remainder.

Multiplier:
A quantity by which a given number is multiplied.

Numerator:
The number above the line in a
vulgar fraction
.

Prime factor:
The factors of an
integer
that are
prime numbers
.

Prime factorization:
The expression of a number as the product of its
prime numbers
.

Prime number:
A number divisible only by itself and 1.

Proper fraction:
A
fraction
less than 1, where the
numerator
is less than the
denominator
.

Proportion:
Equality of
ratios
between two pairs of quantities.

Ratio:
The comparison between two or more quantities.

Simple interest:
The charge calculated on a loaned sum.

Vulgar fraction:
A fraction expressed by numerator and denominator, rather than decimally.

Formulae used in this book