How to Pass Numerical Reasoning (50 page)

CHAPTER 7

Word problems

W
hen you are presented with a word problem, it is your analytical skills that are under scrutiny as much as your numerical skills. The problem is presented in everyday language and you are expected to analyse the question, decide what is being asked of you, and translate the words into a mathematical formula, expression or equation. With practice, these types of question are quite fun and the more you practice, the more easily you will recognize hidden clues built into the question.

In previous chapters, you refreshed your memory of the basic arithmetic formulae that can help you solve common problems in a numerical reasoning test. To solve the problems in this chapter, a basic knowledge of algebra is helpful. In case you have forgotten your GCSE (or ‘O’ Level) algebra, a worked example is provided below. There is usually more than one way to solve a word problem and you may arrive at the answer in a different way if you have learnt a different method. Speed and accuracy are the key, so choose the method that helps you arrive at the right answer as quickly as possible.

Approaching a word problem

Always read the question to the end to work out what is being asked of you, and then identify the facts that will lead you to the answer. A word problem might look something like this:
Q
If Ethan had three times as many jigsaw puzzles, he would have four jigsaw puzzles less than Meredith. If Ethan had five times as many jigsaw puzzles, he would have two jigsaw puzzles less than Meredith. How many puzzles does Ethan have?

Let’s analyse the three sentences that together make up the problem. The question is at the end: ‘How many puzzles does Ethan have?’ Let’s give that number a symbol, and call it E.

There are two statements of fact that will help to solve the problem, each saying something about Ethan’s puzzles in relation to Meredith’s puzzles. We don’t yet know how many puzzles Meredith has, so let’s give that number a symbol too, and call it M.

The statement ‘If Ethan had three times as many jigsaw puzzles, he would have four jigsaw puzzles less than Meredith’ can be broken down and written in a form of shorthand like this, using symbols:

We can use the symbols to create two equations to represent the two statements in the question. From the first statement (‘If Ethan had three times as many jigsaw puzzles, he would have four jigsaw puzzles less than Meredith’), we can say: 3E = M – 4

We shall call this Equation 1.

From the second statement, ‘If Ethan had five times as many jigsaw puzzles, he would have two jigsaw puzzles less than Meredith’, we can say: 5E = M – 2

We shall call this Equation 2.

Now we have two equations and can use them to find values for E and M. Remember that an equation has a left-hand side (LHS) and a right-hand side (RHS), separated by the equals sign (=), and whatever you do to one side of the equation you must also do to the other.

We’ll deal with Equation 1 first to find an expression for M.

Add 4 to both sides
:

3E + 4 = M can be rearranged as M = 3E + 4

Now substitute this value for M in Equation 2:

5E = M – 2 becomes 5E = (3E + 4) – 2

5E = 3E + 2 becomes (+ 4 – 2 = + 2)

Subtract 3E from both sides
:

2E = 2 LHS: 5E – 3E = 2E; RHS: 3E – 3E cancels

Divide both sides by 2
:

E = 1

Remember to check your answers. Are both equations satisfied if you put in this value for E? Do they both give the same value for M?

Practice test

Q1
At Snappy Prints, it costs £5.75 to print the first photo and £1.25 for each additional photo. Next door at Happy Snappy, it costs £2.50 to print the first photo and £1.95 for each additional photo. By how much cheaper is it to print 6 photos at the less expensive photo shop?

Q2
During a five-day production cycle starting on Monday and ending on Friday, Max’s shampoo company fills exactly twice as many bottles of shampoo as the day before. By Friday evening, there are 6,200 bottles of shampoo ready for delivery. How many bottles did Max fill on Wednesday?

Q3
In the Egyptian Noughts & Crosses Competition, the two top teams, Team Noughty and Team Cross, play 320 games. After each team has played half of their games, Team Noughty has won 120 games and Team Cross has won 98 games. If Team Noughty wins half of its remaining games, how many more games must Team Cross win to exceed Team Noughty’s end-of-season score?

Q4
Marley’s monthly salary is £300 less than Catherine’s. Her monthly salary is £400 more than Tom’s. If Tom earns £2,700 per month, how much does Marley earn per month?

Q5
If all the chocolates in a box are distributed among 20 party bags, 12 chocolates will go into each party bag. If 5 partygoers don’t like chocolate and their chocolates are distributed among those who do, how many more chocolates can be added to each of the other party bags?

Q6
The total entrance price to The Design Museum for 2 adults and 2 children is £24. The ticket price for a child is half the price of an adult’s ticket. How much does an adult’s ticket cost?

Q7
There are two schools in a district. At Child Genius, 20% of the children are aged under 4. At Stepford Child, which is half the size of its local rival, 20% of the students are aged under 4. What percentage of both classes combined are aged under 4?

Q8
11 ambassadors are at a meeting in Whitehall. Some are accompanied by advisors. After a dispute over foreign policy, 5 ambassadors leave and there are three times as many advisors as ambassadors left. A number of advisors also leave and there remain twice as many ambassadors as advisors. How many advisors have left?

Q9
A home buildings insurance policy pays 80% of the cost of repairs resulting from a burglary. The policy carries a £200 excess. If the cost to repair windows, doors and locks is £10,000, how much is payable by the policyholder?

Q10
While on holiday in Italy, Jamie withdraws €200 from her bank account and receives a pile of €10 and €20 notes. How many €10 notes does Jamie receive if she receives 14 notes in total?

Practice test answers and explanations

Q1 answer
=
25p

Q1 explanation

You can solve this question using arithmetic.

Read the whole question and underline the key phrases:

At Snappy Prints, it costs
£5.75 to print the first photo
and
£1.25 for each additional photo
. Next door at Happy Snappy, it costs
£2.50 to print the first photo
and £1.95 for each additional photo. By how much cheaper is it to print
6 photos
at the less expensive photo shop?

You need to work out the difference between the total spent at each shop. Each shop charges an initial amount plus an increment. Snappy Prints charges £5.75 for the first photo and Happy Snappy charges £2.50, so you must add this amount to the cost of 5 additional photos.

At Snappy Prints, the total price is £5.75 + (5 × £1.25) = £12

At Happy Snappy, the total price is £2.50 + (5 × £1.95) = £12.25

The difference is £12.25 – £12.00 = 25p, so it is 25p cheaper to print 6 photos at Snappy Prints.

Q2 answer
=
800 bottles

Q2 explanation

You can solve this question using algebra.

Read the whole question and underline the key phrases:

During a
five-day production cycle
starting on Monday and ending on Friday, Max’s shampoo company fills exactly
twice
as many
bottles of shampoo
as the day before
. By Friday evening, there are
6,200
bottles of shampoo ready for delivery.
How many bottles did Max fill on Wednesday?

Let’s say that on Monday, Max fills
x
number of bottles.

On Tuesday, he fills 2
x
bottles.

On Wednesday, he fills 4
x
bottles.

On Thursday, he fills 8
x
bottles.

On Friday, he fills 16
x
bottles.

In total, Max fills
x
+ 2
x
+ 4
x
+ 8
x
+ 16
x
bottles = 31
x
bottles.

On Monday, Max fills
x
bottles, so work out the value of
x
.

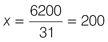
Therefore, on Wednesday, Max filled 4
x
bottles or 4 × 200 = 800 bottles.

Q3 answer = 103 games

Q3 explanation

You can solve this question using arithmetic.

Read the whole question and underline the key phrases:

In the Egyptian Noughts & Crosses Competition, the top two teams,
Team Noughty and Team Cross, play 320 games
. After each team has played half of their games,
Team Noughty has
won 120 games
and
Team Cross has won 98 games
. If Team Noughty wins half of its remaining games,
how many more
games must Team Cross
win to exceed Team Noughty’s end-of-season score?

You need to separate out the facts concerning Team Noughty and Team Cross. Team Noughty and Team Cross have each played half the total number of games, so there are 160 games left. If Team Noughty wins half of their remaining 160 games, they will have won an additional 80 games, making a total for the season of 80 + 120 = 200 games. Team Cross has won 98 games, so will need to win 103 games in order to beat Team Noughty at the end of the season (98 + 103 = 201).

Q4 answer
=
£2,800

Q4 explanation

You can solve this question using algebra or arithmetic.

Read the whole question and underline the key phrases:

Marley’s
monthly
salary is £300 less than Catherine’s
. Her monthly salary is
£400 more than Tom’s
. If Tom
earns £2,700
per month, how much does
Marley
earn per month?

Note that you are looking for
Marley’s
salary, not
Catherine’s
.

Solving the problem with arithmetic:
start with Tom’s salary, since this is a fixed value. Tom earns £2,700 per month. If Catherine earns £400 more than Tom, then Catherine earns £2,700 + £400 = £3,100. Marley earns £300 less than Catherine, so he earns £3,100 – £300 = £2,800.

Solving the problem with algebra:
pick symbols to represent values for Marley, Catherine and Tom:

M = Marley; C = Catherine; T = Tom

You are told that Tom earns £2,700 and Catherine earns £400 more than Tom, so you can make two equations:

T = 2,700

C = T + 400

So Catherine earns = £2,700 + £400 = £3,100.

You can now make a third equation to work out Marley’s salary:

M = C – 300

M = 3,100 – 300 = 2,800

Therefore, Marley earns £2,800.

Q5 answer
=
4 chocolates

Q5 explanation

You can solve this question using arithmetic.

Read the whole question and underline the key phrases:

If
all the chocolates
in a box are distributed among
20 party
bags
,
12 chocolates will go into each party bag
. If
5 partygoer don’t like chocolate
and their chocolates are distributed among those who do,
how many more chocolates can be added to
each of the other party bags?

You are trying to work out how many of the extra chocolates can be allocated. If 5 partygoers don’t like chocolate, there will be 5 × 12 = 60 extra chocolates to distribute.