How to Pass Numerical Reasoning (46 page)
Read How to Pass Numerical Reasoning Online
Authors: Heidi Smith

Germany has the least representation in the Parliament.
Q3
b) 38
Population | Total votes | = | Citizens | : | 1 vote |
Ireland | 3.6m | = | 1.2m | : | 1 |
In Ireland, 1.2 m are represented with one vote. If France had similar representation, it would also be entitled to 1 vote per 1.2 m. Total population in France = 57.5 m, so divide the total by 1.2.
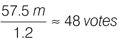
France has 10 votes, so would be entitled to a further 38 votes.
Section 5 Computer failure
Q1
c) Department C
You are asked to work out how much revenue is lost per hour per department. Divide the total weekly lost revenue by the number of hours the server is down for each department.
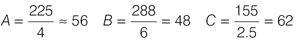
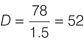
Department C loses more per hour than the other departments.
Q2
b) Department B
In each department, each employee loses the amount of time lost by the department. Employees in Department B lose the most time (6 hours.)
Q3
a) 3.5 hours
The total amount of time lost on average per week = (4 + 6 + 2.5 + 1.5) = 14 hours
Now decrease the total lost hours by 25% to find the new total:
14 × 25% = 3.5 hours.
Section 6 Survey of voting turnout in 1994 local elections
Q1
b) 7,500
The percentage of those who didn’t turn out to vote = (100% – total percentage of voting adults). In Bishopton (4 + 11 + 16 + 22 + 12 + 4) the percentage of adults who voted = 69%. So the percentage of adults who didn’t vote = 31%. The question asks you for an approximate value, so find 30% of the total: 10% × 25,100 = 2,510 so 30% × 25,100 = (10% × 3) = 7,530.
Q2
a) 3.8%
The percentage of voting adults in the 18–24 category in Thundersley = 6%.
The percentage of all voting adults in Thundersley = 64%.
6% of 64% = 0.06 × 64 = 3.8% of eligible adults who voted were aged 18–24.
Q3
b) 144
You want to find 4% of 18% of the number of adults eligible to vote in Chudleigh.
To estimate the answer find 5% × 20% of 20,000.
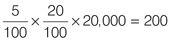
The answer choices closest to your estimate are b) 144 and c) 320. You can eliminate answers a), d) and e) at this point. To find the exact answer find 4% of 18% and multiply by 20,000: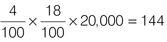
Q4
d) Thundersley
Write the percentage of voting adults in the 55–74 age category as a fraction of all voting adults in each constituency. With a rough estimate, you can see that Thundersley > Bishopton and Thundersley > Chudleigh, so eliminate Bishopton and Chudleigh. (If this doesn’t seem obvious at first, use the cross-multiplying technique you learnt in
Chapter 5
.) You are left with Thundersley and Runneymede. R =
18
⁄
74
and T =
16
⁄
64
. Reduce both fractions to their lowest terms: R =
9
⁄
37
and T = ¼. Use your knowledge of proportions to work out which is the larger of the two fractions:
Now ask ‘is 36 > 37?’ The answer is ‘no’, so Thundersley has the greatest proportion of voting adults in the 55–74 category.
Section 7 Mobile phone sales
Q1
d) 66.6%
Sales of TX-15 to males | = 125 |
Sales of TX-15 to females | = 250 |
Total sales of TX-15 | = 375 |
Therefore, % sales to females = |
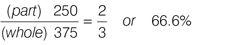
Q2
a) TX-15
Read off the graphs the ratios that tell you that fewer males bought phones than females and eliminate the rest. Only the TX-15 was sold to fewer males than to females.
Q3
d) 85
In
Figure 6.2
, read off the total number of TX-12 sales ≈ 325 + 240 = 565.
Figure 6.2
tells you that 15% of the total TX-12 sales were made to 35–49 year olds.
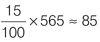
Q4
c) 96
Total MK-A1 sales in 2001 = (240 + 120) = 360. The part to part ratio of male to female sales = 240 : 120 or 2 : 1. If sales decline by 20% in 2002: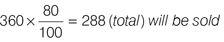
The ratio of males to females remains constant at 2 : 1. Each part = one and there are three parts. To find the ratio 2 male : 1 female, divide the total by three to find the 1 part female.
