Coming of Age in the Milky Way (49 page)

It was a hard life, waiting for years on end in lead mines and salt mines. (“That’s what they get for choosing to be
experimental
physicists,” joked one hard-hearted theorist.) The results, moreover, were null, and as years went by and no proton was observed to decay, it became increasingly evident that the GUT theorists had picked the wrong broken symmetries. Meanwhile, looking for something to do while they waited, the experimentalists put their instruments to work detecting neutrinos, a few of which betrayed their presence by smashing into atoms in the vats of water and stacks of concrete and metal that had been assembled to look for proton decay. This came in handy in 1987, when a supernova blazed forth in the Large Magellanic Cloud and a wave of neutrinos was promptly detected at the Kamioka and Lake Erie proton-decay installations. The observation confirmed a theory (authored in part by Bethe, indefatigable student of stars) that Supernovae generate enormous quantities of neutrinos, and gave birth to the new science of observational neutrino astronomy.

The waning of the grand unified theories went widely unmourned. The GUTs had lacked the sweeping simplicity that unified theories are supposed to be all about; like the standard model they were full of arbitrary parameters, and, of course, they left out
gravity. What the theorists really wanted was a “superunified” theory that would identify symmetrical family relationships among all four forces.

Elements of just such a theory began to appear, first in the Soviet Union and then independently in the West, in the 1970s. Collectively called “supersymmetry,” these new theories identified a symmetry linking bosons, the carriers of force, with fermions, the stuff of matter. Gravitation was drawn under the umbrella of the theory in 1976, a development that generated widespread excitement. And yet, by the early 1980s, supersymmetry had begun to stall. In itself it could not generate all the known quarks, leptons, and gauge particles, and it introduced even more unexplained terms than had grand unified theories and the standard model. Something was missing.

That something, a few young theorists proposed, was strings. Traditionally, elementary particles like the electron had been regarded as dimensionless points. In string theory, the particles are instead portrayed as extended objects, longer than they are wide —in short, as strings. They can be mistaken for infinitesimal objects because they are very small—only about one Planck length long, which is just about as small as anything can be. The prospect that particles are strings rather than points made an enormous difference, however, in the way their behavior was interpreted. Strings can vibrate, and the rate at which they vibrate, it turned out, can generate the properties of all known particles—and of an infinite variety of other particles as well. The bewildering diversity of the myriad particles was suddenly, if only potentially, unified, by a stroke as simple as a chord struck on Pythagoras’s lyre: All, said the theory, are but differing harmonies of strings.

String theory proffered potential answers to some of the most troubling questions that had been confronting theorists concerned with unification. Why did prior versions of quantum field theory so often generate infinities that had to be “renormalized” away? Because they regarded the elementary particles as having zero dimension: This meant they could draw infinitesimally close together, in which case the energy level of the force being exchanged between them could rise to infinity. Since strings have length, the problem of infinities did not arise in string theory. Why are gravitons spin two and the other force-carrying particles spin one? Because, said the theory, a string can either be open, meaning it has two ends,
or closed, meaning that the ends are joined, forming a loop: Open strings can be spin one, closed strings can be spin two. Why has the Yang-Mills gauge field concept enjoyed such broad applicability in understanding the forces? Because a string when in its lowest energy state—straight and nonrotating—acts like a massless, spin-one particle, and that is the description of the gauge particles that convey the Yang-Mills fields. String theory even opened a door toward understanding the conceptual gulf between relativity and quantum mechanics. Indeed, string theory could not work
without
including gravity. It was an inherently unifying conception.

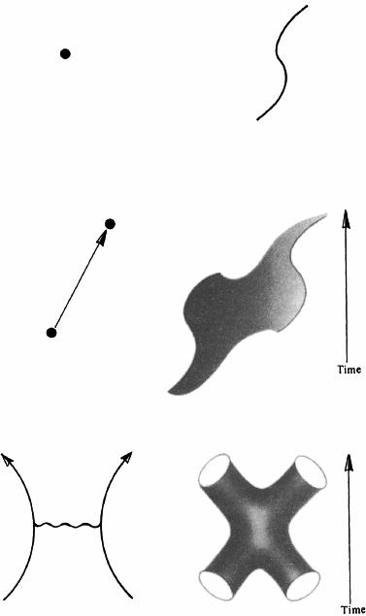
Subatomic particles, traditionally envisioned as points, are depicted in string theory as extended objects
(top)
. Particles in motion trace out world lines; strings, world sheets
(middle)
. A “Feynman diagram” of pointlike particle interactions consists of lines; for closed (i.e., looplike) strings, the Feynman diagram is tubular
(bottom)
.

The string concept originally was invoked in the 1960s, by theorists who had in mind larger strings whose harmonies might explain the behavior of the rapidly spinning hadrons. At this task it did not fare well, and most physicists soon dropped the idea. One of the few to appreciate its potential was (once again) the perspicacious Murray Gell-Mann, who encouraged the American physicist John Schwarz that even if string theory appeared sterile at present, “somehow, sometime, somewhere, it would still be useful.”
³¹

A breakthrough came in 1974, when Schwarz and the young French physicist Joel Scherk realized that an unwelcome particle that kept turning up in their string equations—its mass zero, its spin two—might be none other than the graviton, the boson that carries gravitation. Schwarz and Scherk then began thinking of strings as being only 10
⁻³⁵
meter long, the “Planck length” at which gravitation becomes as strong as the other forces and, therefore, presumably begins to function in an obviously quantized manner. Though these ideas initially garnered little enthusiasm in the scientific community, Schwarz stubbornly kept returning to the string concept, working on it in collaboration with Michael Green, who was visiting Caltech from the University of London. The concept was so unfashionable that Schwarz and Green apparently were the only two people in the world conducting research into strings at that time. But their efforts finally began to bear fruit, and in the summer of 1984 they were able to demonstrate that anomalies that had troubled other unified field theories canceled out in string theory. This captured attention, and by 1987 strings were the hottest topic in theoretical particle physics.

Writing a unified theory is something of an ad hoc affair, like
putting up a tent in a high wind; while one sets the pegs, the tent flaps free. Einstein’s relativity required abandoning classical conceptions of space and time; quantum mechanics required abridging classical causality. The odd thing about string theory was very odd indeed: It required that the universe have at least ten dimensions. As we live in a universe of only four dimensions (three of space plus one of time), the theory postulated that the other dimensions were “compactified,” meaning that they had collapsed into structures so tiny that we do not notice them. Weinberg stumped for this idea, and was kidded about it when Howard Georgi, known for his work in grand unified theory, introduced a 1984 Weinberg
lecture at Harvard by writing a limerick on the blackboard that read:

Unification of quantum mechanics and general relativity, long a conundrum, appears to be inherent to string theory. It implies that gravitation, explicated in relativity, is produced by open strings
(top)
, while the other, quantum forces are produced by closed strings
(middle)
. Cutting a closed string produces two open strings
(bottom)
, suggesting a natural affinity between the two classes of force.

Hyperdimensionality had first been introduced into unified theory by Theodor Kaluza in Germany in 1919. Kaluza wrote to Einstein, proposing that Einstein’s dream of finding a unified theory of gravitation and electromagnetism might be realized if he worked his equations in five-dimensional space-time. Einstein at first scoffed at the idea, but later reconsidered and helped Kaluza get his paper published. A few years after that, the Swedish physicist Oskar Klein published a quantum version of Kaluza’s work. The resulting Kaluza-Klein theory seemed interesting, but nobody knew what to do with it until the 1970s, when it turned out to be salutary in working on supersymmetry. Soon Kaluza-Klein was on everyone’s lips (with Gell-Mann, in his role as linguistic sentry, chiding colleagues who failed to pronounce it “Ka-woo-sah-Klein”).

Though both string theory in particular and supersymmetry in general invoked higher dimensions, strings had a way of selecting their requisite dimensionality: String theory, it soon became apparent, would work only in two, ten, or twenty-six dimensions, and invoked only two possible symmetry groups—either SO(32) or E
₈
× E
₈
. When a theory points a finger that decisively, scientists pay attention, and by the late 1980s scores were at work on strings. A great deal of toil lay ahead, but the prospects were bright. “The coming decades,” wrote Schwarz and his superstring co-workers Green and Edward Witten, “are likely to be an exceptional period of intellectual adventure.”
³³

Such optimism may, of course, prove to have been misplaced. The history of twentieth-century physics is strewn with the bleached bones of theories that were once thought to approach an ultimate answer. Einstein devoted much of the later half of his career to trying to find a unified field theory of gravitation and electromagnetism, with popular expectations running so high that equations from his work in progress were posted in windows along New
York’s Fifth Avenue, where they were scrutinized by curious if uncomprehending multitudes. Yet nothing came of it. (Einstein had ignored the quantum principle.) Wolfgang Pauli collaborated with Werner Heisenberg on a unified theory for a while, then was alarmed to hear Heisenberg claim on a radio broadcast that a unified Pauli-Heisenberg theory was close to completion, with only a few technical details remaining to be worked out. Put out by what he regarded as Heisenberg’s hyperbole, Pauli sent George Gamow and other colleagues a page on which he had drawn a blank box. He captioned the drawing with the words, “This is to show the world that I can paint like Titian. Only technical details are missing.”
³⁴

Critics of the superstring concept pointed out that claims for its power were based almost entirely upon its internal beauty. The theory had not yet so much as duplicated the achievements of the standard model, nor had it made a single prediction that could be tested by experiment. Supersymmetry did mandate that the universe ought to contain whole families of new particles, among them “selectrons” (supersymmetric counterparts of the electron) and “photinos” (counterparts of the photon), but it did not postulate the hypothetical particles’ masses. The absence of evidence adduced in preliminary searches for supersymmetric particles, like those conducted at the PEP accelerator at Stanford and at PETRA in Hamburg, therefore proved nothing; one could always imagine that the particles were too massive to be produced in these machines, or indeed in any newer and more powerful machines that might be built. The prospects of conducting experiments to test string theory were even more remote: The putative strings themselves had a theoretical mass of more than 10
²¹
times that accessible to existing accelerators, meaning that their detection, using existing technology, would require building an accelerator larger than the solar system. Supersymmetry and string theory were elegant, but if the theorists working on them had to proceed indefinitely without the benefit of what Weinberg called “that wonderful fertilization that we normally get from experiment,”
³⁵
they seemed in danger of drifting away into the ionospheric reaches of pure, abstract thought. If that happened, argued Glashow and his Harvard colleague Paul Ginsparg, their tongues only slightly in cheek, “contemplation of superstrings may evolve into an activity as remote from conventional particle physics as particle physics is from chemistry, to be conducted at schools of divinity by future equivalents of medieval
theologians.” They added sardonically that “for the first time since the Dark Ages, we can see how our noble search may end, with faith replacing science once again.”
³⁶