Coming of Age in the Milky Way (45 page)

           
T
heoretical physicists, like artists (one is tempted to say, like
other
artists) are guided in their work by aesthetic as well as rational concerns. “To make any science, something else than pure logic is necessary,” wrote Poincaré, who identified this additional element as intuition, involving “the feeling of mathematical
beauty, of the harmony of numbers and forms and of geometric elegance.”
¹
Heisenberg spoke of “the simplicity and beauty of the mathematical schemes which nature presents us. You must have felt this too,” he told Einstein, “the almost frightening simplicity and wholeness of the relationship which nature suddenly spreads out before us.”
²
Paul Dirac, the English theoretical physicist whose relativistic, quantum mechanical description of the electron ranks with the masterpieces of Einstein and Bohr, went so far as to maintain that “it is more important to have beauty in one’s equations than to have them fit experiment.”
^3
*

Aesthetics are notoriously subjective, and the statement that physicists seek beauty in their theories is meaningful only if we can define beauty. Fortunately this can be done, to some extent, for scientific aesthetics are illuminated by the central sun of
symmetry
.

Symmetry is a venerable and all but bottomless concept, with many implications in both science and art; long after the Chinese-American physicist Chen Ning Yang had won a Nobel Prize for his work in developing a symmetry theory of fields, he was still pointing out that “we do not yet comprehend the
full scope
of the concept of symmetry” (Yang’s italics).
⁴
In Greek, the word means “the same measure”
(sym
, meaning “together,” as in
symphony
, a bringing together of sounds, and
metron
, for “measurement”); its etymology thus informs us that symmetry involves the repetition of a measurable quantity. But by symmetry the Greeks also meant “due proportion,” suggesting that the repetition involved ought to be harmonious and pleasing; this suggests that a symmetrical relationship is to be judged by a higher aesthetic criterion, an idea to which I will return at the end of this chapter. In twentieth-century science, however, the former aspect of the old definition is emphasized; symmetry is said to exist when a measurable quantity remains
invariant
(meaning unchanging) under a
transformation
(meaning an alteration). Because this definition is the most relevant
to the subject at hand, I will employ it in discussing all aspects of symmetry, including those that were in general use before there was such a thing as science.

Most of us were first introduced to symmetry through its visual manifestations in geometry and art. When we say, for instance, that a sphere is rotationally symmetrical, we indicate that it possesses
a characteristic—in this case, its circular silhouette—that remains invariant throughout the transformation introduced by rotating it. The sphere can be rotated on any axis and to any degree without changing its silhouette, which makes it more symmetrical than, say, a cylinder, which enjoys a similar symmetry only when rotated on its long axis; if rotated on its short axis, the cylinder shrinks to a circle. Translational symmetries, like those found in palm fronds and building facades like that of the Doge’s Palace in Venice, occur when a shape remains invariant when moved (“translated”) a given distance along one axis. (See previous page.)

Symmetries are commonplace in sculpture, beginning with the human nude, which is (approximately) bilaterally symmetrical when viewed from the front or back, and in architecture, as in the cross-shaped floor plans of medieval cathedrals, and they turn up elsewhere in everything from weaving to square dancing. There are many symmetries in music. Bach, in the following passage from the
Toccata and Fugue in E Minor
, moves little tentlike trios of notes up and down the staff. Except for the occasional difference in a note here and there, the construct is translationally symmetrical: If we were to peel off any one trio and lay it over another, it would fit perfectly:

The first two bars of Claude Debussy’s
Deux Arabesques
are bilaterally symmetrical both within themselves and relative to each other: The sheet music can be folded vertically at the bar, or midway within each bar, and the notes will still fit atop one another:

Beneath these visible and audible manifestations of symmetry lie deeper mathematical invariances. The spiral patterns found inside the chambered nautilus and on the faces of sunflowers, for instance, are approximated by the Fibonacci series, an arithmetic operation in which each succeeding unit is equal to the total of the preceding two (1, 1, 2, 3, 5, 8 …). The ratio created by dividing any number in such a series by the number that follows it approaches the value 0.618
^*
(see page 306). This, not incidentally, is the formula of the “golden section,” a geometrical proportion that shows up in the Parthenon, the
Mona Lisa
, and Botticelli’s
The Birth of Venus
, and is the basis of the octave employed in Western music since the time of Bach. All the fecund diversity of this particular symmetry, expressed in myriad ways from seashells and pine cones to the
Well-Tempered Clavier
, therefore derives from a single invariance, that of the Fibonacci series. The realization that one abstract symmetry could have such diverse and fruitful manifestations occasioned delight among Renaissance scholars, who cited it as evidence of the efficacy of mathematics and of the subtlety of God’s design. Yet it was only the beginning. Many other abstract
symmetries have since been identified in nature—some intact and some “broken,” or flawed—and their effects appear to extend to the very bedrock foundations of matter and energy.

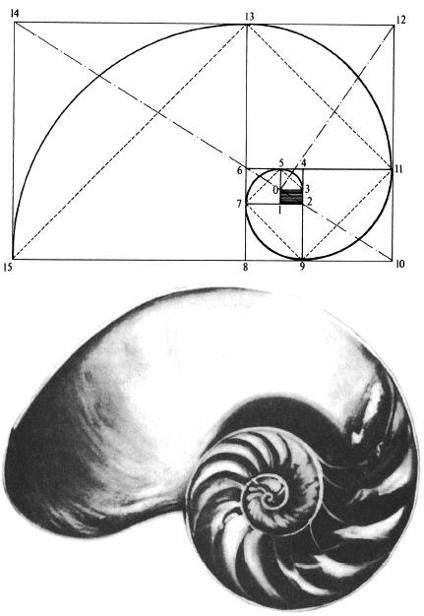
The Fibonacci series, represented in the abstract
(above)
is embodied in the architecture of the chambered nautilus
(below)
.

Which brings us back to science. When mathematicians in the early twentieth century began to look more closely at the concept of symmetry, they realized that the laws that science finds in nature are expressions of invariances—and may, therefore, be based on symmetries. This first became evident with regard to the conservation laws: The laws of thermodynamics, for instance, identify a quantity (energy) that remains invariant under a transformation (work). The German mathematician Emmy Noether demonstrated in 1918 that every conservation law implies the existence of a symmetry. The same evidently is true of the other laws as well. As the Hungarian physicist Eugene Wigner put it, “Laws of nature could not exist without principles of invariance,”
⁶
and invariance, keep in mind, is the signature of symmetry.

If natural laws express symmetries, then one ought to be able to search for previously unknown laws by looking for symmetrical relationships (invariances) in nature. Einstein absorbed this lesson in his bones, and employed symmetry as a lamp to guide his way in the creation of new theories. In special relativity (which, we recall, he originally called “invariance theory”), he employed the Lorentz transformations to maintain the invariance of Maxwell’s field equations for observers in motion; in the general theory of relativity he did much the same thing for observers in strong gravitational fields. As his friend Wigner remarked in 1949, speaking at a Princeton celebration in Einstein’s honor, “It is now natural for us to try to derive the laws of nature and to test their validity by means of the laws of invariance, rather than to derive the laws of invariance from what we believe to be the laws of nature.”
⁷

If the symmetry concept was powerful in relativity, it proved to be even more so when applied to the quantum physics of particles and fields. We can appreciate why this would be the case if we consider that subatomic particles of a given variety are indistinguishable from one another. All protons are identical. So are all neutrons and electrons. The same is true of fields; if we have two electromagnetic or gravitational fields with the same quantum numbers, and a trickster switches them while our backs are turned, we can never tell that we have been tricked, for the fields are identical. Inasmuch as identity is a form of invariance, we can, therefore,
choose to regard the individual electron or photon as representative of a symmetry group that embraces all its fellow particles of the same species. Moreover, we can look for larger symmetries that might link the various groups involved—revealing, say, a previously undiscerned invariance linking photons and electrons.

This, much simplified, is the basic concept behind unified field theory, and it is no mere intellectual exercise: Wigner, for one, found that by applying relativistic invariances to quantum mechanics he could organize all known subatomic particles into symmetry groups, classifying them according to their rest mass and their spin. An even more dramatic example of the pathfinding power of symmetry came in 1928, when Dirac derived the relativistic quantum equation of the electron, preserving the symmetries of both special relativity and quantum mechanics, and found that his equation mandated the existence of a positively charged electron. This was the first intimation that there might be such a thing as
antimatter
, particles with mass and spin identical to those of ordinary matter, but with opposite electrical charge.