125 Physics Projects for the Evil Genius (28 page)
Read 125 Physics Projects for the Evil Genius Online
Authors: Jerry Silver

Figure 43-2
Ping pong ball levitated by Bernoulli’s principle
.
According to Bernoulli’s principle,
moving air
results in
lower pressure
.
Center of mass. How to balance a broom
.
Experience tells us that objects are more stable if their center of mass is lower to the ground. Based on that, you might think it would be easier to balance a broom with brush side down. This experiment lets you answer whether that is the case.
- meterstick
- 2 books (physics textbooks are preferred, but English textbooks work almost as well)
- duct tape
- alternative: you can do this with an actual broom or any other object that has much of its mass concentrated at only one end. This can be done with modeling clay attached to the end of a broom or pencil.
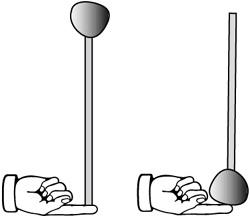
Figure 44-1
Which is easier to balance
?
- Insert the meterstick between the two books, so an inch or two of the meterstick protrudes beyond the bottom of the book.
- Secure the book to the meterstick.
- Predict which end of the meterstick you should support to most easily balance it: the heavy end or the light end?
- Support the meterstick on the heavy end.
- Try this with the heavy end up and the light end supported by your hand.
One might say that with the mass at the bottom, the meterstick will be more stable. The logic is, like with a drag racer, placing the center of gravity at the lowest point possible results in the greatest stability. The results of trying this, however, reveal the opposite to be the case. It is easier to balance the meterstick with the weight at the top, not the bottom.
The reason for this unexpected behavior is that a small movement at the support end creates a greater torque with most of the weight located at the opposite end. This gives the person trying to balance the meterstick greater control. This
principle is used by tightrope walkers who carry a pole with a weight at the end to help establish balance.
Skyscrapers are often subjected to vibration when they’re exposed to wind. Sometimes, adding mass to the structure can damp down the extent of the swaying. Apply the results of this investigation to determine whether it is more advantageous to add mass to the top floor or to the first floor of a skyscraper. Look up a specific example of how mass was added to the top, rather than the bottom, of the Sears Tower in Chicago.
Adding mass away from the pivot point increases the torque produced at the other end. This provides a greater degree of control to the end without the weight.
A simple challenge. Move your fingers to the center of a meterstick
.
OK. Here is another simple challenge: Get a meterstick. Place one finger near the 15 cm mark and the other finger near the 65 cm mark. Move both fingers together at approximately the same velocity, so they meet
together
at the 40 cm mark. Is that asking too much?
- meterstick
- Place the meterstick horizontally and hold with an outstretched finger from each hand.
- Place your fingers near the 15 and 65 meter markings of a meterstick (
Figure 45-1
). - Move both fingers at roughly the same velocity, so they meet at the 40 meter mark.
This does sound simple enough but this is just about impossible for most people to do. You will find you can
only
move the finger furthest from the center (the one starting at the 15 centimeter mark) until both fingers are the same distance from the center. Then, they meet close to the middle (the 50 cm mark). See
Figure 45-2
.
A lot of physics is actually in this little investigation. The force is greater on the finger furthest from the center (because there is greater
torque
trying to rotate the meterstick in that direction). The greater the force, the greater the force of friction. This results in one finger being able to move much more easily than the other.

Figure 45-1
The finger that has started on the 15 cm mark starts to move while the finger on the 65 cm mark hasn’t moved at all
.

Figure 45-2
Both fingers eventually meet at the 50 cm line
. Not
the 40 cm line
.
Try this with different starting finger positions. You may also need to convince any skeptics that one side of the meterstick does not have more friction than the other.
The further a weight is from a pivot point, the greater the force it exerts. Greater force between the surfaces in contact results in greater friction.
Center of gravity. How far can a stack of books extend beyond the edge of a table
?
You have four equal books. Each is 10 inches long. You can stack them up any way you like. How far from the edge of the table can you place the far edge of the top book, so all four books still balance over the edge of the table? This can be done by intuition or analytically. It also makes a good competition activity.
- stack of objects: bricks, blocks, books, or empty CD cases
- ruler
- Before you start, state your prediction. How far beyond the edge of the table will the four books go, so they balance without falling? See
Figure 46-1
. - Take the four books and arrange them, so the fourth object extends as far from the edge of the table as possible.
- Repeat with any other number of books. This makes a good friendly competition to see who can produce the greatest overhang.
If you have four similar objects, 10 inches long, the maximum overhang will be just under 9.4 inches. In general, if you have four objects whose length is
L
, the maximum overhang is (just under) 0.94 × L.
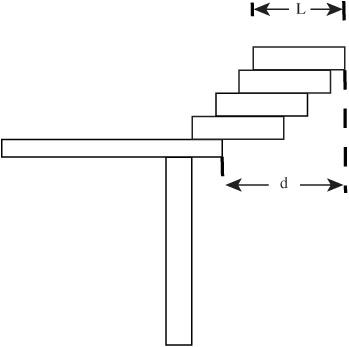
Figure 46-1
How far can the books extend beyond the edge of the table
?
The books (or other objects) will balance on the table if the center of mass for all the books lies over the table. If the center of mass is positioned over the edge of the table, the entire stack of books will topple.
Let’s start with one book. The book balances with the overhang no greater than halfway. With a second book added, the equilibrium is maintained with the added book extending one-quarter of its length beyond the first. As books are added, the added distance that the entire stack can be pushed out is one-half the length of that of the previous book, as indicated in
Figure 46-2
.
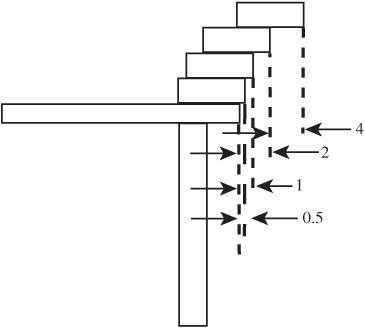
Figure 46-2
Spacing for a maximum overhang
.
Now that you got past four books, how about 100? Extending this to a large number of books, the overhang is extended by the book length divided by one-half of the total number of books.
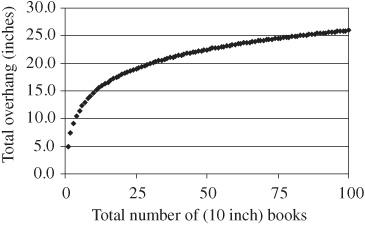
Figure 46-3
The total overhang is the sum of all the individual extensions. As an example, for 100 books, each of a length 10 inches, the maximum overhang would be 25.9 inches as pictured in
Figure 46-3
.