125 Physics Projects for the Evil Genius (54 page)
Read 125 Physics Projects for the Evil Genius Online
Authors: Jerry Silver

Figure 91-1
Courtesy PASCO
.
7. Remove the flask and immediately place it neck side down in the bucket. Hold the neck of the flask underwater as it cools. You may find it helpful to lightly insert a rubber stopper while you are transferring the flask. You can also try to use a one-hole stopper temporarily plugged with a short section of a stirring rod.
8. Once (in your judgment) it reaches equilibrium, measure the temperature of the water in the bucket. This should take less than one minute.
9. The air has contracted and some water has entered the flask. Measure the volume of the water in the flask. (The most accurate reading occurs when the air pressure about the water is in equilibrium with the outside air. This can be established by raising the bottom of the flask so that the liquid level in the flask is at the same height as the liquid level in the bucket.) See
Figure 91-2
.
10. Subtract the volume of water from the total capacity of the flask.
11. Plot the two points you measured on a graph with volume on the y-axis and temperature on the x-axis. Leave enough room on both axes so that the point where the line connecting the points extrapolates to
zero
volume fits on the graph. Draw that line and determine the temperature where the volume would be zero.
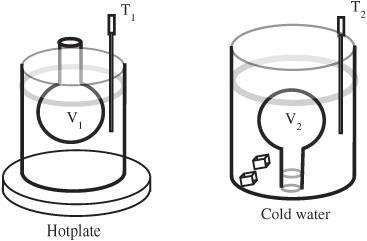
Figure 91-2
When the temperature cools from T
1
to T
2
the volume changes from V
1
to V
2
.
The accepted value for absolute zero is 0 K or −273°C or −459.7°F. However, because the first part of this experiment is a ballpark measurement, values anywhere from −175 to −350°C are reasonable extrapolations. Although this is a wide range, the concept that extrapolating the volume versus temperature curve until the volume goes to zero is significant. Statistically, we know we are on very shaky ground because we are generating data points that are far removed from the temperature we are extrapolating to.
Charles’s law
states that T
1
/V
1
= T
2
/V
2
. This can be interpreted as saying that the volume of a gas is directly proportional to the temperature. The lowest temperature conceivable is the temperature when the gas contracts to a zero volume. This can never actually occur. If we extrapolate the linear relationship between temperature and volume to zero volume, you can determine a value for absolute zero.
Similarly,
Gay-Lussac’s law
states that T
1
/P
1
= T
2
/P
2
. Absolute zero is the temperature where the temperature pressure line is extrapolated to zero pressure.
The accuracy of this measurement can be improved on by using the Gay-Lussac’s apparatus and extrapolating the temperature versus pressure curve to zero pressure, as shown in
Figure 91-3
.
Two different sets of measurements of temperature versus pressure are shown in
Figure 91-4
.
The point where the pressure extrapolates to zero is interpreted as absolute zero, as shown in
Figure 91-5
.

Figure 91-3
The Gay-Lussac apparatus is used to measure the relationship between pressure and temperature
.
One source of error in determining the change in volume with temperature is the presense of water vapor in the flask. Use of oil instead of water to immerse the flask in avoids this problem. This is a messier but more accurate way to estimate absolute zero.
Absolute zero can be determined by measuring the speed of sound at different temperatures, as described in “Determining Absolute Zero Using a Tuning Fork,” by Jeffrey D. Goldader (
The Physics Teacher
46, April 2008, 206–209).
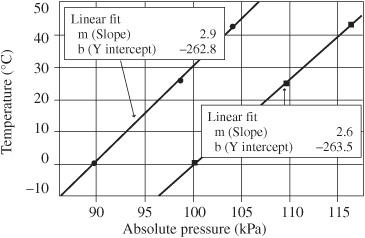
Figure 91-4
Measurement of temperature versus pressure
.
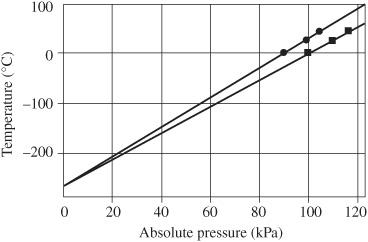
Figure 91-5
Extrapolation of temperature versus pressure data to zero pressure to find absolute zero. Courtesy PASCO
.
Absolute zero cannot be measured directly. It can be determined by extrapolating measurements of pressure versus temperature to zero pressure. Similarly, absolute zero can be determined by extrapolating measurements of volume versus temperature to zero volume.
Liquid nitrogen
.
The air we breath is about 78% nitrogen. Typically this is a gas but when brought down to an extremely cold temperature nitrogen becomes a liquid. Not only is liquid nitrogen fun to play with, but it gives you an opportunity to begin to explore low-temperature physics.
- safety goggles
- tongs and thermal mitt
- dewar (specifically designed to contain liquid nitrogen)
- sample of liquid nitrogen in a secure container
- plastic beaker
- table or other surface that will not be harmed by very cold temperatures
- Pyrex bowl large enough to hold a small quantity of liquid nitrogen and immerse the other objects listed here
- 12 inches (approximately) of lead tin or other solder wire
- 20 g hooked mass
- flowers
- banana
- hammer
- metal tube with one end open and the other sealed
- medicine bottle with easy snap on/snap off lid or a 35mm film canister
- cork that
loosely
fits into the open end of the metal tube - balloon
- Liquid nitrogen
must
be handled safely. This means it
must
be stored in a specially designed container called a
dewar
, which is intended for this purpose. Do not put liquid nitrogen in a typical lunchbox thermos, which should
never
be used for liquid nitrogen. - Liquid nitrogen is so cold, it can freeze human skin in a very short time. For all these activities, all participants should wear safety goggles and avoid any sustained contact with skin. Be especially carefully to avoid splashing liquid nitrogen, which could get trapped under clothing and cause freezing. Also, remember, objects that have been immersed in liquid nitrogen have themselves been brought to a very low temperature and should be handled appropriately.
- Carefully pour some liquid nitrogen into the Pyrex bowl.
- Using the tongs and thermal mitt, immerse the banana into the liquid nitrogen for about 15–30 seconds. Initial bubbling and vaporization diminish as the banana approaches equilibrium with the liquid nitrogen, as shown in
Figure 92-1
.

Figure 92-1
Freezing a banana in liquid nitrogen. Courtesy PASCO
.
- Remove the banana and place it on the table.
- Take the hammer and strike the banana, as shown in
Figures 92-2
and
92-3
. (For contrast, you can strike an unchilled banana either before or after, showing the effect of the much-more-brittle frozen version.)
- Using the same bowl as the previous experiment, immerse some fresh flowers in the liquid nitrogen.
- Drop the bouquet on the floor or strike them on the table.

Figure 92-2
Striking a deep-frozen banana with a hammer. Courtesy PASCO
.
