125 Physics Projects for the Evil Genius (53 page)
Read 125 Physics Projects for the Evil Genius Online
Authors: Jerry Silver

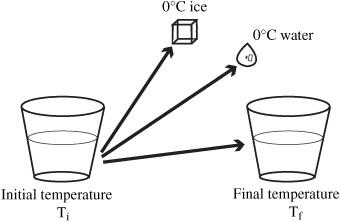
Figure 89-1
Heat is transferred
from the water
to raise the temperature of the ice and water and to melt the ice
.
– Heat extracted from the water
Given by Q
w
= m
w
C
w
(
T
f − Ti) where C
w
is the specific heat of water = 4.18J/g°C. This means that 4.18 joules of energy (which is how energy is measured) are needed to raise each gram of water every 1 degree centigrade.
– Heat needed to bring the melted ice from 0°C to the final liquid temperature
Given by Q
melted ice
= m
ice
C
w
(T
f
− 0)
– Heat needed to melt 1 gram of ice
Expected ResultsH
f
= (Q
w
– Q
melted ice
) / m
ice
The expected result is H
f
= 334 J/g. This means 334 joules of heat energy are needed to melt 1 gram of ice.
When a cube of ice is placed in a beaker of water, some heat is taken from the water. This loss of heat results in the water being brought to a lower equilibrium temperature, which is lower than the starting temperature. The heat lost by the water accomplishes two things: 1) it melts the ice, and 2) it brings the liquid resulting from the melting ice up to the equilibrium temperature. This gives the overall equation:
Q
w
= Q
melted ice
+ m
ice
H
f
Solving for H
f
gives the equation used to find the heat of fusion for ice.
Determine the temperature of a freezer. As before, place an ice cube (this time
immediately
removed from the freezer) in a Styrofoam cup filled with water of a known temperature. Do this by using the known value for the heat of fusion of ice and the heat transfer equation used previously.
Determine the temperature of a hot object (such as a red-hot nail) by measuring the temperature before and the equilibrium temperature after immersion of the object. Then solve the heat equations for the initial temperature of the object.
Calculate the amount of heat needed to melt the Greenland ice caps: Greenland contains 2.85 million cubic kilometers of ice or 1.4 × 10
14
ice cubes each with a mass of 20 g. Based on the heat of fusion for ice (0 degrees C) determined in this experiment, the Greenland ice caps would require 9.5 × 10
23
Joules of heat energy to melt.
When objects at different temperatures are mixed, they result in an equilibrium temperature that is between the highest and lowest temperatures in the mixture. The amount of heat needed to cause a certain temperature change for a given mass of material is characterized by the specific heat for that material. In addition to causing temperature change in a material, some heat (called
latent heat
) results in a change of phase from solid to liquid.
A water thermometer
.
All materials (with the one notable exception of ice at around 4°C) expand when heated. It is hard to notice the difference in volume between a hot cup of tea and the volume in the cup when the tea cools. This experiment gives a way to intensify the effect of the thermal expansion, so it can be measured and compared to a known value.
- 250 mL flask
- 2-hole rubber stopper that fits in the flask
- hotplate
- 1000 mL beaker (or one large enough for you to place the flask in)
- glass tube that fits through the rubber stopper (about 15 inches long)
- water
- glass thermometer that fits through the second hole of the stopper (if you don’t have a thermometer that works, then you need a one-hole stopper)
- Vaseline (or glycerin) and a towel to help slide the glass and the thermometer into the stopper
- ruler
- ring stand with a beaker or test tube clamp
1. Determine the radius of the glass tube by:
– Partially filling the glass tube with water.
Place your finger over the top of the tube to keep the liquid from sliding out while you are making this measurement.
– Measure the height, h
o
, of the water column.
– Release the volume into the graduated cylinder and measure the volume.
– The volume of the liquid measured V = πhr2.
– The radius of the tube is r = (V/πh
o
)
½
.
2. Carefully slide the glass tube into the stopper. Use a little Vaseline or glycerin as a lubricant and protect your hands with a towel as you push.
Don’t force it
. A few inches of the tube should extend below the stopper with the rest sticking out above.
3. Slide the thermometer into the other hole, so the bottom of the thermometer is positioned near the center of the flask.
4. Completely fill the flask with water. (Add food coloring if you like—your choice of color.)
5. Insert the stopper. A small amount of liquid may spill out over the side of the flask and some may be forced up the tube.
6. Place the flask with the stopper in the beaker.
7. Fill the beaker with water to cover the flask.
8. Place the beaker on the hot plate.
9. Turn on the hotplate. The apparatus for this experiment is pictured in
Figure 90-1
.
10. Record the temperature in the flask and note the position of the liquid in the glass tube. (If you have a Sharpie handy, mark it on the glass.)
11. When the temperature in the flask rises a few degrees, record the temperature and measure the increase in the height of the liquid in the flask.
12. The
increase in volume
for a given temperature increase is given by V = πhr
2
, where
h
is the measured height (in meters) and
r
is the inner radius of the glass previously. In setting this up, some liquid likely will extend into the tube at your starting temperature. If this is the case, define this as your zero point and
take
h
as the distance the liquid rises into the tube
. (The small difference in volume resulting from the liquid that initially rises into the tube is not significant for this measurement, but if you are very picky, you can correct for this on principle.)
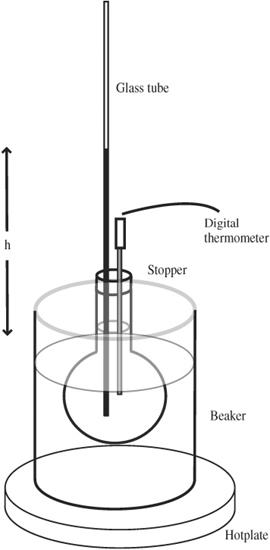
Figure 90-1
Water thermometer
.
A given volume of water expands by a factor that is 0.000207 (or 2.07 × 10
−4
) of its original volume for every 1 degree increase centigrade. This volume is distributed between the flask and the tube.
Nearly all materials expand when they are heated. The amount of expansion is characterized by something called the
coefficient of expansion
. In the case of solids, the expansion in one direction is called the coefficient of
linear
expansion. Multiplying the original length by the coefficient of linear expansion gives how much longer the object is.
Volume works almost the same way, except in the three dimensions. The
coefficient of volume expansion
indicates how much volume is added to a (solid or liquid) material for every degree the temperature increases.
Design and calibrate a water thermometer using the coefficient of volume expansion for water and the dimensions you determined for the glass tube.
The amount a material expands when heated is called the
coefficient of volume expansion
. We constrained the expansion of a larger volume of water in the flask to primarily one dimension in the tube. This magnified the effect of the expansion, so we were able to measure it.
What is the coldest possible temperature? Estimating absolute zero
.
What is the coldest thing possible? Some people might say it is giving a physics test on a Friday afternoon before winter break. (Now that’s cold!) But, the coldest temperature possible is absolute zero. This experiment is a nice, simple way to estimate this fundamental property of nature. With some extra care, a more accurate value can be obtained. We know that matter contracts as it gets cold. The basic idea here is to determine what would be the temperature if the volume were to contract to the point where it approached zero. We can’t get to that point. In fact, we can’t even get close in an ordinary lab. But, we can measure how much the volume changes for a given change in temperature and make a graph to determine at what temperature the volume would be zero. That temperature is
absolute zero
.
- 250 mL Pyrex flask
- pair of tongs suitable for safely handling a hot flask
- beaker (large enough to fully immerse the flask)
- hotplate
- thermometer
- bucket
- graduated cylinder
- A temperature volume or pressure-volume apparatus, such as shown in
Figure 91-1
.
1. Put the beaker on the hotplate.
2. Fill the beaker with water to a level that will allow the flask to be immersed without causing the water to overflow.
3. Turn on the hotplate.
4. Place the empty flask in the beaker, so it is heated from outside, but without having the heated water spill into the flask.
5. After the air in the flask has had a chance to reach equilibrium with the heated water (about 5–10 minutes at a constant temperature), measure the temperature of the water. The boiling point is a good stable measurement point, but a temperature less than this can be used if it is stable.
6. Fill the bucket with cold water. You can use ice to bring the temperature down.
