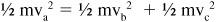125 Physics Projects for the Evil Genius (31 page)
Read 125 Physics Projects for the Evil Genius Online
Authors: Jerry Silver


Figure 50-3
The ball on the lower track picks up enough speed to move ahead of the top ball despite the extra distance. Courtesy Dan Silver
.

Figure 50-4
Both ball complete their trip at the same final velocity but with the lower ball clearly in the lead. Courtesy Dan Silver
.
The straight path is easy. The ball travels with the same constant velocity it is given at the start. It does not gain or lose energy, except for the (relatively) small loss due to friction.
On the straight section of the curved path, the second ball travels with the same velocity as the first. As it goes downhill, it picks up speed. If the shape is right, the increase in speed will be more than enough to compensate for the longer distance.
In 1696, Johann Bernoulli challenged the most brilliant minds of his day to solve what is now known as the
brachistochrone
problem—based on the Greek “brichistos” (shortest) and “chronos” (time). Basically, the problem is this: find the path between two points at different levels that an object acted on only by gravity will travel in the
least amount of time
. This is similar to the racing ball configuration previously defined, except, in this case, the balls start from rest without any initial velocity.
Galileo previously had attempted a solution to this problem. The path Galileo defined was the circular arc connecting the two points. This, although a good approximation, was
not
the correct solution.
The correct solution was found by five mathematicians who responded to Bernoulli’s challenge. This included, among others, a solution by Sir Isaac Newton, which was submitted in just one day. The path taking the shortest time was found to be a mathematical curve known as a cycloid.
A
cycloid
is defined by the equations x = r(t − sin t) and y = r(1 − cos t), where
r
can be thought of as the radius of the circle that sweeps out the cycloid and t is time.
An (inverted) cycloid generated (with r = 1,
t
varying from 0 to 3, and with
x
values as negative) is shown in
Figure 50-5
. This is actually similar to a shape generated by a pencil at the edge of circle in a Spirograph.
Although in the racing-ball scenario, we do have a slight head start in the form of an initial velocity, the cycloid curve is a good approximate minimal time path from point A to point B.
An extension to this project would be to build a track that compares a golf ball following a cycloid curve with a straight path down.
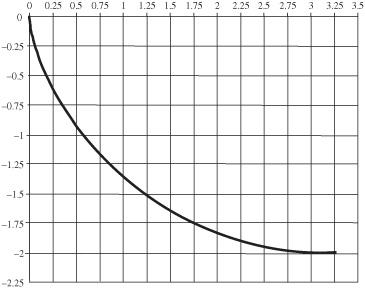
Figure 50-5
Curve shape generated by an inverted cycloid
.
Although the large track is more fun to watch, a mini version of either of these tracks can be assembled from foamboard with a track shape cut out based on the shape in
Figure 50-5
and glued to the baseboard. A clear plastic model can also work and offers the added advantage of working with an overhead projector.
A track system that can be used to study various aspects of conservation of energy can also be purchased. Two examples are shown in
Figures 50-6
and
50-7
.

Figure 50-6
Horizontal racing ball track. Courtesy PASCO
.

Figure 50-7
Brachistochrone track and straight incline. Courtesy PASCO
.
The path that takes advantage of increasing the velocity during part of the trip takes less time than one of constant velocity.
This project demonstrates that (aside from frictional losses) energy is conserved. As the potential energy is reduced, it is transformed into kinetic energy. Because both balls have returned to their original height and finished with the same velocity, we confirm that kinetic energy is conserved, regardless of the path traveled.
Linear momentum. Where can you find a perfect 90-degree angle in nature
?
Can you think of anything that forms a perfect right angle in nature? One example of a right angle is the fracture plane of body-centered cubic crystal, such as calcite. This experiment explores another example of a natural right angle that results from an elastic collision between two objects of equal mass.
- 2 low-friction objects of equal mass. Hover Pucks are excellent for this. Pennies on a smooth table can also work.
- flat, level surface
- protractor
- 2 lengths of string
- Mark the starting point of the first (stationary) puck. (Find a reasonable flat place on the floor to prevent the first puck from drifting away prematurely.)
- Place the second puck a short distance from the first one. (Do what works for you, but 18 inches may be a good starting point. If you are doing this with pennies, you probably want to shorten this to a few inches.)
- Push the second puck (the shooter) toward the stationary puck. Aim so the collision is at a glancing angle, rather than head on, hitting the stationary puck off-center as shown in
Figure 51-1
. - Mark one or more points along the path of each of the pucks after the collision. You may find a few extra sets of hands are helpful here.
- Take a piece of string and place one end at the center of the stationary puck. Place the other along the path it traveled.
- Place the other piece of string with one end also at the center of the stationary puck and the other along the path of the puck.
- Measure the angle between the two strings.

Figure 51-1
A puck (moving toward you) about to hit a stationary puck
.
Expected Results8. Get a better statistical sample by repeating this a few times and taking the average. If your collision is too direct, your angle will be zero or close to it and shouldn’t be included in your average.
The angle the two paths make should form a right triangle, as picture in
Figure 51-2
. One exception is if the moving puck hits along the centerline of the stationary puck, it may stop and send the stationary puck moving along the same path.
When two objects collide, momentum (given by mass times volume) is conserved. However, for elastic collisions, such as are being explored here, kinetic energy is
also
conserved. The only way kinetic energy can be conserved is for the colliding objects to form a perfect right triangle.
Kinetic energy is given by one-half the mass times the velocity squared (or ½mv
2
). If v
c
is the velocity of the shooter before the collision, and v
b
is the velocity of the shooter after the collision, then v
a
is the velocity of the stationary object after the collision. (There is, of course, no velocity for the stationary object before the collision because it is stationary.) Conservation of energy gives us: