Zero (17 page)

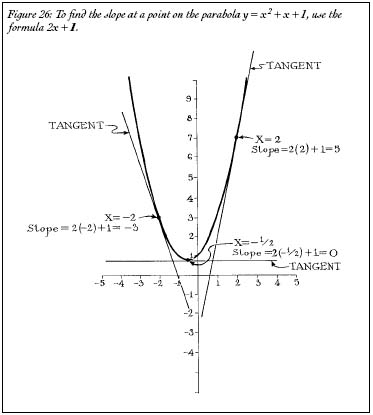
Figure 26: To find the slope at a point on the parabola y=x
²
+ x + 1, use the formula 2x + 1.

Newton's method of fluxions was very dubious. It relied upon an illegal mathematical operation, but it had one huge advantage. It worked. The method of fluxions not only solved the tangent problem, it also solved the area problem. Finding the area under a curve (or a line, which is a type of curve)—an operation we now call integration—is nothing more than the reverse of differentiation. Just as differentiating the curve
y
=
x
²
+
x
+ 1 gives you an equation for the slope of the tangent—
y
= 2
x
+ 1—integrating the curve
y
= 2
x
+ 1 gives you a formula for the area under the curve. This formula is
y
=
x
²
+
x
+ 1; the area underneath the curve between the boundaries
x
=
a
and
x
=
b
is simply (
b
²
+
b
+ 1) - (
a
²
+
a
+ 1) (Figure 27). (Technically, the formula is
y
=
x
²
+
x
+
c,
where
c
is any constant you choose. The process of differentiation destroys information, so the process of integration doesn't give you exactly the answer you are looking for unless you add another bit of information.)

Calculus is the combination of these two tools, differentiation and integration, in one package. Though Newton broke some very important mathematical rules by toying with the powers of zero and infinity, calculus was so powerful that no mathematician could reject it.

Nature speaks in equations. It is an odd coincidence. The rules of mathematics were built around counting sheep and surveying property, yet these very rules govern the way the universe works. Natural laws are described with equations, and equations, in a sense, are simply tools where you plug in numbers and get another number out. The ancients knew a few of these equation-laws, like the law of the lever, but with the beginning of the scientific revolution these equation-laws sprang up everywhere. Kepler's third law described the time it takes for planets to complete an orbit:
r
³
/
t
²
=
k
for time
t,
distance
r,
and a constant
k.
In 1662, Robert Boyle showed that if you take a sealed container with a gas in it, squishing the container would increase the pressure inside: pressure
p
times volume
v
was always a constant—
pv
=
k
for a constant
k.
In 1676, Robert Hooke figured out that the force exerted by a spring,
f,
was a negative constant, –
k,
multiplied by the distance,
x,
that you've stretched it:
f
=-
kx.
These early equation-laws were extremely good at expressing simple relationships, but equations have limitations—their constancy, which prevented them from being universal laws.

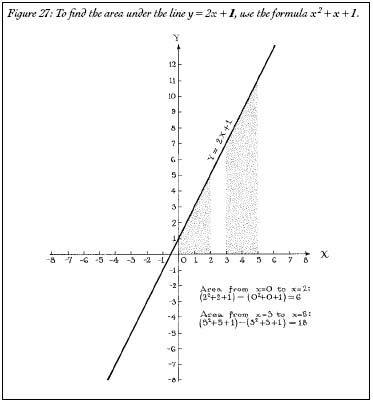
Figure 27: To find the area under the line y = 2x + 1, use the formula x
²
+ x + 1.

As an example, let's take the famous equation we all learned in high school: rate times time equals distance. It shows how far you get,
x
miles, when you run with a certain velocity,
v
miles per hour, for a time,
t
hours:
vt
=
x
; after all, miles per hour times hours equals miles. This equation is very useful when you are calculating how long it will take to get from New York to Chicago on a train that moves exactly 120 miles an hour. But how many things really move at a constant rate like a train in a math problem? Drop a ball, and it moves faster and faster; in this case,
x
=
vt
is quite simply wrong. For the case of a dropped ball,
x
=
gt
²
/2, where
g
is the acceleration due to gravity. On the other hand, if you've got an increasing force on the ball,
x
might equal something like
t
³
/3. Rate times time equals distance is not a universal law; it doesn't apply under all conditions.

Calculus allowed Newton to combine all these equations into one grand set of laws—laws that applied in all cases, under all conditions. For the first time, science could see the universal laws that underlie all of these little half laws. Even though mathematicians knew that calculus was deeply flawed—thanks to the mathematics of zero and infinity—they quickly embraced the new mathematical tools. For the truth is, nature doesn't speak in ordinary equations. It speaks in
differential equations,
and calculus is the tool that you need to pose and solve these differential equations.

Differential equations are not like the everyday equations that we are all familiar with. An everyday equation is like a machine; you feed numbers into the machine and out pops another number. A differential equation is also like a machine, but this time you feed equations into the machine and out pop new equations. Plug in an equation that describes the conditions of the problem (is the ball moving at a constant rate, or is a force acting on the ball?) and out pops the equation that encodes the answer that you seek (the ball moves in a straight line or in a parabola). One differential equation governs all of the uncountable numbers of equation-laws. And unlike the little equation-laws that sometimes hold and sometimes don't, the differential equation is always true. It is a universal law. It is a glimpse at the machinery of nature.

Newton's calculus—his method of fluxions—did just this by tying together concepts like position, velocity, and acceleration. When Newton denoted position with the variable
x,
he realized that velocity is simply the fluxion—what modern mathematicians call the derivative—of
x
:
And acceleration is nothing more than the derivative of velocity,
Going from position to velocity to acceleration and back again is as simple as differentiating (adding another dot) or integrating (removing a dot). With that notation in hand, Newton was able to create a simple differential equation that describes the motion of all objects in the universe:
F
=
m
where
F
is the force on an object and
m
is its mass. (Actually, this is not quite a universal law, as the equation only holds when the mass of an object is constant. The more general version of Newton's law is
F
=
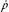where
p
is an object's momentum. Of course, Newton's equations were eventually refined further by Einstein.) If you've got an equation that tells you about the force that is being applied on an object, the differential equation reveals exactly how the object moves. For instance, if you have a ball in free fall, it moves in a parabola, while a frictionless spring wobbles back and forth forever, and a spring with friction slowly comes to rest (Figure 28). As different as these outcomes seem, they are all governed by the same differential equation.