Zero (13 page)
Authors: Charles Seife

When Blaise was twenty-three, his father slipped on a patch of ice and broke his thigh. He was cared for by a group of Jansenists, Catholics who belonged to a sect based largely on a hatred of the Jesuit order. Soon the entire Pascal family was won over, and Blaise became an anti-Jesuit, a counter-counter-reformationist. Pascal's newfound religion was not a comfortable fit for the young scientist. Bishop Jansen, the founder of the sect, had declared that science was sinful; curiosity about the natural world was akin to lust. Luckily, Pascal's lust was greater than his religious fervor for a time, because he would use science to unravel the secret of the vacuum.
About the time of the Pascals' conversion, a friend of Ãtienne'sâa military engineerâcame to visit and repeated Torricelli's experiment for the Pascals. Blaise Pascal was enthralled, and started performing experiments of his own, using water, wine, and other fluids. The result was
New experiments concerning the vacuum,
published in 1647. This work left the main question unanswered: why would mercury rise only 30 inches and water only 33 feet? The theories of the time tried to save a fragment of Aristotle's philosophy by declaring that nature's horror of the vacuum was “limited”; it could only destroy a finite amount of vacuum. Pascal had a different idea.
In the fall of 1648, acting on a hunch, Pascal sent his brother-in-law up a mountain with a mercury-filled tube. On top of the mountain, the mercury rose considerably less than 30 inches (Figure 22). Was nature somehow perturbed less by a vacuum on top of a mountain than by a vacuum in the valley?

Figure 22: Pascal's experiment
To Pascal, this seemingly bizarre behavior proved that it wasn't an abhorrence of the vacuum that drove the mercury up the tube. It was the weight of the atmosphere pressing down on the mercury exposed in the pan that makes the fluid shoot up the column. The
atmospheric pressure
bearing down on a pan of liquidâbe it mercury, water, or wineâwill make the level inside the tube rise, just as gently squeezing the bottom of a toothpaste tube will make the contents squirt out the top. Since the atmosphere cannot push infinitely hard, it can only drive mercury about 30 inches up the tubeâand at the top of the mountain, there is less atmosphere pushing down, so the air can't even push the mercury as high as 30 inches.
It is a subtle point: vacuums don't suck; the atmosphere pushes. But Pascal's simple experiment demolished Aristotle's assertion that nature abhors a vacuum. Pascal wrote, “But until now one could find no one who took thisâ¦view, that nature has no repugnance for the vacuum, that it makes no effort to avoid it, and that it admits vacuum without difficulty and without resistance.” Aristotle was defeated, and scientists stopped fearing the void and began to study it.
It was also in zero and the infinite that Pascal, the devout Jansenist, sought to prove God's existence. He did it in a very profane way.
The Divine Wager
What is man in nature? Nothing in relation to the infinite, everything in relation to nothing, a mean between nothing and everything.
âB
LAISE
P
ASCAL
,
P
ENSÃES
Pascal was a mathematician as well as a scientist. In science Pascal investigated the vacuumâthe nature of the void. In mathematics Pascal helped invent a whole new branch of the field: probability theory. When Pascal combined probability theory with zero and with infinity, he found God.
Probability theory was invented to help rich aristocrats win more money with their gambling. Pascal's theory was extremely successful, but his mathematical career was not to last. On November 23, 1654, Pascal had an intense spiritual experience. Perhaps it was the old Jansenist antiscience creed that was building up in him, but for whatever the reason, Pascal's newfound devotion led him to abandon mathematics and science altogether. (He made an exception for a brief time four years later, when he was unable to sleep owing to illness. He started doing mathematics and the pain eased. Pascal believed that this was a sign that God was not displeased with his studies.) He became a theologianâbut he could not escape his profane past. Even when it came to arguing about God's existence, he kept coming back to those crass gambling Frenchmen. Pascal argued that it was best to believe in God, because it was a good bet. Literally.
Just as he analyzed the valueâor expectationâof a gamble, Pascal analyzed the value of accepting Christ as savior. Thanks to the mathematics of zero and infinity, Pascal concluded that one should assume that God exists.
Before considering the wager itself, it is easy to analyze a slightly different game. Imagine that there are two envelopes, marked A and B. Before you are shown the envelopes, a flip of the coin determined which envelope has money in it. If the coin toss was a heads, A has a brand-new $100 bill inside. If the coin came up tails, B has the moneyâbut this time, it's $1,000,000. Which envelope should you choose?
B, obviously! Its value is much greater. It is not difficult to show this using a tool from probability theory called an
expectation,
which is a measure of how much we expect each envelope to be worth.
Envelope A might or might not have a $100 bill in it; it has some value, because it might have money in it, but it isn't worth as much as $100, because you're not absolutely sure that it contains anything. In fact a mathematician would add up all of the possible contents of envelope A and then multiply by the probability of each outcome:

The mathematician would conclude that the expected value of the envelope is $50. At the same time, the expected value of envelope B is:

So the expected value of B is $500,000â10,000 times as much as the expected value of envelope A. Clearly, if you are offered a choice between the two envelopes, the smart thing to do is to choose B.
Pascal's wager is exactly like this game, except that it uses a different set of envelopes: Christian and atheist. (Actually, Pascal only analyzed the Christian case, but the atheist case is the logical extension.) For the sake of argument, imagine for the moment that there's a 50-50 chance that God exists. (Pascal assumed that it would be the Christian God, of course.) Now, choosing the Christian envelope is equivalent to choosing to be a devout Christian. If you happen to choose this path, there are two possibilities. If you are a faithful Christian and there is no God, you just fade into nothingness when you die. But if there is a God, you go to heaven and live for eternity in bliss: infinity. So the expected value of being a Christian is:
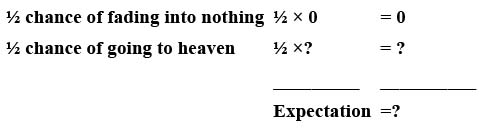
After all, half of infinity is still infinity. Thus, the value of being a Christian is infinite. Now what happens if you are an atheist? If you are correctâthere is no Godâyou gain nothing from being right. After all, if there is no God, there is no heaven. But if you are wrong and there is a God, you go to hell for an eternity: negative infinity. So the expected value of being an atheist is:
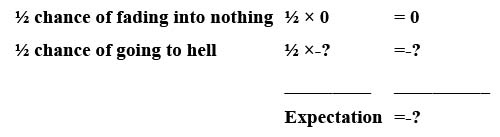
Negative infinity. The value is as bad as you can possibly get. The wise person would clearly choose Christianity instead of atheism.
But we made an assumption hereâthat there is a 50-50 chance that God exists. What happens if there is only a 1/1000 chance? The value of being a Christian would be:

It's still the same: infinite, and the value of being an atheist is still negative infinity. It's still much better to be a Christian. If the probability is 1/10,000 or 1/1,000,000 or one in a gazillion, it comes out the same. The only exception is zero.
If there is no chance that God exists, Pascal's wagerâas it came to be knownâmakes no sense. The expected value of being a Christian would then be 0 Ã?, and that was gibberish. Nobody was willing to say that there was zero chance that God exists. No matter what your outlook, it is always better to believe in God, thanks to the magic of zero and infinity. Certainly Pascal knew which way to wager, even though he gave up mathematics to win his bet.