Zero (11 page)
Authors: Charles Seife

Zero's Triumph
â¦a profound and important idea which appears so simple to us now that we ignore its true merit. But its very simplicity and the great ease which it lent to all computations put our arithmetic in the first rank of useful inventions.
âP
IERRE-
S
IMON
L
APLACE
Christianity initially rejected zero, but trade would soon demand it. The man who reintroduced zero to the West was Leonardo of Pisa. The son of an Italian trader, he traveled to northern Africa. There the young manâbetter known as Fibonacciâlearned mathematics from the Muslims and soon became a good mathematician in his own right.
Fibonacci is best remembered for a silly little problem he posed in his book,
Liber Abaci,
which was published in 1202. Imagine that a farmer has a pair of baby rabbits. Babies take two months to reach maturity, and from then on they produce another pair of rabbits at the beginning of every month. As these rabbits mature and reproduce, and those rabbits mature and reproduce, and so on, how many pairs of rabbits do you have during any given month?
Well, during the first month, you have one pair of rabbits, and since they haven't matured, they can't reproduce.
During the second month you still have only one pair.
But at the beginning of the third month, the first pair reproduces: you've got two pairs.
At the beginning of the fourth month, the first pair reproduces again, but the second pair is not mature enough: three pairs.
The next month the first pair reproduces, the second pair reproduces, since it has reached maturity, but the third pair is too young. That is two additional pairs of rabbits: five in all.
The number of rabbits goes as follows: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,â¦; the number of rabbits you have in any given month is the sum of the rabbits that you had in each of the two previous months. Mathematicians instantly realized the importance of this series. Take any term and divide it by its previous term. For instance,
8
/
5
= 1.6;
13
/
8
= 1.625;
21
/
13
=1.61538â¦. These ratios approach a particularly interesting number: the golden ratio, which is 1.61803â¦.
Pythagoras had noticed that nature seemed to be governed by the golden ratio. Fibonacci discovered the sequence that is responsible. The size of the chambers of the nautilus and the number of clockwise grooves to counterclockwise grooves in the pineapple are governed by this sequence. This is why their ratios approach the golden ratio.
Though this sequence is the source of Fibonacci's fame, Fibonacci's
Liber Abaci
had a much more important purpose than animal husbandry. Fibonacci had learned his mathematics from the Muslims, so he knew about Arabic numerals, including zero. He included the new system in
Liber Abaci,
finally introducing Europe to zero. The book showed how useful Arabic numerals were for doing complex calculations, and the Italian merchants and bankers quickly seized upon the new system, zero included.
Before Arabic numerals came around, money counters had to make do with an abacus or a counting board. The Germans called the counting board a
Rechenbank,
which is why we call moneylenders
banks.
At that time, banking methods were primitive. Not only did they use counting boards, they used
tally sticks
to record loans: a money value was written along the stick's side, and it was split in two (Figure 16). The lender kept the biggest piece, the
stock.
After all, he was the stockholder.
*
Figure 16: A tally stick
Italian merchants loved the Arabic numbers. They allowed the bankers to get rid of their counting boards. However, while businessmen saw their usefulness, the local governments hated them. In 1299, Florence banned Arabic numerals. The ostensible reason was that the numbers were easily changed and falsified. (A 0 could be turned into a 6 with a simple flourish of a pen, for instance.) But the advantages of zero and the other Arabic numerals were not so easily dispensed with; Italian merchants continued to use them, and even used them to send encrypted messagesâwhich is how the word
cipher
came to mean “secret code.”
In the end the governments had to relent in the face of commercial pressure. The Arabic notation was allowed into Italy and soon spread throughout Europe. Zero had arrivedâas had the void. The Aristotelian wall was crumbling, thanks to the influence of the Muslims and the Hindus, and by the 1400s even the staunchest European supporters of Aristotelianism had their doubts. Thomas Bradwardine, who was to become archbishop of Canterbury, tried to disprove atomism, Aristotle's old nemesis. At the same time, he wondered whether his own logic was faulty, since he based his arguments on geometry, whose infinitely divisible lines automatically reject atomism. However, the battle against Aristotle was far from over. If Aristotle were to fall, the proof of Godâa bulwark of the churchâwas no longer valid. A new proof was needed.
Worse yet, if the universe were infinite, then there could be no center. How could Earth, then, be the center of the universe? The answer was found in zero.
4
The Infinite God of Nothing
[ THE THEOLOGY OF ZERO ]
And new philosophy calls all in doubt,
The element of fire is quite put out;
The sun is lost, and th' earth, and no man's wit
Can well direct him where to look for itâ¦.'
Tis all in pieces, all coherence gone;
All just supply, and all relation:
Prince, subject, Father, Son, are things forgot.
âJ
OHN
D
ONNE
, “A
N
A
NATOMY OF THE
W
ORLD
”
Z
ero and infinity were at the very center of the Renaissance. As Europe slowly awakened from the Dark Ages, the void and the infiniteânothing and everythingâwould destroy the Aristotelian foundation of the church and open the way to the scientific revolution.
At first the papacy was blind to the danger. High-ranking clergymen experimented with the dangerous ideas of the void and the infinite, even though the ideas struck at the core of the ancient Greek philosophy that the church cherished so much. Zero appeared in the middle of every Renaissance painting, and a cardinal declared that the universe was infiniteâboundless. However, the brief love affair with zero and infinity was not to last.
When the church was threatened, it retreated into its old philosophy, turning back toward the Aristotelian doctrine that had supported it for so many years. It was too late. Zero had taken hold in the West, and despite the papacy's objections, it was too strong to be exiled once more. Aristotle fell to the infinite and to the void, and so did the proof of God's existence.
Only one option remained for the church: accept zero and infinity. Indeed, to the devout, God could be found, hidden within the void and the infinite.
The Nutshell Cracked
O God, I could be bounded in a nutshell and count myself a king of infinite space, were it not that I have bad dreams.
âW
ILLIAM
S
HAKESPEARE
,
H
AMLET
At the beginning of the Renaissance, it was not obvious that zero would pose a threat to the church. It was an artistic tool, an infinite nothing that ushered in the great Renaissance in the visual arts.
Before the fifteenth century, paintings and drawings were largely flat and lifeless. The images in them were distorted and two-dimensional; gigantic, flat knights peered out of tiny, misshapen castles (Figure 17). Even the best artists could not draw a realistic scene. They did not know how to use the power of zero.

Figure 17: Flat knights and misshapen castles
It was an Italian architect, Filippo Brunelleschi, who first demonstrated the power of an infinite zero: he created a realistic painting by using a vanishing point.
By definition, a point is a zeroâthanks to the concept of dimension. In everyday life you deal with three-dimensional objects. (Actually, Einstein revealed that our world is four-dimensional, as we shall see in a later chapter.) The clock on your dresser, the cup of coffee you drink in the morning, the book you're reading right nowâall these are three-dimensional objects. Now imagine that a giant hand comes down and squashes the book flat. Instead of being a three-dimensional object, the book is now a flat, floppy rectangle. It has lost a dimension; it has length and width, but no height. It is now two-dimensional. Now imagine that the book, turned sideways, is crushed once again by the giant hand. The book is no longer a rectangle. It is a line. Again, it has lost a dimension; it has neither height nor width, but it has length. It is a one-dimensional object. You can take away even this single dimension. Squashed along its length, the line becomes a point, an infinitesimal nothing with no length, no width, and no height. A point is a zero-dimensional object.
In 1425, Brunelleschi placed just such a point in the center of a drawing of a famous Florentine building, the Baptistery. This zero-dimensional object, the vanishing point, is an infinitesimal dot on the canvas that represents a spot infinitely far away from the viewer (Figure 18). As objects recede into the distance in the painting, they get closer and closer to the vanishing point, getting more compressed as they get farther away from the viewer. Everything sufficiently distantâpeople, trees, buildingsâis squashed into a zero-dimensional point and disappears. The zero in the center of the painting contains an infinity of space.
This apparently contradictory object turned Brunelleschi's drawing, almost magically, into such a good likeness of the three-dimensional Baptistery building that it was indistinguishable from the real thing. Indeed, when Brunelleschi used a mirror to compare the painting and the building, the reflected image matched the building's geometry exactly. The vanishing point turned a two-dimensional drawing into a perfect simulation of a three-dimensional building.

Figure 18: The vanishing point
It is no coincidence that zero and infinity are linked in the vanishing point. Just as multiplying by zero causes the number line to collapse into a point, the vanishing point has caused most of the universe to sit in a tiny dot. This is a
singularity,
a concept that became very important later in the history of scienceâbut at this early stage, mathematicians knew little more than the artists about the properties of zero. In fact, in the fifteenth century, artists were amateur mathematicians. Leonardo da Vinci wrote a guide to drawing in perspective. Another of his books, about painting, warns, “Let no one who is not a mathematician read my works.” These mathematician-artists perfected the technique of perspective and could soon depict arbitrary objects in three dimensions. No longer would artists be restricted to flat likenesses. Zero had transformed the art world.
Zero was, quite literally, at the center of Brunelleschi's painting. The church, too, dabbled with zero and the infinite, though church doctrine was still dependent on Aristotelian ideas. A contemporary of Brunelleschi, a German cardinal named Nicholas of Cusa, looked at infinity and promptly declared, “Terra non est centra mundi”: the earth is not the center of the universe. The church didn't yet realize how dangerous, how revolutionary, that idea was.
One of the old declarations of the medieval Aristotelian doctrineâas strong as the ban on the vacuumâwas the statement that Earth was unique. It was at the universe's very center. Earth's special position at the center of the universe made it the only world capable of containing life, as Aristotle held that all objects sought out their proper place. Heavy objects, like rocks or people, belonged on the ground; light objects, like air, belonged in the heavens. Not only did this imply that the planetsâin the heavensâwere made of light, airy stuff, but it also meant that any people in the heavens would naturally fall to Earth. Thus creatures could only inhabit the nutmeat in the center of the nutshell cosmos. Having other planets with life on them was as silly as having a sphere with two centers.
When Tempier declared that the omnipotent God could create a vacuum if he so desired, Tempier insisted that God could break any Aristotelian law. God could create life on other worlds if he wished. There could be thousands of other Earths, each teeming with creatures; it was certainly within God's power, whether Aristotle agrees or not.
Nicholas of Cusa was bold enough to say that God
must
have done so. “The regions of the other stars are similar to this,” he said, “for we believe that none of them is deprived of inhabitants.” The sky was littered with an infinite number of stars. The planets glowed in the heavens; the moon and the sun each glowed with light. Why couldn't the stars in the sky be planets or moons or suns on their own? Maybe Earth glows brightly in their heavens, just as they glow in ours. Nicholas was sure that God had, indeed, created an infinite number of other worlds. Earth was no longer at the center of the universe. Yet Nicholas was not declared a heretic, and the church didn't react to the new idea.
In the meantime another Nicholas turned Cusa's philosophy into a scientific theory. Nicolaus Copernicus showed that Earth is not the center of the universe. It revolves around the sun.
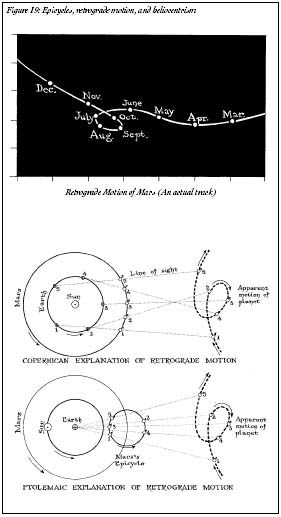
A Polish monk and a physician, Copernicus learned mathematics so he could cast astrological tables, the better to cure his patients with. Along the way, Copernicus's dabblings with the planets and stars showed him how complicated the old Greek system of tracking the planets was. Ptolemy's clockwork heavensâwith Earth at the centerâwere extremely accurate. However, they were terribly complex. Planets course around the sky throughout the year, but every so often they stop, move backward, and then shoot ahead once more. To account for the planets' bizarre behavior, Ptolemy added
epicycles
to his planetary clockwork: little circles within circles could explain the backward, or
retrograde
, motion of the planets (Figure 19).
The power of Copernicus's idea was in its simplicity. Instead of placing Earth at the center of the universe filled with epicycle-filled clockworks, Copernicus imagined that the sun was at the center instead, and the planets moved in simple circles. Planets would seem to zoom backward as Earth overtook them; no epicycles were needed. Though Copernicus's system didn't agree with the data completelyâthe circular orbits were wrong, though the heliocentric idea was correctâit was much simpler than the Ptolemaic system. The earth revolved around the sun.
Terra non est centra mundi.
Nicholas of Cusa and Nicolaus Copernicus cracked open the nutshell universe of Aristotle and Ptolemy. No longer was the earth comfortably ensconced in the center of the universe; there was no shell containing the cosmos. The universe went on into infinity, dotted with innumerable worlds, each inhabited by mysterious creatures. But how could Rome claim to be the seat of the one true Church if its authority could not extend to other solar systems? Were there other popes on other planets? It was a grim prospect for the Catholic Church, especially since it was beginning to have trouble with its subjects on even its own world.
Copernicus published his magnum opus on his deathbedâin 1543, just before the church started clamping down on new ideas. Copernicus's book,
De Revolutionibus,
was even dedicated to Pope Paul III. However, the church was under attack. As a result, the new ideasâthe questioning of Aristotleâcould no longer be tolerated.
The attack on the church began in earnest in 1517, when a constipated German monk nailed a list of complaints to the door of the church in Wittenberg. (Luther's constipation was legendary. Some scholars believe that his great revelation about faith came to him when he was sitting on the privy. “Luther's release from the constricting bondage of fear corresponded to the release of his bowels,” notes one text, commenting on this theory.) This was the beginning of the Reformation; intellectuals everywhere began to reject the authority of the pope. By the 1530s, in a quest to ensure an orderly succession to the throne, Henry VIII had spurned the authority of the pope, declaring himself the head of the English clergy.