Understanding Sabermetrics (25 page)
Read Understanding Sabermetrics Online
Authors: Gabriel B. Costa,Michael R. Huber,John T. Saccoma
4.
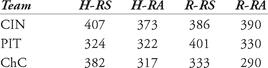
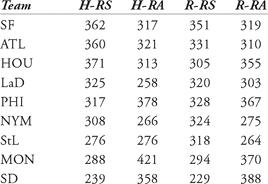
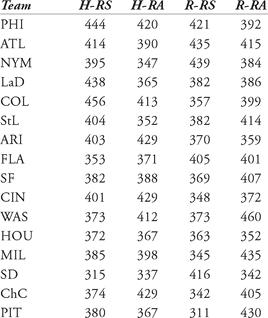
a. Calculate the PF for each NL team in 1969. Classify each as “Pitcher’s,” “Hitter’s,” or “Neutral.”
b. Repeat the directions for part (a) for the NL in 2006.
5.
a. The ballpark in Oakland had a PF of 0.92 in 2006. It is historically a pitchers’ park. Calculate the RC number for Nick Swisher using HDG-23.
b. Calculate Swisher’s RC/27, and adjust it for home park.
1.
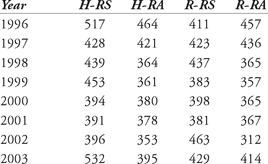
a. Calculate the PF for Fenway Park for each season from 1996 to 2003. Use the table below, and note that the Red Sox played 81 home games and only 80 road games in 2001. Are there any obvious anomalies?
b. Calculate PF-3 and PF-5 for each season where appropriate (see Baltimore calculations earlier in the chapter for guidance).
c. Using HDG-23, calculate Manny Ramirez’s Runs Created for the 2003 season.
d. Adjust Ramirez’s RC total using PF, PF-3, and PF-5, as calculated in part (b) .
e. Calculate Manny’s RC/27, and correct for home park.
f. Were Manny Ramirez’s runs created and RC/27 totals helped or hindered by Fenway Park? Justify your answer.
Inning 9: Creating Measures and Doing Sabermetrics — Some Examples
In their classic book
The Hidden Game of Baseball
, John Thorn and Pete Palmer write: “Baseball may be loved without statistics, but it cannot be understood without them.” It seems that pretty much everyone associated with the game — from Henry Chadwick, who derived a “total bases per game” statistic circa 1860, to the present — agrees with Thorn and Palmer. Indeed the very purpose of this book is an attempt to better explain the game of baseball by using statistics.
The Hidden Game of Baseball
, John Thorn and Pete Palmer write: “Baseball may be loved without statistics, but it cannot be understood without them.” It seems that pretty much everyone associated with the game — from Henry Chadwick, who derived a “total bases per game” statistic circa 1860, to the present — agrees with Thorn and Palmer. Indeed the very purpose of this book is an attempt to better explain the game of baseball by using statistics.
In this book we have referred to Thorn and Palmer (and their linear weights), and others, such as Bill James (runs created), who have created well-known measures and instruments. As we have seen, each measure has certain properties and nuances.
There is an art to creating a measure: it should be fairly easy to understand and not too difficult to compute. For example, to compute a batting average (BA), one merely divides the total number of hits by the total number of at-bats
.
Rounded off to the nearest thousandth, it is not only easily computed but is also easily understood. The constituent
ingredients
of hits and at-bats are very easy to obtain from the sports section of newspapers, from baseball books, and from the Internet.
.
Rounded off to the nearest thousandth, it is not only easily computed but is also easily understood. The constituent
ingredients
of hits and at-bats are very easy to obtain from the sports section of newspapers, from baseball books, and from the Internet.
Continuing with this example, we see that the extremes range from .000 (no hits) to 1.000 (a hit every time one bats). Another property of this model is that
extra base hits
are weighted the same as singles. Also, this statistic gives no information about either runs batted in or runs scored
.
Nor does it reveal anything about streaks, clutch hitting (however we wish to define these two ideas), day vs. night performances, etc.
extra base hits
are weighted the same as singles. Also, this statistic gives no information about either runs batted in or runs scored
.
Nor does it reveal anything about streaks, clutch hitting (however we wish to define these two ideas), day vs. night performances, etc.
One way of dealing with some of the shortcomings of BA, is to use split statistics
.
Nowadays these numbers are easily found on the Web. Here, we can discover how well or poorly a batter does regarding such factors as: day vs. night, righty vs. lefty, natural grass vs. artificial turf, etc.
.
Nowadays these numbers are easily found on the Web. Here, we can discover how well or poorly a batter does regarding such factors as: day vs. night, righty vs. lefty, natural grass vs. artificial turf, etc.
Batting averages can sometimes assist us in attempts to span eras. Players like Ty Cobb and Rogers Hornsby more than once batted over .400, yet no once since Ted Williams in 1941 has repeated this feat. And in 1968, Carl Yastrzemski led the American League with a mark of .301. Can these numbers be compared in any reasonable way?
One approach is to compare a player with his peers. For example, let us compare two batting champions. In 1911, Ty Cobb hit .420 while the league averaged .273; in 1968, the year Yastrzemski batted .301, the American league batted .230. If we divide Cobb’s average by the league’s mark we get a ratio of 1,538; repeating the process for Yastrzemski gives us 1.309. What do these numbers mean?
We can think of these ratios as normalization factors which may give us a sense of how these Hall of Famers performed relative to their peers. In other words, while there was a difference of 119 percentage points between the Georgia Peach and Yaz with respect to BA, we can think of Cobb as being 1.538 times as good as the 1911 average hitter in the American League, while his counterpart was 1.309 times as good as his peers.
It would seem that this approach does indeed shed new light on the “search for objective knowledge” about baseball. In particular, this methodology can assist us in leveling the playing fields when comparing players of different times. Bottom line: at times, ratios are more revealing than differences.
One final comment: there are many statistics which deal with hitting and quite a few which evaluate pitching. Because fielding is much more difficult to “measure,” there are relatively few instruments dealing with this aspect of the game.
Here are some questions toward a methodology to assist in creating sabermetrical measures:
• What do I want the model to demonstrate?
• Does this instrument reveal something heretofore unknown?
• Does the model lend itself to clear interpretations?
• Can I easily obtain the constituent factors necessary for the model?
• Is the measure too difficult to compute, thereby rendering it virtually useless?
• Are there extreme cases? If so, what happens to the measure in these cases?
• What are the shortcomings of the instrument?
• Can I use the model for different eras?
• Do results from this model seem to agree with findings from the use of similar models?
Let’s compare apples and oranges. Ty Cobb won 12 batting titles in 13 years (1907 through 1919, excepting 1916) while Babe Ruth gathered 13 slugging titles in 14 years (1918 through 1931, save 1925). It would be difficult to find two more dominant streaks in baseball history. Is there any instrument we can use to compare these two sustained performances?
As we know, batting averages range from .000 to 1.000, while slugging percentages can vary from .000 to 4.000. So differences between champions is not a realistic measure. For example, Cobb outhit the American League runner-up by 12 points in 1911 (.420 to .408) while Ruth outslugged his nearest rival by 215 points in 1920 (.847 to .632).
The league batting average in 1911 was .273; dividing this into Cobb’s .420 mark gives a ratio of 1.538. We could interpret this as saying that Cobb was better that one and a half times the average league hitter in 1911. That’s pretty impressive.
In 1920, the American League slugged .387. When this average is divided into Ruth’s .847, we see arrive at a ratio of 2.189, perhaps interpreting this as saying that Ruth was better than twice the average slugger in 1920.
What does this mean? We’re not sure; but when one “does the math” we find that Ruth’s lowest ratio of the 13 years he won the title occurred in 1922, when he slugged .672, the league slugged .398, thus giving a ratio of 1.688. Cobb’s
highest
ratio of 1.584 was compiled in 1910 when the league batted .243 and the Georgia Peach hit .385.
highest
ratio of 1.584 was compiled in 1910 when the league batted .243 and the Georgia Peach hit .385.
Other books
Sacrifice by Sharon Bolton
A Small Weeping by Alex Gray
Revolution (The Revelation Series Book 4) by Randi Cooley Wilson
Zoey And The Nice Guy (Big Girl Panties #1) by Carter Ashby
Fingerless Gloves by Nick Orsini
Indian Country Noir (Akashic Noir) by Sarah Cortez;Liz Martinez
The Massacre Mechanism (The Downwinders Book 5) by Michael Richan
After the Fall by Patricia Gussin
Hello Loved Ones by Tammy Letherer
Fallen by Karin Slaughter