Coming of Age in the Milky Way (18 page)
Read Coming of Age in the Milky Way Online
Authors: Timothy Ferris
Tags: #Science, #Philosophy, #Space and time, #Cosmology, #Science - History, #Astronomy, #Metaphysics, #History

A P
LUMB
L
INE TO THE
S
UN
In Tahiti … the women are possessed of a delicate organization, a sprightly turn of mind, a lively, fanciful imagination, a wonderful quickness of parts and sensibility, a sweetness of temper, and a desire to please.
—Johann Georg Forster, 1778
T
he conception of the solar system that the Western world had attained by the beginning of the eighteenth century was accurate in its proportions but indeterminate in scale. Thanks principally to the theoretical work of Copernicus and Kepler and to the observations of Tycho and Galileo, it had been established beyond dispute that the earth was one of five known planets moving in elliptical orbits around the sun. And, thanks to Newton, these motions could be interpreted and predicted in terms of a mathematically cogent dynamical scheme that embraced terrestrial as well as extraterrestrial physics. But, though the relative distances of the sun and planets were understood, their absolute distances were not.
Copernicus had measured the proportions of the solar system to within 5 percent of the correct values, and Kepler had come closer still. These relative distances customarily were expressed in terms of the distance from the earth to the sun, a quantity known as the astronomical unit. But nobody knew what the distance to
the sun might be; in other words, the value of the astronomical unit had not been determined. Here was a clear challenge. Since the proportions of the system already were known, if the distance to the sun or to any one planet could be ascertained, the distances of all the other planets would follow. And, since the apparent diameters of the planets could by now be measured rather well, by using a micrometer eyepiece attached to a good telescope, the sizes of the planets could be ascertained as soon as their distances had been measured. Beyond that lay the exciting prospect that, by using the astronomical unit as a baseline, it might be possible to triangulate nearby stars and measure their distances as well. Accomplishing this feat constituted one of the heroic endeavors of eighteenth-century astronomy.
Traditional estimates of the distance from the earth to the sun were of little help. Beginning with Hipparchus in the second century
B.C.
and ranging down through Ptolemy, Copernicus, and Tycho, astronomers had assumed as a rule of thumb that the astronomical unit was equal to about twelve hundred times the radius of the earth—in modern figures, some 4.8 million miles. Such a distance seemed appropriately vast; to borrow a conceit from the thirteenth century, had Adam started walking on the day of the creation (usually set at 4004
B.C.
) he would have required six hundred years to reach the sun, and would have arrived, footsore, at the planet Jupiter in the twentieth century. Nevertheless, an astronomical unit of twelve hundred earth radii was twenty times smaller
than the real distance. Kepler and later observers suspected that it was an underestimate—Kepler guessed that the value was more like thirty-five hundred earth radii, nearly three times the previous estimates—but these early observers lacked observational instruments adequate to test their hunches.
Two ways of obtaining distance data were available. One, micrometry, was theoretically crude but practically accessible. The other, triangulation, was perfect in theory but difficult to accomplish in practice.
Micrometry consisted of using a micrometer—an eyepiece equipped with an adjustable knife blade—to measure the apparent diameter of a planet as seen through a telescope. The astronomer then estimated the distance of a planet by comparing its apparent diameter with what he guessed to be its actual diameter. Obviously, the result could be no better than the guess as to the planet’s diameter. A few astronomers guessed very well indeed: Christian Huygens in 1659 assumed that the diameter of Mars was about 60 percent that of the earth (the correct figure is 53 percent), then measured the apparent size of the disk of Mars through a telescope and calculated a value for the astronomical unit of one hundred million miles. This came astonishingly close to the truth—the mean distance separating the earth from the sun is ninety-three million miles—but it depended entirely upon the accuracy of Huygens’s hunch about the size of Mars, and that, as Huygens himself was the first to concede, was “a slippery basis” upon which to base so important a result.
1
The issue was not who made the luckiest guess, but who could obtain observational data that would establish the value of the astronomical unit to everyone’s satisfaction. This micrometry alone could not do.
Triangulation, called parallax (from the Greek
parallaxis
, for the value of an angle), was the sounder method. If a planet were observed simultaneously by two observers stationed thousands of miles apart—one in France, say, and the other in Mexico—its position against the background stars would appear to be slightly altered for the astronomer in Mexico as compared to the one in France, owing to their different perspectives on it. If both this angle and the baseline distance separating the two astronomers could be measured, the distance to the planet could be calculated through the straightforward application of euclidean geometry.
That triangulation was theoretically sound had been appreciated
since ancient times. The difficulty lay in execution. First, one had to know the exact distance between two widely separated observers; this required reasonably accurate intercontinental maps. Second, the observations had to be carried out at the same time, to avoid errors introduced by the motions of the planets and by the rotation of the earth on its axis; this required accurate clocks and a way of synchronizing them. Third, the position of the planet against the stars had to be plotted precisely, because any triangle drawn between a planet and two points on Earth is going to be a very long, thin triangle indeed. Still, the thing could be done, given sufficient exactitude in the measurement of terrestrial space and time.
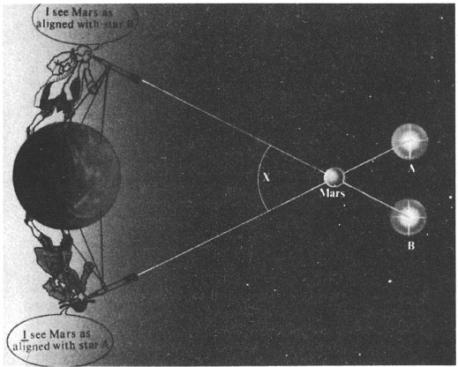
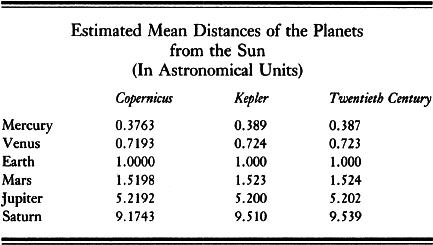
The parallax of Mars was first obtained by simultaneously observing the planet’s apparent location from two widely separated places on Earth. The difference in perspective made it possible to measure the value of angle
X
, which yields the distance from Earth to Mars. The angle, however, is small: Were the earth the size depicted in this illustration, Mars would be five hundred feet away.
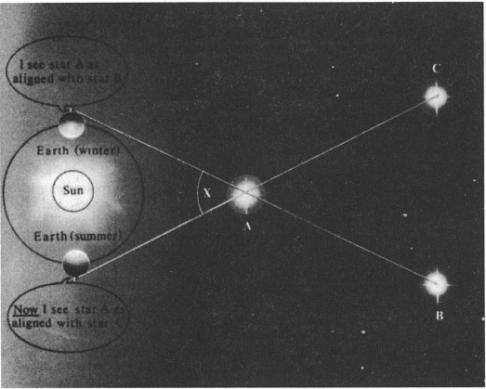
The parallax of stars can best be measured by using as a baseline not the earth but the earth’s orbit around the sun. Even with so large a baseline, however, angle
X
is
extremely
small: Were the earth’s orbit the size here depicted, the nearest star would be more than two miles away.
Fortunately for science, rapid progress was being made in both cartography and chronometry. The agency responsible, however, was less the pursuit of pure knowledge than the accumulation of the booty of empire. The wealth of the world flowed into eighteenth-century Europe in ships: From their holds came the Indian rosewood of the dining tables where Newton and Halley were entertained, the African gold inlay on the plates, the turkey with corn they were served as the main course, the chocolate for dessert, and the tobacco they smoked afterward. But blue-water navigation was as hazardous as it was inexact, and sailors who ventured far beyond the sight of land were forever groping their way in the unknown—they were “at sea,” as we still say today—with results
that ranged from delay to disaster. Many a cargo of silver, sugar, or hardwood had been conveyed across the Atlantic or Indian oceans only to be dashed against the rocks of Land’s End or the Cape of Good Hope. The situation had improved little in the century that had passed since the geographer Richard Hakluyt wrote of navigators that “no kind of men in any profession in the commonwealth pass their years in so great and continual hazard of life. … Of so many, so few grow to gray hairs.”
2
The definitive catastrophe came in 1707, when Sir Cloudesley Shovell, four ships of his fleet, and fully two thousand of his men were lost on the rocks of the Scilly Islands of southwest England, this on a night when his navigators had reckoned that the fleet was in safe waters hundreds of miles to the west. Clearly, something had to be done.
The problem had to do with the determination of longitude. It had long been possible for a ship’s navigator to find his latitude—his location in a north-south direction—by measuring the altitude above the horizon of the pole star or of the sun at noon. The instrument employed for this purpose was the astrolabe (from the Greek for “to take a star”), a disk made of copper or tin, five to seven inches in diameter, fitted with a movable sighting arm. At local noon on any clear day aboard a ship of the line, three officers could be seen helping to shoot the sun—one holding the astrolabe steady, another sighting it, and a third reading the elevation—while deckhands stood by to catch the navigator when he fell or to retrieve the astrolabe if it were dropped and went scuttling across the rolling deck. The efficiency of the astrolabe had been improving, through the endeavors of Newton, Halley, John Hadley, Thomas Godfrey, and others, who made the instrument less cumbersome by reducing it first to a quarter of a circle (the “quadrant”), then to a sixth (the “sextant”), by employing mirrors to fold its optics so that the observer could see sun and horizon superimposed, and by adding filters and a telescope for greater accuracy. But, although these improvements helped navigators refine their calculations of latitude, they did not help them determine their longitude—their position in the east-west direction. Here the question was as much one of time as of space.
As the earth turns, the stars troop across the sky at a rate of fifteen degrees per hour. This means that if you know the time, the sky will tell you where you are. But knowledge of the exact
time was just what navigators of Newton’s day lacked. On land, time was kept by pendulum clocks, but pendulums do not work at sea; the rolling of the boat wrecks their performance. A typical ship’s clock in the early eighteenth century was accurate to no better than five or ten minutes per day, which translated into a miscalculation of fully five hundred miles in longitude after only ten days at sea. It was just such an error that had dashed Cloudesley Shovell’s fleet on the rocks of the Scilly Islands.
The problem of determining longitude at sea had defied resolution for so long that many regarded it as unsolvable. The mathematician in Cervantes’s
The Dog’s Dialog
muses crazily that he has “spent twenty-two years searching for the fixed point”—
el punto fijo
, the correct longitude—“and here it leaves me, and there I have it, and when it seems I really have it and it cannot possibly escape me, then, when I am not looking, I find myself so far away again that I am astonished. The same thing happens with squaring the circle.”
3
Sebastian Cabot on his deathbed claimed that God had revealed the answer to him, but added, alas, that He had also sworn him to secrecy.