Coming of Age in the Milky Way (16 page)

As the years passed, Newton elaborated the calculus, advanced the art of analytical geometry, did pioneering work in optics, and conducted innumerable experiments in alchemy (possibly poisoning himself in the process; some of the symptoms of a mental breakdown he suffered in 1693 are consistent with those of acute mercury toxemia). All this he did in silence. Occasionally he reported on his research in his lectures, but few of the professors and fewer among the students could follow his train of thought, and so few came. Sometimes nobody at all showed up, whereupon Newton, confronted with the empty hall, would trudge back to his rooms, evidently unperturbed.

The outer world eventually intruded nonetheless. In the case of Newton, who shunned notoriety, as in that of Galileo, who welcomed it, the agency responsible was the telescope.

Newton was handy, and liked to build experimental devices. (A good thing, said a colleague, for he took no exercise and had no hobbies and would otherwise have killed himself with overwork.) He wanted a telescope with which to observe comets and the planets. The only type of telescope in use at the time was the refractor—the sort that Galileo built, with a large lens at the front end to gather light. Newton disliked refractors; his extensive studies of optics had acquainted him with their tendency to introduce spurious colors. To overcome this defect he invented a new kind of telescope, one that employed a mirror rather than a lens to collect light.
Efficient, effective, and cheap, the “Newtonian reflector” was to become the most popular telescope in the world. It brought Newton’s name to the attention of the Royal Society of London, which elected him to membership and prevailed upon him to publish a short paper he had written on colors. This decision he soon regretted; the paper drew twelve letters, prompting Newton to complain to Henry Oldenburg, the society’s secretary, that he had “sacrificed my peace, a matter of real substance.”
⁹

The Royal Society was the most influential of the several scientific societies that had sprung up in the seventeenth century, each devoted to the empirical study of nature without interference by Church or State. The first of these, the Italian Academy of the Lynx, was founded in 1603 and had formed a platform from which Galileo, its most famous member, conducted his polemics. Founded under the amateur physicist King Charles II, the Royal Society
was too poor to afford a laboratory or even an adequate headquarters, but was fiercely independent and proudly unfettered by tradition or superstition. Its temper had been expressed by Oldenburg in a letter to the philosopher Benedict Spinoza:

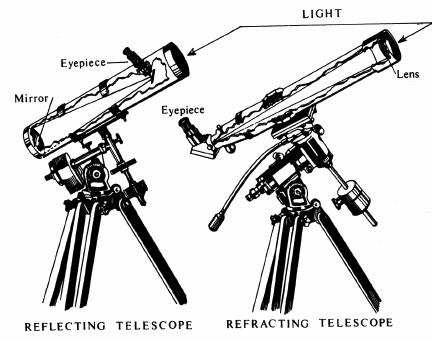
Reflecting telescopes gather light by means of a curved mirror, refracting telescopes by a curved lens.

This clear new cast of mind was personified by the three members of the Royal Society—Edmond Halley, Christopher Wren, and Robert Hooke—who lunched together in a London tavern one cold January afternoon in 1684. Wren, who had been president of the Royal Society, was an astronomer, geometer, and physicist, and the architect of St. Paul’s Cathedral—where his body is entombed, with an epitaph composed by his son inscribed on the cathedral wall that reads,
IF YOU SEEK A MONUMENT, LOOK AROUND.
Hooke was an established physicist and astronomer, the discoverer of the rotation of Jupiter; it was he who had worded the society’s credo: “To improve the knowledge of natural things, and all useful Arts, Manufactures, Mechanic practices, Engines and Inventions by Experiments (not meddling with Divinity, Metaphysics, Morals, Politics, Grammar, Rhetoric or Logic).”
¹¹
Halley at twenty-seven years old was a generation younger than his two companions, but he had already made a name for himself in astronomy, charting the southern skies from the island of St. Helena in the South Atlantic and there conducting pendulum experiments that showed a deviation in gravitational force caused by the centrifugal force of the earth’s rotation. Ahead lay a distinguished career highlighted by Halley’s compiling of actuarial tables, drawing maps of magnetic compass deviations and a meteorological map of the earth, and identifying as periodic the comet that has since borne his name.

Over lunch, Halley and Hooke discussed their shared conviction that the force of gravitation must diminish by the square of the distance across which it is propagated. They felt certain that the inverse-square law could explain Kepler’s discovery that the
planets move in elliptical orbits, each sweeping out an equal area within its orbit in an equal time. The trouble was, as Halley noted, that he could not demonstrate the connection mathematically. (Part of the problem was that nobody, except the silent Newton, had realized that the earth’s gravitational force could be treated as if it were concentrated at a point at the center of the earth.) Hooke brashly asserted that he had found the proof, but preferred to keep it a secret so that others might try and fail and thus appreciate how hard it had been to arrive at it. Perhaps he meant to echo Descartes’s
Geometry
, which ends with the infuriating declaration that the author has “intentionally omitted” elements of his proofs “so as to leave to others the pleasure of discovery.”
¹²
In any event, Wren had his doubts about Hooke’s mathematical ability if not Descartes’, and he offered as a prize to Hooke or Halley a book worth up to forty shillings—an expensive book—if either could produce such a demonstration within two months. Hooke immediately agreed, but the two months passed and he failed to come up with the proof. Halley tried, and failed, but kept thinking about the matter.

The man who might be able to answer it, he realized, was Newton. Newton was forbidding, to be sure; his amanuensis, Humphrey Newton (no relation), said he had seen his master laugh only once in five years, this when Newton inquired of an acquaintance what he thought of a copy of Euclid he had loaned him, and the man asked what use or benefit its study might be in his life, “upon which Sir Isaac was very merry.”
¹³
But when the two men had met a couple of years earlier, Newton pumping Halley for data on the great comet of 1680, they had got along reasonably well. So, in August, while visiting Cambridge, Halley stopped in to see Newton again.

What, Halley asked Newton, would be the shape of the orbits of the planets if the gravitational force holding them in proximity to the sun decreased by the square of their distance from the sun?

An ellipse, Newton answered without hesitation.

Halley, in a state of “joy and amazement” as Newton recalled the moment, asked Newton how he knew this answer to be true.

Newton replied that he had calculated it.

Halley asked if he might see the calculation.

Newton searched through some of the stacks of papers that littered his quarters. There were thousands of them. Some bore
the spiderweb tracings of his diagrams in optics. Others, adorned with medieval symbols and ornate diagrams of the philosophers’ stone, recorded his explorations of alchemy. A paper crammed with columns of notes compared twenty different versions of the Book of Revelations, part of the theological research Newton had conducted in substantiating his opposition to the doctrine of the Trinity—this a deep secret for the Lucasian Professor of Mathematics at Trinity College. Other pages were devoted to Newton’s attempts to show that the Old Testament prophets had known that the universe is centered on the sun, and that the geocentric cosmology upheld by the Roman Catholic Church was therefore a corruption. But-, Newton said, he could not find his calculations connecting the inverse-square law to Kepler’s orbits. He told Halley he would write them out anew and send them to him.

Newton had calculated elliptical orbits five years earlier, upon his return from a stay of nearly six months at his mother’s farm in Woolsthorpe, where he had gone when he learned that she had fallen mortally ill with a fever. His behavior there displayed a tenderness we do not normally associate with this frosty man: “He attended her with a true filial piety, sat up whole nights with her, gave her all her Physic himself, dressed all her blisters with his own hands, and made use of that manual dexterity for which he was so remarkable to lessen the pain which always attends the dressing,” reported John Conduitt, who wrote notes for a memoir on Newton’s life.
¹⁴
The semiliterate Hannah Newton Smith could not have understood much of what her firstborn son did and thought, but her devotion to him was unwavering. A letter she wrote him shortly before his graduation from Cambridge survives; one edge has been burned away (perhaps by Newton, who destroyed many of his papers) and a few words are missing, but what remains contains the word “love” three times in two lines:

She was buried on June 4, 1679. Conduitt described her as a woman of “extraordinary … understanding and virtue.”

When Newton returned to Cambridge after his mother’s death, he returned as well to the study of universal gravitation. He had paid little attention to the problem since the time, years before, when he had watched the apple fall outside the window of his room in his mother’s farmhouse. But now he was blessed with an antagonist—none other than Hooke himself, the tight-lipped claimant to the inverse-square law, who had written him with questions concerning the trajectory described by an object falling straight toward a gravitationally attractive body. Newton, aloof as usual, replied by declining Hooke’s invitation to correspond further, but took the trouble to answer Hooke’s questions, and in so doing made a mistake. Hooke seized upon the error, pointing it out in a letter of reply. Furious at himself, Newton concentrated on the matter for a time, and in the process verified to his own satisfaction that gravity obeying an inverse-square law could be shown to account for the orbits of the planets. Then he put his calculations aside. These were the papers he referred to when Halley came calling.

But they, too, turned out to contain an error—which may explain why the cautious Newton said he was “unable” to find them in the first place—and so Newton was obligated to resume work on the problem in order to satisfy his promise to Halley. This he did, and three months later, in November, he sent Halley a paper that successfully derived all three of Kepler’s laws from the precept of universal gravitation obeying an inverse-square law. Halley, immediately recognizing the tremendous importance of Newton’s accomplishment, hastened to Cambridge and urged him to write a book on gravitation and the dynamics of the solar system. Thus was born Sir Isaac Newton’s
Mathematical Principles of Natural Philosophy and His System of the World
—the
Principia
.

Work on the book took over Newton’s life. “Now I am upon this subject,” he wrote the astronomer John Flamsteed, in a letter soliciting data on the orbits of Saturn’s satellites, “I would gladly know the bottom of it before I publish my papers.”
¹⁶
The effort only intensified his air of preoccupation. His amanuensis Humphrey Newton observed that

Newton still wandered alone in the gardens, as he had since his undergraduate days, and when fresh gravel was laid in the walks he drew geometric diagrams in it with a stick (his colleagues carefully stepping around the diagrams so as not to disturb them). But now his walks were more often interrupted by bolts of insight that sent him running back to his desk in such haste, Humphrey Newton noted, that he would “fall to write on his Desk standing, without giving himself the Leisure to draw a Chair to sit down in.
¹⁸
”

Newton’s surviving drafts of the
Principia
support Thomas Edison’s dictum that genius is one percent inspiration and ninety-nine percent perspiration. Like Beethoven’s drafts of the opening bars of the Fifth Symphony, they are characterized less by sudden flashes of insight than by a constant, indefatigable hammering away at immediate, specific problems; when Newton was asked years later how he had discovered his laws of celestial dynamics, he replied, “By thinking of them without ceasing.”
¹⁹
Toil was transmuted into both substance and veneer, and the finished manuscript, delivered to Halley in April 1686, had the grace and easy assurance of a work of art. For the modern reader the
Principia
shares with a few other masterworks of science—Euclid’s
Elements
among them, and Darwin’s
Origin of Species
—a kind of inevitability, as if its conclusions were self-evident. But the more we put ourselves into the mind-set of a seventeenth-century reader, the more it takes on the force of revelation. Never before in the history of empirical thought had so wide a range of natural phenomena been accounted for so precisely, and with such economy.