Chances Are (11 page)
Authors: Michael Kaplan

Thus embedded, probabilityâunderstood as the mathematics of randomnessâfound again the rigor of deductive logic. True, it appeared at first to be a somewhat chilly rigorâone that its practitioners were keen to distinguish from the questionable world of applications. William Feller, who wrote the definitive mid-twentieth century textbook on probability, began it by pointing out: “We shall no more attempt to explain âthe meaning' of probability than the modern physicist dwells on the âreal meaning' of mass and energy.” Joseph Doob, one of the most prominent, if stern, proponents of probability theory, said that it was as useless to debate whether an actual sequence of coin tossing was governed by the laws of probability as “to debate the table manners of children with six arms.” As always, the counselors of perfection demand a retreat from the world.
That, though, was to reckon without humanity. Our desire to come to some conclusionâeven if it's not certaintyâmeans we are bound to take this specialist tool of probability and risk its edge on unknown materials. Kolmogorov's legacy is applied every day in science, medicine, systems engineering, decision theory, and computer simulations of the behavior of financial markets. Its power comes from its purityâits conceptual simplicity. We are no longer talking specifically about the behavior of physical objects, observations, frequencies, or opinionsâjust measures. Purged of unnecessary ritual and worldly considerations, uniting its various sects, mathematical probability appears as the one true faith.
But having a true faith is not always the end of difficulties. Consider a simple problem posed by the French mathematician Joseph Bertrand: you have a circle with a triangle drawn inside itâa triangle whose sides are equal in length.
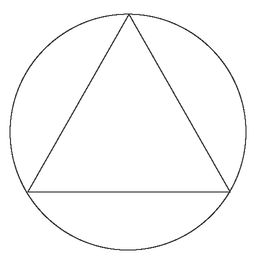
Now you draw a line at random so that it touches the circle in two places: this is called a
chord
. What is the probability that this chord is longer than a side of the triangle?
chord
. What is the probability that this chord is longer than a side of the triangle?
One good path to an answer would be this: line up a corner of our triangle with one end of the chord; we can now see that any chord that falls
within
the triangle will be longer than a side.
within
the triangle will be longer than a side.
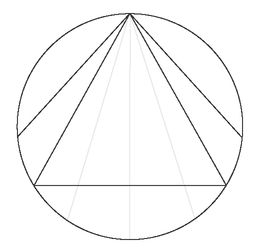
Since the starting angle of lines that cross the triangle is one-third the angle of all possible chords you could draw from that point, this suggests that the probability that a random chord will be longer than a side of the triangle is 1/3.
But here is a different approach. Let's say you take your chord and roll it across the circle like a pencil across the floor.
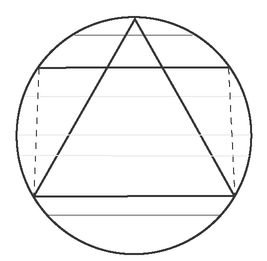
We can see that any chord falling within the rectangle built on a side of the triangle will be longer than that side. The height of that rectangle is exactly half the diameter of the circle; so the probability that a random chord will be longer than a side of the triangle is 1/2· Paradox.
Probability remains, as Charles Peirce pointed out, the only branch of mathematics “in which good writers frequently get results entirely erroneous.” Defining probability in terms of measure is clear, consistent, and intuitively satisfying; but, as Bertrand's paradox reveals, we must be very careful in how we set up our problemsâin this case, how we define that unassuming phrase “drawn at random.” Just as in the Delphic temple, the validity of the answer will depend on the nature of the question. You must be careful what you pray for.
4
Gambling
In play there are two pleasures for your choosing;
The one is winning and the otherâlosing.
The one is winning and the otherâlosing.
âByron,
Don Juan
, Canto XIV
Don Juan
, Canto XIV
Â
Â
Â
Â
Â
Â
Â
A
summer's evening in Monte Carlo. The warm breeze is scented with salt, aftershave, cigar smoke, and marine diesel. As you climb the carpeted steps, your tread silent but determined, the marble façade glows pinkly above you while golden effigies smile down. You feel lucky: chosen, fortunate, blessedâthough you might wonder idly as you pass through the glowing Salon de l'Europe why it is that these people have so many more and bigger chandeliers than you do. The answer is simple: some things happen more often than other things . . . in the long run.
summer's evening in Monte Carlo. The warm breeze is scented with salt, aftershave, cigar smoke, and marine diesel. As you climb the carpeted steps, your tread silent but determined, the marble façade glows pinkly above you while golden effigies smile down. You feel lucky: chosen, fortunate, blessedâthough you might wonder idly as you pass through the glowing Salon de l'Europe why it is that these people have so many more and bigger chandeliers than you do. The answer is simple: some things happen more often than other things . . . in the long run.
“Mesdames et messieurs, faites vos jeux.”
Roulette is a teaching machine for basic probability. Look at the wheel and the cloth, and you will see that here is a device for counting events and gathering them into separate groups. There are 36 numbered cups on the wheel, alternating red and black. Given the compounded, confusing effects of the speed of the wheel, the baffles and deflectors, the bounce of the ball, and the casual flick of the croupier's wrist, you have no intrinsic reason to believe the ball will land in one of those cups sooner than in any other: the 36 chances appear equal. Given a long enough time, then, you can expect each cup to receive the ball in 1/36 of the total number of spins.
Roulette is a teaching machine for basic probability. Look at the wheel and the cloth, and you will see that here is a device for counting events and gathering them into separate groups. There are 36 numbered cups on the wheel, alternating red and black. Given the compounded, confusing effects of the speed of the wheel, the baffles and deflectors, the bounce of the ball, and the casual flick of the croupier's wrist, you have no intrinsic reason to believe the ball will land in one of those cups sooner than in any other: the 36 chances appear equal. Given a long enough time, then, you can expect each cup to receive the ball in 1/36 of the total number of spins.
You may bet on a single number, two numbers, three, four, five (in the United States), six, twelve, or eighteen, grouped in various ways: odd or even, red or black, low or high, quadrants of the wheel or
orphelins
âleftovers after some such quadrature. The house, obligingly, adjusts the odds it offers you to the proportion of the 36 numbers represented by your bet, from 36 times (including your original stake) for a single number down to doubling your money on winning bets that split the numbers in half. Indeed, one reason the roulette wheel has 36 numbers is that 36 divides so neatly into different proportions, accommodating everyone's secret sense of fate's symmetry and neatness.
orphelins
âleftovers after some such quadrature. The house, obligingly, adjusts the odds it offers you to the proportion of the 36 numbers represented by your bet, from 36 times (including your original stake) for a single number down to doubling your money on winning bets that split the numbers in half. Indeed, one reason the roulette wheel has 36 numbers is that 36 divides so neatly into different proportions, accommodating everyone's secret sense of fate's symmetry and neatness.
If this were all there is to roulette, of course, the casinos would simply be charities redistributing wealth from the proponents of red or odd to black or even and back again. The little extra that earns them everythingâis
nothing:
the zero that joins the 36 numbers on the wheel. It's not a magic numberâyou may bet on it if you wishâbut its presence subtly shifts the alignment of payoff and probability. Your bet on any one number pays 36 times, but the event happens only one time in 37. Your cautious chips on
rouge
or
impair
may double your stake; but either chance will come up, not half the time, but half minus 1/74.
nothing:
the zero that joins the 36 numbers on the wheel. It's not a magic numberâyou may bet on it if you wishâbut its presence subtly shifts the alignment of payoff and probability. Your bet on any one number pays 36 times, but the event happens only one time in 37. Your cautious chips on
rouge
or
impair
may double your stake; but either chance will come up, not half the time, but half minus 1/74.
Why would anyone possessed of his senses put even money on an uneven chance? Who would volunteer to pay a tax of 2.703 percentâfor that's what the discrepancy between chance and payout represents? Some see it as a fair fee for an evening's entertainment; it's like going to have one's sense of risk massaged. Others look more closely at the whole proposition andâby deconstructing the idea of probability it representsâmanage occasionally to make a killing.
Joseph Jaggers was a 43-year-old no-nonsense Lancashire cotton-spinning engineer; a man proof against gambling's seductive powers. When he arrived in Monte Carlo in 1873, he knew nothing about rouletteâbut everything about spindles. As laymen, we assume that the wheel, so silent and smooth, must spin true. Jaggers' professional life, though, was an unavailing struggle to
make
things spin true. There is no earthly mill where all hums perfectly on its axis. Machinery shares man's imperfections: it wobbles and chattersâto a practiced ear, intelligibly.
make
things spin true. There is no earthly mill where all hums perfectly on its axis. Machinery shares man's imperfections: it wobbles and chattersâto a practiced ear, intelligibly.
Jaggers hired six clerks to record every number generated at all the casino's tables for a week; he locked himself in with the results and found what he sought: one wheel had a distinct bias. The next day he arrived at the tables and began to play his advantage. After a day of heavy losses, the management switched the wheel to another table. But Jaggers was observant: puzzled at losing the next morning, he remembered a tiny scratch on “his” wheel that was no longer apparent. He looked for it among the other tables and was soon reunited with the untrue spindle. In all, he won the equivalent of $325,000 and then returned to Lancashire, never to gamble againâalthough in truth he had never been gambling at all.
The ball
must
land somewhere. The cup in which it finally nestles is the solution to a complex but mathematically determined sequence of collisions, each with its own precise possible description in terms of the angular momentum of its components. We call this solution “chance” because we assume that these collisions are complex enough and happen sufficiently quickly to make physics throw up its hands and accept that the only moment at which we can understand what has happened is after the sequence is finished. Yet if you could rewind time, the last bounce or two might be less difficult to predict than the whole sequence, assuming that you could gauge accurately the speed and spin of ball and wheel at that point. This was thought to have been the technique of Charles Deville Wells, The Man Who Broke the Bank at Monte Carlo.
must
land somewhere. The cup in which it finally nestles is the solution to a complex but mathematically determined sequence of collisions, each with its own precise possible description in terms of the angular momentum of its components. We call this solution “chance” because we assume that these collisions are complex enough and happen sufficiently quickly to make physics throw up its hands and accept that the only moment at which we can understand what has happened is after the sequence is finished. Yet if you could rewind time, the last bounce or two might be less difficult to predict than the whole sequence, assuming that you could gauge accurately the speed and spin of ball and wheel at that point. This was thought to have been the technique of Charles Deville Wells, The Man Who Broke the Bank at Monte Carlo.
Claude Shannon, MIT's deviser of information theory, thought the same computers that solved the equations of missile trajectory could master the wheel, so he built one in his basement. Norman Packard and Doyne Farmer followed in his footsteps; their 1980 shoe-mounted computer, the Eudaemonic Pie, attempted to solve the equations of motion for those last moments between the slowing of the ball and the closing of the bets. Despite its puny 4K processor, it worked too well for the comfort of Las Vegas casino owners; it is now a felony in Nevada to enter a gaming place with a computer in your shoe. Roulette's simplicity, its plain-sight mechanism, provides a constant temptation to seek out an eddy of determinism in the flow of randomness.
All this, though, is to miss the point of gambling, which is to accept the imbalance of chance in general yet deny it for the here and now. Individually we know, with absolute certainty, that “the way things happen” and what actually happens to
us
are as different as sociology and poetry. Our personal story has meaning: what happens to us is fate, not mere occurrence. We challenge destiny at the tables; and when we climb those carpeted steps, we are going to battle.
us
are as different as sociology and poetry. Our personal story has meaning: what happens to us is fate, not mere occurrence. We challenge destiny at the tables; and when we climb those carpeted steps, we are going to battle.
Â
“I think about four hundred gold fredericks must have come into my hands in some five minutes. That was when I should have left, but a strange sensation came over me, a kind of challenge to fate, a sort of desire to give it a fillip, to stick my tongue out at it.” Dostoevsky's
The Gambler
was originally titled
Roulettenburg
âand it was a world he knew well. Wiesbaden, Bad Homburg, Baden-Badenâall the German spas regularly welcomed the intense, red-haired Russian with his increasingly unhappy wife. He would usually arrive filled with confidence, win moderately and briefly, and then dissolve calamitously into loss, guilt, and misery. Loss to Dostoevsky, as to many gamblers, was an aberration: the surprising local failure of an otherwise well-designed system. Its message was not “don't try to beat the house” but “you're nearly there; another minor adjustment and it will work perfectly.”
The Gambler
was originally titled
Roulettenburg
âand it was a world he knew well. Wiesbaden, Bad Homburg, Baden-Badenâall the German spas regularly welcomed the intense, red-haired Russian with his increasingly unhappy wife. He would usually arrive filled with confidence, win moderately and briefly, and then dissolve calamitously into loss, guilt, and misery. Loss to Dostoevsky, as to many gamblers, was an aberration: the surprising local failure of an otherwise well-designed system. Its message was not “don't try to beat the house” but “you're nearly there; another minor adjustment and it will work perfectly.”
From space the ocean looks like a smooth blue shell; from an airplane, we see an irregular surface like hammered metal; on a raft in a storm, we know only that this wave is upon us and that one is comingâyet we still try to see the pattern of our misfortune and gain advantage from local predictions. The long run reveals the house advantageâbut why should we wait for the long run? Life is of the minute; why shouldn't we seize and exploit departures from the trend?
Other books
Dead Magic by A.J. Maguire
The French Promise by Fiona McIntosh
Jack on the Tracks by Jack Gantos
One Prayer Away by Kendra Norman-Bellamy
Where The Sidewalk Ends by Silverstein, Shel
THE MILLIONAIRE AND THE LIBRARIAN by Scott, J.S.
A Dagger of the Mind (The Imperial Metals) by Daniel Antoniazzi
Uncle Abner, Master of Mysteries by Melville Davisson Post
Frames by Loren D. Estleman
Crimson Footprints lll: The Finale by Pugh, Shewanda