Alan Turing: The Enigma (48 page)
Read Alan Turing: The Enigma Online
Authors: Andrew Hodges
Tags: #Biography & Autobiography, #Science & Technology, #Computers, #History, #Mathematics, #History & Philosophy

This was not a new idea. The theory of games had been studied mathematically since the 1920s, and this principle, second nature to chessplayers,
*
had been abstracted and formalised in the manner of modern mathematics. The word ‘minimax’ had been coined for the idea of the least bad course of action. It applied not only to games like chess, but also to those which involved guessing and bluffing. Much of the mathematical work had been done by von Neumann, taking up ideas first published by the French mathematician E. Borel in 1921. Borel had defined ‘pure’ and ‘mixed’ strategies in game-playing. Pure strategies were definite rules, setting out the proper action in any contingency; a mixed strategy would consist of two or more different pure strategies, to be chosen at random, but
with specified probabilities for each strategy according to the contingency.
Von Neumann had been able to show that for any game with two players, with fixed rules, there would exist optimal strategies, usually mixed, for each player. Alan would very likely have attended his talk on the game of Poker, given at Princeton in 1937, which illustrated the result.
33
It was von Neumann’s beautiful, if depressing theorem, that in
any
two-person game
*
both players would be locked into their ‘minimax’ strategies, both finding that all they could do was to make the best of a bad job, and to give the opponent the worst of a good job, and that these two objectives would always coincide.
Poker, with its bluffing and guessing, was a better illustration of the von Neumann theory than chess.
†
A game without concealment, such as chess, von Neumann called a game of ‘perfect information’, and he proved that any such game would always possess an optimal ‘pure strategy’. In the case of chess, this would be a complete set of rules for what to do in every contingency. There being far more possible chess positions than plugboard positions for the Enigma, however, the general von Neumann theory had nothing of practical value to say about the game. It was an example of where a high-powered, abstract approach failed to be of use. Alan and Jack Good’s approach was quite different in nature, being for one thing concerned not so much with a theory of the game, but with a discussion of human thought processes. It was an
ad hoc
discussion, ‘dull and elementary’ by pure-mathematical standards, and pursued quite independently of the existing theory of games. They could have done it at school.
In their analysis it first had to be assumed that there was some sensible scoring system, awarding a numerical value to the various possible future positions on the basis of pieces held, pieces threatened, squares controlled and so forth. With this agreed, the most crude ‘definite method’ would be simply to make the move that maximised the score. The next level of refinement would take the opponent’s reply into account, using the ‘minimax’ idea to choose the ‘least bad’ move. In chess there would normally be about thirty possible moves for each player, so that even this crude system would require about a thousand separate assessments. A further step of looking ahead would require thirty thousand.
Reducing the figure of thirty to a mere two for the sake of a diagram, the player (White) making a three-move look-ahead is confronted by a ‘tree’ such as:
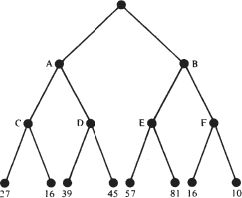
Current position, W to play
Position resulting from the 2 possible W moves
Position resulting from the possible replies
Position resulting from the possible W replies. These positions are evaluated by scoring.
A human playing White might reason that it would be good to reach position E, but Black will not be so obliging, and will respond to move B by reply F. A second best, for White, would be position D, but again it must be assumed that Black will play C to prevent this. Of the two evils, positions C and F, C is the lesser one, since at least it guarantees for White a position of value 27. So White plays move A.
A ‘machine’ could simulate this train of thought by a method of ‘backing up’ the tree. Having worked out all the scores for three moves ahead, it would then label the intermediate positions on a minimax basis. It would assign 27 to C, 45 to D, 81 to E, 16 to F (the
best
in each case), then 27 to A, 16 to B (the
worst
in each case), and finally select move A for White.
This basic idea created a ‘machine’ that could effect a decision procedure bearing some relation to human intelligence. It was small beer compared with the Hilbert problem, which had required thinking about decision procedures for the whole of mathematics. But on the other hand, it was something that could actually work. As a practical model for mechanical ‘thinking’ it fascinated Alan to the point of obsession.
Such a three-move analysis would be hopelessly ineffective in real chess, in which players would think not in terms of moves but of
chains
of moves, as for example when a sequence of obligatory captures was set in motion. Alan and Jack Good saw this and decided that the ‘look-ahead depth’ would have to be variable, continuing as
far as any capture was possible at all, so that evaluations would only be made on ‘quiescent’ positions. Even so, such a scheme would fail to cope with more subtle play, involving traps leading to pins or forks, a fact which they discussed. It was a crude, brute force attack on chess-playing, but it was a first step in mechanising a fairly sophisticated thought process – at least, a first non-secret step.
They thought these ideas too obvious to be worth publishing. Alan did, however, continue to pursue his own mathematical work and to submit it for publication in America. A true intellectual, he would have been ashamed to let human crime and folly defeat him. ‘Before the war my work was in logic and my hobby was cryptanalysis,’ he once said, ‘and now it is the other way round.’ He had to thank Newman for stimulating his thoughts on this ‘hobby’ of mathematical logic, for they corresponded
34
in 1940 and 1941, in which latter year Newman again gave Cambridge lectures on Foundations of Mathematics.
Most of Alan’s
efforts were directed towards a new formulation of the theory of types. Russell had regarded types as rather a nuisance, adopted
faute de mieux
in order to save Frege’s set theory. Other logicians had felt that a hierarchy of logical categories was really quite a natural idea, and that it was the attempt to lump together every conceivable entity into ‘sets’ that was strange. Alan inclined to the latter view. He would prefer a theory which agreed with the way in which mathematicians actually thought, and which worked in a practical way. He also wanted to see mathematical logic used to make the work of mathematicians more rigorous. In a less technical essay written in this period,
35
‘The Reform of Mathematical Notation’, he explained that despite all the efforts of Frege and Russell and Hilbert
… mathematics has profited very little from researches in symbolic logic. The chief reason for this seems to be a lack of liaison between the logician and the mathematician-in-the-street. Symbolic logic is a very alarming mouthful for most mathematicians, and the logicians are not very much interested in making it more palatable.
His own effort to bridge the gap began with an attempt
… to put the theory of types into a form in which it can be used by the mathematician-in-the-street without having to study symbolic logic, much less use it. The statement of the type principle given below was suggested by lectures of Wittgenstein, but its shortcomings should not be laid at his door.
The type principle is effectively taken care of in ordinary language by the fact that there are nouns as well as adjectives. We can make the statement ‘All horses are four-legged’, which can be verified by examination of every horse, at any rate if there are only a finite number of them. If however we try to use words like ‘thing’ or ‘thing whatever’ trouble begins. Suppose we understand ‘thing’ to include everything whatever, books, cats, men, women, thoughts, functions of men with cats as values, numbers, matrices, classes of classes, procedures, propositions… Under these circumstances what can we make of the statement ‘All things are not prime multiples of 6’…. What do we mean by it? Under no circumstances is the number of things to be examined finite. It may be that some meaning can be given to statements of this kind, but for the present we do not know of any. In effect then the theory of types requires us to refrain from the use of such nouns as ‘thing’, ‘object’ etc., which are intended to convey the idea ‘anything whatever’.
The technical work of separating mathematical ‘nouns’ from ‘adjectives’ was based upon that of Church, whose lectures he had followed at Princeton, and who published a description of his type theory in 1940. Part of Alan’s work was done in collaboration with Newman through correspondence; their joint paper
36
being received at Princeton on 9 May 1941. It
must have crossed the Atlantic just as the
München
was captured. Alan produced a further paper
37
of a highly technical nature,
The Use of Dots as Brackets in Church’s system
, and submitted it just a year later. This promised as forthcoming two more papers, but these never emerged.
He did not allow the war to expunge the idea that, for mathematics, the world should be a single country. In a letter to Newman of autumn 1941, concerned with arrangements for sending out reprints of their paper, he commented: ‘Also expect they might send a copy to Scholz, but I expect that will be impossible by then.’
This was not the only thing that became impossible in the course of 1941. The engagement had continued during the summer, but there had been signs of inner conflict on Alan’s part. Once they had a weekend together in Oxford, visiting Joan’s brother there; Alan went off by himself for a while, apparently thinking it over again, though deciding to carry on. Then in the last week of August they were able to have a whole week together. (They were allowed a week of leave each quarter.) They took their holiday in North Wales, going up by train from Bletchley with bicycles and rucksacks, and arriving at Portmadoc when it was already dark. Alan had arranged for them to stay at a hotel, but the management had made a mess of it and overbooked; only by making a fuss could they be accommodated for the night, and they lost half a precious day finding another place in the morning. Food was a problem too, Alan not having a temporary ration card. But they had brought some margarine, and managed on bread and a surprise discovery of unrationed meat paste. They walked the lesser mountains, the same as he had tramped as a boy: Moelwyn Bach, Cnicht, and others, suffering only the usual troubles with punctures and rain.
It was soon after they returned that Alan made up his mind and burnt his bridges. It was neither a happy nor an easy decision. He quoted to her Oscar Wilde’s words, the closing lines from
The Ballad of Reading Gaol
, which bore both an immediate and a prophetic interpretation:
Yet each man kills the thing he loves,
By each let this be heard,
Some do it with a bitter look,
Some with a flattering word,
The coward does it with a kiss,
The brave man with a sword!
There had been several times when he had come out with ‘I do love you’. Lack of love was not Alan’s problem. The break created a difficult situation in the Hut. Alan told Shaun Wylie that the engagement had been broken off, but not the true reason. In fact he used a dream to make up an explanation, saying that he had dreamt that they had gone to Guildford together and that Joan had not been accepted by his family. Alan dropped out of shift work so that he and Joan did not have to meet more often than
necessary at first. It was very upsetting for both of them, but he had behaved in such a way that she knew she had not been rejected as a person. The break was a barrier, but the understanding of it continued as a link.
As they talked about games at Bletchley, something of that locked-in minimax logic of combat was developing out on the Atlantic, strategy forcing counter-strategy, weapon forcing counter-weapon, detection forcing counter-detection. Less tidy than poker or chess, these real conflicts involved rules which were always changing, strategies whose consequences could not be foreseen, and losses which were more than marks on paper. But like poker, the U-boat war was a game of imperfect information, with bluffing and guessing. It was also a game in which, by August 1941, the British had placed a mirror behind the opponent’s hand, and was able to cheat by looking at almost all the German cards.
*
There was no need for further captures in the rest of 1941, and decryption was performed by Hut 8 within a period of thirty-six hours – this despite the fact that the eight rotors of the naval Enigma had 336 possible orders, as compared with the 60 of the other services’ machines.