Alan Turing: The Enigma (94 page)

The picture of the cortex as an unorganised machine is very satisfactory from the point of view of evolution and genetics. It clearly would not require any very complex system of genes to produce something like the … unorganised machine. In fact this should be much easier than the production of such things as the respiratory centre. …

Somehow the brain did it, and somehow brains came into being every day without all the fuss and bother of the minnow-brained ACE. There were two possibilities: either a brain learnt to think by dint of interaction with the world, or else it had something written in it at birth – which must be programmed, in a looser sense, by the genes. Brains were too complicated to consider at first. But how did anything know how to grow? There lay the question – a question that the smallest child could ask, and the question that
Natural Wonders Every Child Should Know
had placed at the centre. When embarking upon the delicate subject of ‘what little boys and girls are really made of’, E.T. Brewster had launched into a description of the growth of starfish, beginning with
the young egg, before there is any sign of a growing creature inside. One would perhaps expect to see the oil and jelly mixture change gradually into a star-fish. Instead of this, however, this little balloon-like affair splits squarely into two, and makes two little balloons just alike, and which lie side by side. … In about half an hour, each of these balloons or bubbles, ‘cells’ as they have come to be called, has divided again; so that now there are four. The four soon become eight; the eight, sixteen. In the course of a few hours, there are hundreds, all sticking together and all very minute; so that the whole mass looks like the heap of soap bubbles which one blows by putting the pipe under the surface of the soap suds.

From this sphere of cells, Brewster explained, the animal would take shape:

If it is an animal like ourselves, this body stuff, before it becomes a body, is a round ball. A furrow doubles in along the place where the back is to be, and becomes the spinal cord. A rod strings itself along underneath this, and becomes the back-bone. The front end of the spinal cord grows faster than the rest, becomes larger, and is the brain. The brain buds out into the eyes. The outer surface of the body, not yet turned into skin, buds inward and makes the ear. Four outgrowths come down from the forehead to make the face. The limbs begin as shapeless knobs, and grow out slowly into arms and legs. …

Alan had thought about embryology all the time, fascinated by the fact that how such growth was determined was something ‘nobody has yet made the smallest beginning at finding out.’ There had been little advance since
Growth and Form
, the 1917 classic that he had read before the war. The 1920s had made it possible to invoke the Uncertainty Principle to suggest that life was intrinsically unknowable, like the simultaneous measurement of position and velocity in quantum mechanics.
⁴²
As with minds, there was an aura of religion and magic around the subject that attracted the attention of his scepticism. It was a fresh field. C.H. Waddington’s 1940 standard work
⁴³
on embryology did no more than list experiments on growing tissue, to explain in what circumstances it seemed to know what to do next.

The greatest puzzle was that of how biological matter could assemble itself into patterns which were so enormous compared with the size of the cells. How could an assemblage of cells ‘know’ that it must settle into a fivefold symmetry, to make a starfish? How was this symmetry communicated across millions of cells? How could the Fibonacci pattern of a fir cone be imposed in its harmonious, regular way upon the growing plant? How could matter
take shape
or, as biological Greek had it, what was the secret of
morphogenesis
? Suggestive words like ‘morphogenetic field’, vague as the Life Force, were employed by biologists to describe the way that embryonic tissue seemed to be endowed with an invisible pattern which subsequently dictated its harmonious development. It had been conjectured that these ‘fields’ could be described in chemical terms – but there was no theory of
how this could be.
^*
Polanyi believed that there was
no
explanation except by a guiding
esprit de corps
; the inexplicability of embryonic form was one of his many arguments against determinism.
⁴⁵
Conversely, Alan told Robin that his new ideas were intended to ‘defeat the Argument from Design’.

Alan was familiar with Schrödinger’s 1943 lecture,
What is Life
, which deduced the crucial idea that genetic information must be stored at molecular level, and that the quantum theory of molecular bonding could explain how such information could be preserved for thousands of millions of years. At Cambridge, Watson and Crick were busy in the race against their rivals to establish whether this was really so, and how. But the Turing problem was not that of following up Schrödinger’s suggestion, but that of finding a
parallel
explanation of how, granted the production of molecules by the genes, a chemical soup could possibly give rise to a biological pattern. He was asking how the information in the genes could be translated into action. Like Schrödinger’s contribution, what he did was based on mathematical and physical principle, not on experiment; it was a work of scientific imagination.

There were other suggestions in the literature for the nature of the ‘morphogenetic field’, but at some point Alan decided to accept the idea that it was defined by some variation of chemical concentrations, and to see how far he could get on the basis of that one idea. It took him back to the days of the iodates and sulphites, to the mathematics of chemical reactions. But the new problem was of another order. It was not merely to examine substance A changing into substance B, but to discover circumstances in which a mixture of chemical solutions, diffusing and reacting with each other, could settle into a pattern, a pulsating pattern of chemical waves; waves of concentration into which the developing tissue would harden; waves which would encompass millions of cells, organising them into a symmetrical order far greater in scale. This was the fundamental idea, parallel to Schrödinger’s – that a chemical soup could contain the information required to define a large-scale chemical pattern in space.

There was one central, fundamental problem. It was exemplified in the phenomenon of
gastrulation
. This was the process described and illustrated in
Natural Wonders
, in which a perfect sphere of cells would suddenly develop a groove, determining the head and tail ends of the emergent animal. The problem was this: if the sphere were symmetrical, and the chemical equations were symmetrical, without knowledge of left or right, up or down, where did this
decision
come from? It was just such a phenomenon that inspired Polanyi to claim that some immaterial force must be at work.

In some way information was being
created
at this point, and this went against what was normally
expected. When the lump of sugar has been dissolved in the tea, no information remains, at the chemical level, as to where it was. But in certain phenomena, those of crystallisation for instance, the reverse process could occur. Pattern could be created, rather than destroyed. The explanation lay in the interplay of more than one level of scientific description. In the
chemical
description, in which only average concentrations and pressures would be considered, no spatial direction would be preferred to any other. But at a more detailed, Laplacian level, the individual motions of the molecules would not be perfectly symmetrical, and under certain conditions, like that of the crystallising liquid, could serve to pick out a direction in space. The example Alan chose as illustration was drawn from his electrical experience:
⁴⁶

The situation is very similar to that which arises in connexion with electrical oscillators. It is usually easy to understand how an oscillator keeps going when once it has started, but on a first acquaintance it is not obvious how the oscillation begins. The explanation is that there are random disturbances always present in the circuit. Any disturbance whose frequency is the natural frequency of the oscillator will tend to set it going. The ultimate fate of the system will be a state of oscillation at its appropriate frequency, and with an amplitude (and a wave form) which are also determined by the circuit. The phase of the oscillation alone is determined by the disturbance.

He set up a system of oscillating circuits in his office, and used to show people how they would gradually all come to resonate with each other.

Such a process of toppling, or crystallising, or falling into some pattern of oscillation, could be described as the resolution of an unstable equilibrium. In the case of the developing sphere of cells, it would have to be shown that in some way, through a change in temperature or the presence of a catalyst, the stable chemical balance could suddenly become unstable. It would be the chemical equivalent of piling the last straw on the camel’s back. Alan’s own analogy was that of a mouse climbing up a pendulum.

Here was an idea which might explain something about how the information in the genes could be translated into physiology. The problem of growth as a whole would be far, far more complicated than this. But analysis of this moment of creation might yield a clue as to how the harmony and symmetry of biological structures could suddenly appear, as if by magic, out of nothing.

To examine this moment of crisis mathematically, one had to approximate over and over again. He had to ignore the internal structure of the cells, and forget that the cells would themselves be moving and splitting as the patterning process took place. There was also an obvious limitation to the chemical model. How was it that the human heart was always on the left hand side? If this symmetry-breaking of the primordial sphere were determined at random, then hearts would be equally distributed between left and right. He had to leave this problem on one side, with a conjecture that at some point the asymmetry of the molecules themselves would play a part.

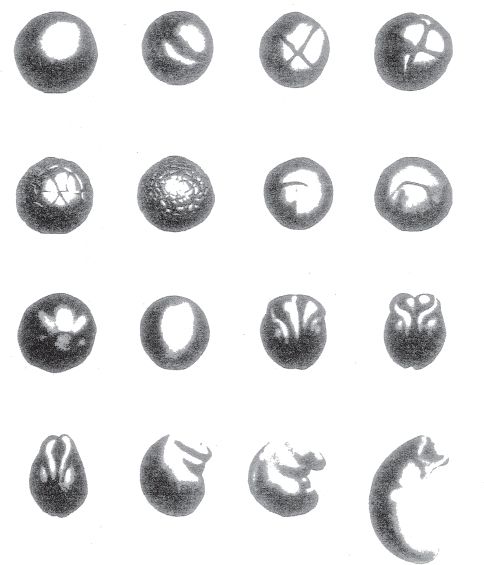
The process of gastrulation, essentially as revealed in
Natural Wonders
.

But with these reservations, his approach was to take the model and try it out. As he wrote,
⁴⁷
in a classic statement of the scientific method:

… a mathematical model of the growing embryo will be described. This model will be a simplification and an idealization, and consequently a falsification. It is to be hoped that the features retained for discussion are those of greatest importance in the present state of knowledge.

The result was applied mathematics
par excellence
. Just as the simple idea of the Turing machine had sent him into fields beyond the boundaries of Cambridge mathematics, so now this simple idea in physical chemistry took him into a region of new mathematical problems. But this time at least it was all his own work. No one else could make a mess of it for him.

Even with immense simplifications, the mathematical equations corresponding to a soup of only four interacting chemical solutions, were still
too intractable. The problem was that chemical reactions were ‘non-linear’. The equations for electricity and magnetism were ‘linear’, meaning that if two electromagnetic systems were superimposed (as for example when two radio transmitters radiated simultaneously), then the effects would simply be additive. The two transmitters would not interfere with each other. But chemistry was quite different. Double the concentration of reactants, and the reaction might go four times as fast. Superimpose two solutions, and anything might happen! Such ‘non-linear’ problems had to be solved as a whole, and not by the mathematical methods familiar in electromagnetic theory, those of describing the system as the sum of many little bits. However, that critical moment of budding, at the instant when the unstable system crystallised into a pattern, could be treated as if it were a ‘linear’ process – a fact familiar to applied mathematicians, and one which gave him a first handle upon the problem of growth.

So he had his hands on another central problem of life, this time not of the mind, but of the body, although both questions were related to the brain. He quite literally had his hands upon it, for he had always enjoyed examining plants when on his walks and runs, and now he began a more serious collection of wild flowers from the Cheshire countryside, looking them up in his battered
British Flora
,
⁴⁸
pressing them into scrapbooks, marking their locations in large scale maps, and making measurements. The natural world was overflowing with examples of pattern; it was like codebreaking, with millions of messages waiting to be decrypted. Like codebreaking, the field was open-ended; with his chemical model he had one sharp tool to apply to it, but that was only the beginning.