Alan Turing: The Enigma (38 page)

Alternatively, a cipher system might be based upon the ‘substitution’ idea. In its simplest form, this was used for puzzle-page cryptograms, such as they had solved in Princeton treasure hunts. It meant that one letter of the alphabet would be substituted for another, according to some fixed rule like:

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

K S G J T D A Y O B X H E P W M I Q C V N R F Z U L

so that TURING would become VNQOPA. Such a simple, or ‘mono-alphabetic’ cipher could easily be solved by looking at letter frequencies, common words, and so forth, and in fact the only point of puzzle-page problems was that the setter would include peculiar words like XERXES to make this difficult. Such a system would be too simple-minded for military application. But there were systems in use in 1939 which were not much more advanced. One sophistication lay in the use of several alphabetic substitutions, used in rotation or according to some other simple scheme. The few manuals and text-books
³
of cryptology in existence devoted themselves mainly to such ‘poly-alphabetic’ ciphers.

Slightly more complex was the use of a system which substituted not for single letters, but for the 676 possible letter pairs. One British cipher system of this period was of this nature, combining the idea with the use of a code book. It was used by the Merchant Navy.
⁴

The
cipher clerk would first have to render the message into Merchant Navy Code, thus:

The next step required an even number of rows, so the clerk would have to add a nonsense word to make it up:

Then the encipherment would be done. The clerk would take the first vertical pair of letters, here VC, and look it up in a table of letter pairs. The table would specify some other pair, say XX. The clerk would continue to go through the message, substituting for each letter pair in this way.

There was little more to it, except that as with the ‘adding on’ kind of cipher, the process was futile unless the legitimate receiver knew which substitution table was being used. To preface the transmission with ‘Table number 8’, say, would allow the enemy analyst to collect and collate the transmissions enciphered with the same table, and make an attack. There had to be some element of disguise involved. So printed with the table there was another list of eight-letter sequences such as ‘BMTVKZMD’. The clerk would choose one of these sequences and add it to the beginning of the message proper. The receiver, equipped with the same list, could then see which table was being used.

This simple rule illustrated a very general idea. In practical cryptography, as opposed to the setting of isolated puzzles, there would usually be some part of the message transmitted which did not convey the text itself, but which conveyed instructions on how to decipher it. Such elements of the transmission, which would be disguised and buried within it, were called
indicators
. Even a one-time pad system might employ indicators, to give a check on which page of the pad was being used. In fact, unless everything were spelt out in advance and in complete, rigid, detail, without any chance of ambiguity or error, there would have to be some form of indicator.

It must surely have struck Alan, who had been thinking at least since 1936 about ‘the most general kind of code or cipher’, that this mixing of instructions and data within a transmission was reminiscent of his ‘universal machine’, which would first decipher the ‘description number’ into an instruction, and then apply that instruction to the contents of its tape. Indeed
any
cipher system might be regarded as a complicated ‘mechanical process’ or Turing machine, involving not just the rules for adding or substituting, but rules for how to find, apply and communicate the method of encipherment itself. Good cryptography lay in the creation of an entire body of rules, not in this or that message. And serious cryptanalysis consisted of the work of recovering them; reconstructing the entire mechanical process which the cipher clerks performed, through an analysis of the entire mass of signals.

Maybe
the Merchant Navy cipher system was not the last word in baffling complexity, but for operational use in ordinary ships, it was near the limit of practicality for hand methods. Anyone might dream up more secure systems, but if a ciphering operation became too long and complicated, it would only result in more delays and mistakes. However, if cipher machines were used, to take over part of the clerk’s ‘mechanical process’, the situation could be very different.

In this respect Britain and Germany were running a symmetrical war, using very similar machines. Virtually every German official radio communication was enciphered on the Enigma machine. The British state relied, less totally, on the Typex. This machine was used throughout the army and in most of the RAF; the Foreign Office and the Admiralty retained their own hand systems depending on books. Enigma and Typex alike mechanised the basic operations of substitution and adding on, in such a way that a more complex system came within practical grasp. They did nothing that could not have been done by the looking up of tables in books, but enabled the work to be done more quickly and accurately.

There was no secret about the existence of such machines. Everyone knew of it – everyone, at least, who had a 1938 edition of Rouse Ball’s
Mathematical Recreations and Essays
as a school prize. A revised chapter written by the U.S. Army cryptanalyst, Abraham Sinkov, wheeled out all the antiquated grilles, Playfair ciphers, and so forth, but also mentioned that

Quite recently there has been considerable research carried on in an attempt to invent cipher machines for the automatic encipherment and decipherment of messages. Most of them employ periodic polyalphabetic systems.

A ‘periodic’ polyalphabetic cipher would run through some sequence of alphabetic substitutions, and then repeat that sequence.

The most recent machines are electrical in operation, and in many cases the period is a tremendously large number.… These machine systems are much more rapid and much more accurate than hand methods. They can even be combined with printing and transmitting apparatus so that, in enciphering, a record of the cipher message is kept and the message transmitted; in deciphering, the secret message is received and translated, all automatically. So far as present cryptanalytic methods are concerned, the cipher systems derived from some of these machines are very close to practical unsolvability.

Nor
was there anything secret about the basic Enigma machine. It had been exhibited in 1923, soon after its invention, at the congress of the International Postal Union. It was sold commercially and used by banks. In 1935 the British had created Typex by adding certain attachments to it, while a few years earlier the German cryptographic authorities had modified it in a different way to create the machine which, though bearing the original name of Enigma, was much more effective than the commercially available device.

This did not mean that the German Enigma with which Alan Turing now had to grapple, was something ahead of its time, or even the best that the technology of the late 1930s could have produced. The only feature of the Enigma that brought it into the twentieth century, or at least the late nineteenth, was that it was indeed ‘electrical in operation’. It used electrical wirings to perform automatically a series of alphabetical substitutions, as shown in the first figure. But an Enigma would be used in a fixed state only for enciphering
one
letter, and then the outermost rotor would move round by one place, creating a new set of connections between input and output, as shown in the second figure.

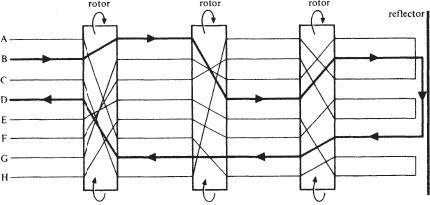
The Basic Enigma

For the sake of simplicity, the diagram has been drawn for an alphabet of only eight letters, although in fact the Enigma worked on the ordinary 26-letter alphabet. It shows the state of the machine at some particular moment in its use. The lines marked correspond to current-carrying wires. A simple switch system at the input has the effect that if a key (say the B key) is depressed, a current flows (as shown in the diagram by bold lines) and lights up a bulb in the output display panel (in this case, under the letter D). For the hypothetical 8-letter Enigma, the next state of the machine would be:

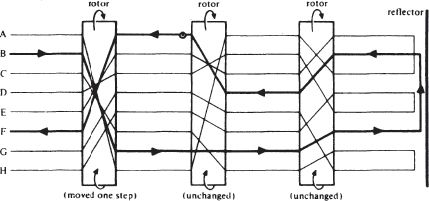
For
the 26-letter Enigma, there would be 26 × 26 × 26 = 17576 possible states of the rotors. They were geared essentially
^*
like any kind of adding machine or comptometer, so that the middle rotor would move on one step when the first had made a complete revolution, and the innermost move a step when the middle one had made a complete turn. The ‘reflector’, however, would not move, it being a fixed set of wires connecting the outputs of the innermost rotor.

So the Enigma was polyalphabetic, with a period of 17576. But this was not a ‘tremendously large number’. Indeed, it would require a book only the size of a ready reckoner for all the alphabets to be written out. This mechanism was not, in itself, a leap into a new degree of sophistication. There was also a warning sounded by Rouse Ball in the old 1922 edition of his book that Alan had studied at school:

The use of instruments giving a cipher, which is or can be varied constantly and automatically, has often been recommended … but the risk of some instrument … falling into unauthorized hands must be taken into account. Since equally good ciphers can be constructed without the use of mechanical devices I do not think their employment can be recommended.

For what was done by a machine might all the more easily be undone by a machine. The inner complexity of the Enigma, however clever it might look, would be worthless unless it created a cipher system which could not be broken even by an enemy in possession of a copy of the machine. It might only serve to give a false sense of security.

Nor was the technical construction of the Enigma as advanced as that suggested by Sinkov’s description of contemporary developments. The cipher clerk using it still had the tedious and time consuming task of noting which letter had been illuminated, and writing it down. There was no automatic printing or transmission, which had to be done laboriously in Morse code. Far from being a weapon of the modern Blitzkrieg, this plodding device drew on nothing more technologically advanced than the electric light bulb.

From
the cryptanalyst’s point of view, however, the physical labours of the cipher clerk, and the physical construction of the machine, were irrelevant. What mattered was the
logical
description – just like a Turing machine. Everything relevant to the Enigma was contained in its ‘table’, a list of its states and what it would do in each state. And from a logical point of view, the action of the Enigma, in any given, fixed, state, enjoyed a very special property. It was a symmetrical property inherent in the ‘reflecting’ nature of the machine. For any Enigma, in any state, it would be true that if A were enciphered into E, then in that same state, E would be enciphered as A. The substitution alphabets resulting from an Enigma state would always be
swappings
.

For the hypothetical 8-letter machine in the state shown in the first diagram, the substitution would be:

For the machine in the state shown in the second diagram, it would be:

These could be written as swappings: (AE) (BD) (CG) (FH) in the first case and (AE) (BF) (CG) (DH) in the second.