Alan Turing: The Enigma (41 page)

Travis introduced Jones to Alan, who ‘liked the idea’. But with the Enigma, at least, the central method remained on entirely different lines. It kept to the idea of exploiting a known piece of plain-text. The difficulty, of course, was that the military Enigma
did
use a plugboard, which rendered such a naive searching process impossible, there being 150,738,274,937,250 possible ways
^*
of connecting ten pairs of letters. In no way could a machine run through them all.

Yet no serious analyst would be daunted by this frightening number. Large numbers would not in themselves guarantee immunity from attack. Anyone who had solved a puzzle-page cryptogram had succeeded in-eliminating all but one of the 403,291,461,126,605,635,584,000,000 different alphabetic substitutions.
^†
It could be done because such facts as that E was common, AO rare, and so forth, would each serve to eliminate vast numbers of possibilities at once.

It can be seen that the sheer number of plugboards is not in itself the problem, by considering an entirely hypothetical machine, in which a plugboard swapping is applied only
before
encipherment by a basic Enigma. Suppose that for such a machine, it is known for certain that the cipher-text FHOPQBZ is the encipherment of GENERAL.

Once again, it would be possible to feed the letters FHOPQBZ into seven consecutive Enigmas, and examine the output. But this time, one could not expect the letters GENERAL to emerge, for an unknown plugboard swapping would have been applied to those letters. Nevertheless, something could still be done. Suppose that at some point in the process of running through all the rotor positions, the set-up happens to be:

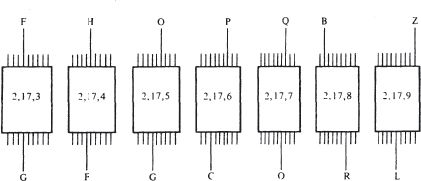
Then it may be asked whether the letters GFGCORL could, or could not, be obtained from GENERAL by the effect of a plugboard swapping. In this example, the answer is ‘no’, since no swapping could leave the first G unchanged, but swap the second G into an N; no swapping could turn the first E of GENERAL into an F and the second into a C. Furthermore, no swapping could change the R of GENERAL into an O, but then change the A into an R. Any one of these observations suffices to rule out that particular rotor position.

One way of thinking of this question is in terms of consistency. Having fed the cipher-text into the Enigmas, is the output consistent with the known plain-text, in that it differs only by virtue of swapping? From this point of view, the correspondences (OR) and (RA), or (EF) and (EC), are
contradictions
. A single contradiction is enough to eliminate all the billions of possible plugboards, on this hypothetical machine. Sheer numerical size, therefore, may be insignificant, compared with the logical properties of the cipher system.

The crucial discovery was that something like this could be done for the actual military Enigma, with its plugboard swapping taking place both before and after entry into the rotors of the basic Enigma. But the discovery was not immediate, nor
was it the product of a single brain. It required a few months, and there were two figures primarily involved. For while Jeffries looked after the production of the new perforated sheets, the other two mathematical recruits, Alan and Gordon Welchman, were responsible for devising what became the British Bombe.
⁹

It was Alan who had begun the attack, Welchman having been assigned to traffic analysis, and so it was he who first formulated the principle of mechanising a search for logical consistency based on a ‘probable word’. The Poles had mechanised a simple form of recognition, limited to the special indicator system currently employed; a machine such as Alan envisaged would be considerably more ambitious, requiring circuitry for the simulation of ‘implications’ flowing from a plugboard hypothesis, and means for recognising not a simple matching, but the appearance of a contradiction.

The Turing Bombe

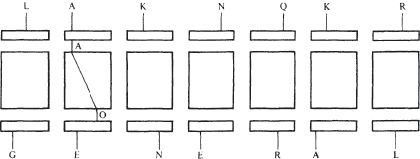
Suppose now that the letters
LAKNQKR are known to be the encipherment of GENERAL on the full Enigma with plugboard. This time there is no point in trying out LAKNQKR on the basic Enigmas, and looking at what emerges, for some unknown plugboard swapping must be applied to LAKNQKR before it enters the Enigma rotors. Yet the quest is not hopeless. Consider just one letter, the A. There are only 26 possibilities for the effect of the plugboard on A, and so we can think about trying them out. We may start by taking the hypothesis (AA),
i.e
. the supposition that the plugboard leaves the letter A unaffected.

What follows is an exploitation of the fact that there is only one plugboard, performing the same swapping operation on the letters going into the rotors as on the letters coming out. (If the Enigma had been fitted with two different plugboards, one swapping the ingoing letters and one the outcoming, then it would have been a very different story.) It also exploits the fact that this particular illustrative ‘crib’ contains a special feature – a closed loop. This is most easily seen by working out the deductions that can be made from (AA).

Looking at the second letter of the sequence, we feed A into the Enigma rotors, and obtain an output, say O. This means that the plugboard must contain the swapping (EO).

Now looking at the fourth letter, the assertion (EO) will have an implication for N, say (NQ); now the third letter will give an implication for K, say (KG).

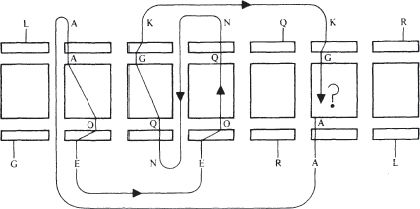
Finally we consider the sixth letter: here the loop closes and there will either be a consistency or a contradiction between (KG) and the original hypothesis (AA). If it is a contradiction, then the hypothesis must be wrong, and can be eliminated.

This method was far
from ideal. For it depended absolutely upon finding closed loops in the ‘crib’, and not all cribs would exhibit this phenomenon.
^*
But it was a method that would actually work, for the idea of completing a closed circuit was one that could be translated naturally into an electrical form. It showed that the sheer number of plugboards was not, in itself, an insuperable barrier.

It was a start, and it was Alan’s first success. Like most wartime scientific work, it was not so much that it needed the most advanced knowledge of the day. It was rather that it required the same kind of skill that was used in advanced research, but applied to more elementary problems. The idea of automating processes was familiar enough to the twentieth century; it did not need the author of
Computable Numbers
. But his serious interest in mathematical machines, his fascination with the idea of working like a machine, was extraordinarily relevant.
^†
Again, the ‘contradictions’ and ‘consistency’ conditions of the plugboard were concerned only with a decidedly finite problem, and not with anything like Gödel’s theorem, which concerned the infinite variety of the theory of numbers. But the analogy with the formalist conception of mathematics, in which implications were to be followed through mechanically, was still a striking one.

Alan was able to embody this idea in the design of a new form of Bombe at the beginning of 1940. Practical construction began, and was pursued with a speed inconceivable in peacetime, under the direction of Harold ‘Doc’ Keen at the British Tabulating Machinery factory at Letchworth. Here they were used to building office calculators and sorters in which relays performed simple logical functions such as adding and recognising. It was now their task to make relays perform the switching job required for the Bombe to ‘recognise’ the positions in which consistency appeared, and stop. Here again, Alan was the right person to see what was needed, for his unusual experience with the relay multiplier had given him insight into the problems of embodying logical manipulations in this kind of machinery. Perhaps no one, in 1940, was better placed to oversee such work than he.

Yet Alan had not seen
that a dramatic improvement could be made to his design. Here it was Gordon Welchman who played the vital part. He had moved into the Enigma cryptanalytic group with a remarkable achievement to his credit: he had re-invented the perforated sheets method by himself, entirely ignorant of the fact that the Poles had worked it out and that Jeffries already had the production in hand. Then, on studying the Turing Bombe design, he saw that it had failed to exploit Enigma weakness to the full.

Returning to the illustration of the Turing Bombe, we notice that there are other implications which were not followed up, as indicated by the heavier lines:

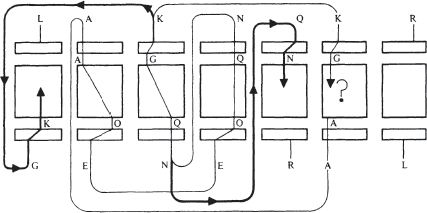
These differ in being implications that could not be foreseen in advance. They arise because (KG) also means (GK), and so at position 1 has an implication for L. Similarly (NQ) also means (QN) and hence at position 5 has an implication by R. This will give rise to a further implication for L at position 7. Clearly there is the possibility of a contradiction arising between these further implications, over and above the question of the loop closing at position 6. Indeed it is not now necessary for the texts to exhibit a loop for a contradiction to arise in this more general way. But this greater power of deduction does depend upon having some automatic means of going from (KG) to (GK), and similarly for every other implication reached, without knowing in advance when or where this may be required.

Welchman not only saw the possibility of improvement, but quickly solved the problem of how to incorporate the further implications into a mechanical process. It required only a simple piece of electrical circuitry – soon to be called the ‘diagonal board’. The name referred to its array of 676 electrical terminals in a 26 × 26 square, each corresponding to an assertion such as (KG), and with wires attached diagonally in such a way that (KG)
was permanently connected to (GK). The diagonal board could be attached to the Bombe in such a way that it had precisely the required effect. No switching operations were required for this; the following of implications could still be achieved by the virtually instantaneous flow of electricity into a connected circuit.

Welchman could hardly believe that he had solved the problem, but drew a rough wiring diagram and convinced himself that it would work. Hurrying to the Cottage, he showed it to Alan, who was also incredulous at first, but rapidly became equally excited about the possibilities it opened up. It was a spectacular improvement; they no longer needed to look for loops, and so could make do with fewer and shorter ‘cribs’.