Zero (4 page)
Authors: Charles Seife

The Fearsome Properties of Nothing
In earliest times did Ymir live: was nor sea nor land nor salty waves, neither earth was there nor upper heaven, but a gaping nothing, and green things nowhere.
âT
HE
E
LDER
E
DDA
It is hard to imagine being afraid of a number. Yet zero was inexorably linked with the voidâwith nothing. There was a primal fear of void and chaos. There was also a fear of zero.
Most ancient peoples believed that only emptiness and chaos were present before the universe came to be. The Greeks claimed that at first Darkness was the mother of all things, and from Darkness sprang Chaos. Darkness and Chaos then spawned the rest of creation. The Hebrew creation myths say that the earth was chaotic and void before God showered it with light and formed its features. (The Hebrew phrase is
tohu v'bohu.
Robert Graves linked these
tohu
to Tehomot, a primal Semitic dragon that was present at the birth of the universe and whose body became the sky and earth.
Bohu
was linked to Behomot, the famed Behemoth monster of Hebrew legend.) The older Hindu tradition tells of a creator who churns the butter of chaos into the earth, and the Norse myth tells a tale of an open void that gets covered with ice, and from the chaos caused by the mingling of fire and ice was born the primal Giant. Emptiness and disorder were the primeval, natural state of the cosmos, and there was always a nagging fear that at the end of time, disorder and void would reign once more. Zero represented that void.
But the fear of zero went deeper than unease about the void. To the ancients, zero's mathematical properties were inexplicable, as shrouded in mystery as the birth of the universe. This is because zero is different from the other numbers. Unlike the other digits in the Babylonian system, zero never was allowed to stand aloneâfor good reason. A lone zero always misbehaves. At the very least it does not behave the way other numbers do.
Add a number to itself and it changes. One and one is not oneâit's two. Two and two is four. But zero and zero is zero. This violates a basic principle of numbers called the axiom of Archimedes, which says that if you add something to itself enough times, it will exceed any other number in magnitude. (The axiom of Archimedes was phrased in terms of areas; a number was viewed as the difference of two unequal areas.) Zero refuses to get bigger. It also refuses to make any other number bigger. Add two and zero and you get two; it is as if you never bothered to add the numbers in the first place. The same thing happens with subtraction. Take zero away from two and you get two. Zero has no substance. Yet this substanceless number threatens to undermine the simplest operations in mathematics, like multiplication and division.
In the realm of numbers, multiplication is a stretchâliterally. Imagine that the number line is a rubber band with tick marks on it (Figure 4). Multiplying by two can be thought of as stretching out the rubber band by a factor of two: the tick mark that was at one is now at two; the tick mark that was at three is now at six. Likewise, multiplying by one-half is like relaxing the rubber band a bit: the tick mark at two is now at one, and the tick mark at three winds up at one and a half. But what happens when you multiply by zero?
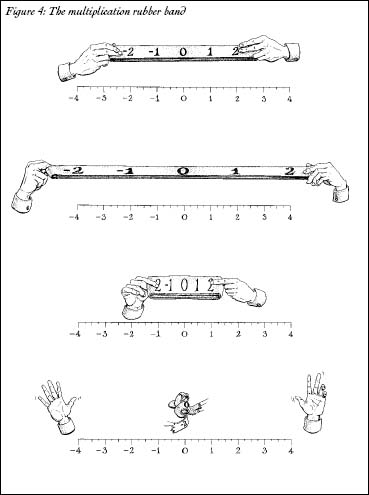
Figure 4: The multiplication rubber band
Anything times zero is zero, so all the tick marks are at zero.
The rubber band has broken. The whole number line has collapsed.
Unfortunately, there is no way to get around this unpleasant fact. Zero times anything must be zero; it's a property of our number system. For everyday numbers to make sense, they have to have something called the
distributive property,
which is best seen through an example. Imagine that a toy store sells balls in groups of two and blocks in groups of three. The neighboring toy store sells a combination pack with two balls and three blocks in it. One bag of balls and one bag of blocks is the same thing as one combination package from the neighboring store. To be consistent, buying seven bags of balls and seven bags of blocks from one toy store has to be the same thing as buying seven combination packs from the neighboring shop. This is the distributive property. Mathematically speaking, we say that 7 Ã 2 + 7 Ã 3 = 7 Ã (2 + 3). Everything comes out right.
Apply this property to zero and something strange happens. We know that 0 + 0 = 0, so a number multiplied by zero is the same thing as multiplying by (0 + 0). Taking two as an example, 2 Ã 0 = 2 Ã (0 + 0), but by the distributive property we know that 2 Ã (0 + 0) is the same thing as 2 Ã 0 + 2 Ã 0. But this means 2 Ã 0 = 2 Ã 0 + 2 Ã 0. Whatever 2 Ã 0 is, when you add it to itself, it stays the same. This seems a lot like zero. In fact, that is just what it is. Subtract 2 Ã 0 from each side of the equation and we see that 0 = 2 Ã 0. Thus, no matter what you do, multiplying a number by zero gives you zero. This troublesome number crushes the number line into a point. But as annoying as this property was, the true power of zero becomes apparent with division, not multiplication.
Just as multiplying by a number stretches the number line, dividing shrinks it. Multiply by two and you stretch the number line by a factor of two; divide by two and you relax the rubber band by a factor of two, undoing the multiplication. Divide by a number and you undo the multiplication: a tick mark that had been stretched to a new place on the number line resumes its original position.
We saw what happened when you multiply a number by zero: the number line is destroyed. Division by zero should be the opposite of multiplying by zero. It should undo the destruction of the number line. Unfortunately, this isn't quite what happens.
In the previous example we saw that 2 Ã 0 is 0. Thus to undo the multiplication, we have to assume that (2 Ã 0)/0 will get us back to 2. Likewise, (3 Ã 0)/0 should get us back to 3, and (4 Ã 0)/0 should equal 4. But 2 Ã 0 and 3 Ã 0 and 4 Ã 0 each equal zero, as we sawâso (2 Ã 0)/0 equals 0/0, as do (3 Ã 0)/0 and (4 Ã 0)/0. Alas, this means that 0/0 equals 2, but it also equals 3, and it also equals 4. This just doesn't make any sense.
Strange things also happen when we look at 1/0 in a different way. Multiplication by zero should undo division by zero, so 1/0 Ã 0 should equal 1. However, we saw that anything multiplied by zero equals zero! There is no such number that, when multiplied by zero, yields oneâat least no number that we've met.
Worst of all, if you wantonly divide by zero, you can destroy the entire foundation of logic and mathematics. Dividing by zero onceâjust one timeâallows you to prove, mathematically, anything at all in the universe. You can prove that 1 + 1 = 42, and from there you can prove that J. Edgar Hoover was a space alien, that William Shakespeare came from Uzbekistan, or even that the sky is polka-dotted. (See appendix A for a proof that Winston Churchill was a carrot.)
Multiplying by zero collapses the number line. But dividing by zero destroys the entire framework of mathematics.
There is a lot of power in this simple number. It was to become the most important tool in mathematics. But thanks to the odd mathematical and philosophical properties of zero, it would clash with the fundamental philosophy of the West.
2
Nothing Comes of Nothing
[ THE WEST REJECTS ZERO ]
Nothing can be created from nothing.
âL
UCRETIUS
,
D
E
R
ERUM
N
ATURA
Z
ero clashed with one of the central tenets of Western philosophy, a dictum whose roots were in the number-philosophy of Pythagoras and whose importance came from the paradoxes of Zeno. The whole Greek universe rested upon this pillar: there is no void.
The Greek universe, created by Pythagoras, Aristotle, and Ptolemy, survived long after the collapse of Greek civilization. In that universe there is no such thing as nothing. There is no zero. Because of this, the West could not accept zero for nearly two millennia. The consequences were dire. Zero's absence would stunt the growth of mathematics, stifle innovation in science, and, incidentally, make a mess of the calendar. Before they could accept zero, philosophers in the West would have to destroy their universe.
The Origin of Greek Number-Philosophy
In the beginning, there was the ratio, and the ratio was with God, and the ratio was God.
*
âJ
OHN 1:1
The Egyptians, who had invented geometry, thought little about mathematics. For them it was a tool to reckon the passage of the days and to maintain plots of land. The Greeks had a very different attitude. To them, numbers and philosophy were inseparable, and they took both very seriously. Indeed, the Greeks went overboard when it came to numbers. Literally.
Hippasus of Metapontum stood on the deck, preparing to die. Around him stood the members of a cult, a secret brotherhood that he had betrayed. Hippasus had revealed a secret that was deadly to the Greek way of thinking, a secret that threatened to undermine the entire philosophy that the brotherhood had struggled to build. For revealing that secret, the great Pythagoras himself sentenced Hippasus to death by drowning. To protect their number-philosophy, the cult would kill. Yet as deadly as the secret that Hippasus revealed was, it was small compared to the dangers of zero.
The leader of the cult was Pythagoras, an ancient radical. According to most accounts, he was born in the sixth century
BC
on Samos, a Greek island off the coast of Turkey famed for a temple to Hera and for really good wine. Even by the standards of the superstitious ancient Greeks, Pythagoras's beliefs were eccentric. He was firmly convinced that he was the reincarnated soul of Euphorbus, a Trojan hero. This helped convince Pythagoras that all soulsâincluding those of animalsâtransmigrated to other bodies after death. Because of this, he was a strict vegetarian. Beans, however, were taboo, as they generate flatulence and are like the genitalia.
Pythagoras may have been an ancient New Age thinker, but he was a powerful orator, a renowned scholar, and a charismatic teacher. He was said to have written the constitution for Greeks living in Italy. Students flocked to him, and he soon acquired a retinue of followers who wanted to learn from the master.
The Pythagoreans lived according to the dicta of their leader. Among other things they believed that it is best to make love to women in the winter, but not in the summer; that all disease is caused by indigestion; that one should eat raw food and drink only water; and that one must avoid wearing wool. But at the center of their philosophy was the most important tenet of the Pythagoreans: all is number.
The Greeks had inherited their numbers from the geometric Egyptians. As a result, in Greek mathematics there was no significant distinction between shapes and numbers. To the Greek philosopher-mathematicians they were pretty much the same thing. (Even today, we have
square
numbers and
triangular
numbers thanks to their influence [Figure 5].) In those days, proving a mathematical theorem was often as simple as drawing an elegant picture; the tools of ancient Greek mathematics weren't pencil and paperâthey were a straightedge and compasses. And to Pythagoras the connection between shapes and numbers was deep and mystical. Every number-shape had a hidden meaning, and the most beautiful number-shapes were sacred.
The mystical symbol of the Pythagorean cult was, naturally, a number-shape: the pentagram, a five-pointed star. This simple figure is a glimpse at the infinite. Nestled within the lines of the star is a pentagon. Connecting the corners of that pentagon with lines generates a small, upside-down, five-pointed star, which is exactly the same as the original star in its proportions. This star, in turn, contains an even smaller pentagon, which contains a tinier star with its tiny pentagon, and so forth (Figure 6). As interesting as this was, to the Pythagoreans the most important property of the pentagram was not in this self-replication but was hidden within the lines of the star. They contained a number-shape that was the ultimate symbol of the Pythagorean view of the universe: the golden ratio.
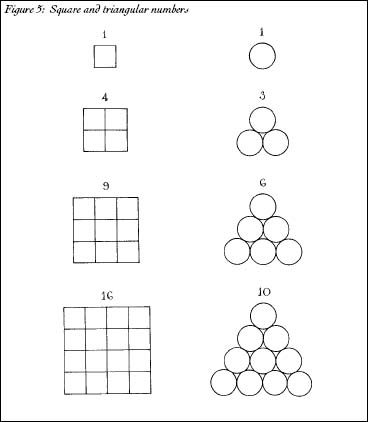
Figure 5: Square and triangular numbers
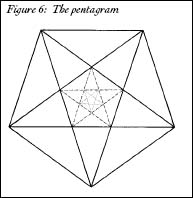
Figure 6: The pentagram
The importance of the golden ratio comes from a Pythagorean discovery that is now barely remembered. In modern schools, children learn of Pythagoras for his famed theorem: the square of the hypotenuse of a right triangle is equal to the sum of the squares of the other two sides. However, this was in fact ancient news. It was known more than 1,000 years before Pythagoras's time. In ancient Greece, Pythagoras was remembered for a different invention: the musical scale.
One day, according to legend, Pythagoras was toying with a monochord, a box with a string on it (Figure 7). By moving a sliding bridge up and down the monochord, Pythagoras changed the notes that the device played. He quickly discovered that strings have a peculiar, yet predictable, behavior. When you pluck the string without the bridge, you get a clear note, the tone known as the
fundamental.
Putting the bridge on the monochord so it touches the string changes the notes that are played. When you place the bridge exactly in the middle of the monochord, touching the center of the string, each half of the string plays the same note: a tone exactly one octave higher than the string's fundamental. Shifting the bridge slightly might divide the string so that one side has three-fifths of the string and the other has two-fifths; in this case Pythagoras noticed that plucking the string segments creates two notes that form a
perfect fifth,
which is said to be the most powerful and evocative musical relationship. Different ratios gave different tones that could soothe or disturb. (The discordant tritone, for instance, was dubbed the “devil in music” and was rejected by medieval musicians.) Oddly enough, when Pythagoras put the bridge at a place that did not divide the string into a simple ratio, the plucked notes did not meld well. The sound was usually dissonant and sometimes even worse. Often the tone wobbled like a drunkard up and down the scale.
To Pythagoras, playing music was a mathematical act. Like squares and triangles, lines were number-shapes, so dividing a string into two parts was the same as taking a ratio of two numbers. The harmony of the monochord was the harmony of mathematicsâand the harmony of the universe. Pythagoras concluded that ratios govern not only music but also all other types of beauty. To the Pythagoreans, ratios and proportions controlled musical beauty, physical beauty, and mathematical beauty. Understanding nature was as simple as understanding the mathematics of proportions.
Figure 7: The mystical monochord
This philosophyâthe interchangeability of music, math, and natureâled to the earliest Pythagorean model of the planets. Pythagoras argued that the earth sat at the center of the universe, and the sun, moon, planets, and stars revolved around the earth, each pinned inside a sphere (Figure 8). The ratios of the sizes of the spheres were nice and orderly, and as the spheres moved, they made music. The outermost planets, Jupiter and Saturn, moved the fastest and made the highest-pitched notes. The innermost ones, like the moon, made lower notes. Taken all together, the moving planets made a “harmony of the spheres,” and the heavens are a beautiful mathematical orchestra. This is what Pythagoras meant when he insisted, “All is number.”
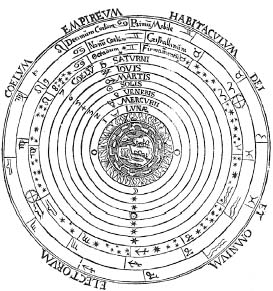
Figure 8: The Greek universe
Because ratios were the keys to understanding nature, the Pythagoreans and later Greek mathematicians spent much of their energy investigating their properties. Eventually, they categorized proportions into 10 different classes, with names like the
harmonic mean.
One of these means yielded the most “beautiful” number in the world: the golden ratio.
Achieving this blissful mean is a matter of dividing a line in a special way: divide it in two so that the ratio of the small part to the large part is the same as the ratio of the large part to the whole (see appendix B). In words, it doesn't seem particularly special, but figures imbued with this golden ratio seem to be the most beautiful objects. Even today, artists and architects intuitively know that objects that have this ratio of length to width are the most aesthetically pleasing, and the ratio governs the proportions of many works of art and architecture. Some historians and mathematicians argue that the Parthenon, the majestic Athenian temple, was built so that the golden ratio is visible in every aspect of its construction. Even nature seems to have the golden ratio in its design plans. Compare the ratios of the size of any two succeeding chambers of the nautilus, or take the ratio of clockwise grooves to counterclockwise grooves in the pineapple, and you will see that these ratios approach the golden ratio (Figure 9).
The pentagram became the most sacred symbol of the Pythagorean brotherhood because the lines of the star are divided in this special wayâthe pentagram is chock-full of the golden ratioâand for Pythagoras, the golden ratio was the king of numbers. The golden ratio was favored by artists and nature alike and seemed to prove the Pythagorean assertion that music, beauty, architecture, nature, and the very construction of the cosmos were all intertwined and inseparable. To the Pythagorean mind, ratios controlled the universe, and what was true for the Pythagoreans soon became true for the entire West. The supernatural link between aesthetics, ratios, and the universe became one of the central and long-lasting tenets of Western civilization. As late as Shakespeare's time, scientists talked about the revolution of orbs of different proportions and discussed the heavenly music that reverberated throughout the cosmos.