Zero (3 page)

Zero was the solution to the problem. By around 300
BC
the Babylonians had started using two slanted wedges,
, to represent an empty space, an empty column on the abacus. This
placeholder
mark made it easy to tell which position a symbol was in. Before the advent of zero,
could be interpreted as 61 or 3,601. But with zero,
meant 61; 3,601 was written as
(Figure 2). Zero was born out of the need to give any given sequence of Babylonian digits a unique, permanent meaning.

Though zero was useful, it was only a placeholder. It was merely a symbol for a blank place in the abacus, a column where all the stones were at the bottom. It did little more than make sure digits fell in the right places; it didn't really have a numerical value of its own. After all, 000,002,148 means exactly the same thing as 2,148. A zero in a string of digits takes its meaning from some other digit to its left. On its own, it meant…nothing. Zero was a digit, not a number. It had no value.

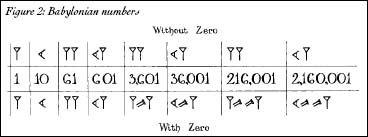
Figure 2: Babylonian numbers

A number's value comes from its place on the number line—from its position compared with other numbers. For instance, the number two comes before the number three and after the number one; nowhere else makes any sense. However, the 0 mark didn't have a spot on the number line at first. It was just a symbol; it didn't have a place in the hierarchy of numbers. Even today, we sometimes treat zero as a nonnumber even though we all know that zero has a numerical value of its own, using the digit 0 as a placeholder without connecting it to the number zero. Look at a telephone or the top of a computer keyboard. The 0 comes after the 9, not before the 1 where it belongs. It doesn't matter where the placeholder 0 sits; it can be anywhere in the number sequence. But nowadays everybody knows that zero can't really sit anywhere on the number line, because it has a definite numerical value of its own. It is the number that separates the positive numbers from the negative numbers. It is an even number, and it is the integer that precedes one. Zero must sit in its rightful place on the number line, before one and after negative one. Nowhere else makes any sense. Yet zero sits at the end of the computer and at the bottom of the telephone because we always start counting with one.

One seems like the appropriate place to start counting, but doing so forces us to put zero in an unnatural place. To other cultures, like the Mayan people of Mexico and Central America, starting with one didn't seem like the rational thing to do. In fact, the Mayans had a number system—and a calendar—that made more sense than ours does. Like the Babylonians, the Mayans had a
place-value
system of digits and places. The only real difference was that instead of basing their numbers on 60 as the Babylonians did, the Mayans had a vigesimal, base-20 system that had the remnants of an earlier base-10 system in it. And like the Babylonians, they needed a zero to keep track of what each digit meant. Just to make things interesting, the Mayans had two types of digits. The simple type was based on dots and lines, while the complicated type was based on glyphs—grotesque faces. To a modern eye, Mayan glyph writing is about as alien-looking as you can get (Figure 3).

Like the Egyptians, the Mayans also had an excellent solar calendar. Because their system of counting was based on the number 20, the Mayans naturally divided their year into 18 months of 20 days each, totaling 360 days. A special period of five days at the end, called Uayeb, brought the count to 365. Unlike the Egyptians, though, the Mayans had a zero in their counting system, so they did the obvious thing: they started numbering days with the number zero. The first day of the month of Zip, for example, was usually called the “installation” or “seating” of Zip. The next day was 1 Zip, the following day was 2 Zip, and so forth, until they reached 19 Zip. The next day was the seating of Zotz'—0 Zotz' followed by 1 Zotz' and so forth. Each month had 20 days, numbered 0 through 19, not numbered 1 through 20 as we do today. (The Mayan calendar was wonderfully complicated. Along with this solar calendar, there was a ritual calendar that had 20 weeks, each of 13 days. Combined with the solar year, this created a
calendar round
that had a different name for every day in a 52-year cycle.)

Figure 3: Mayan numbers

The Mayan system made more sense than the Western system does. Since the Western calendar was created at a time when there was no zero, we never see a day zero, or a year zero. This apparently insignificant omission caused a great deal of trouble; it kindled the controversy over the start of the millennium. The Mayans would never have argued about whether 2000 or 2001 was the first year in the twenty-first century. But it was not the Mayans who formed our calendar; it was the Egyptians and, later, the Romans. For this reason, we are stuck with a troublesome, zero-free calendar.

The Egyptian civilization's lack of zero was bad for the calendar and bad for the future of Western mathematics. In fact, Egyptian civilization was bad for math in more ways than one; it was not just the absence of a zero that caused future difficulties. The Egyptians had an extremely cumbersome way of handling fractions. They didn't think of ¾ as a ratio of three to four as we do today; they saw it as the sum of ½ and ¼. With the sole exception of
²
/
₃
, all Egyptian fractions were written as a sum of numbers in the form of 1/
n
(where
n
is a counting number)—the so-called unit fractions. Long chains of these unit fractions made ratios extremely difficult to handle in the Egyptian (and Greek) number systems.

Zero makes this cumbersome system obsolete. In the Babylonian system—with zero in it—it's easy to write fractions. Just as we can write 0.5 for ½ and 0.75 for ¾, the Babylonians used the numbers 0;30 for ½ and 0;45 for ¾. (In fact, the Babylonian base-60 system is even better suited to writing down fractions than our modern-day base-10 system.)

Unfortunately, the Greeks and Romans hated zero so much that they clung to their own Egyptian-like notation rather than convert to the Babylonian system, even though the Babylonian system was easier to use. For intricate calculations, like those needed to create astronomical tables, the Greek system was so cumbersome that the mathematicians converted the unit fractions to the Babylonian sexagesimal system, did the calculations, and then translated the answers back into the Greek style. They could have saved many time-consuming steps. (We all know how fun it is to convert fractions back and forth!) However, the Greeks so despised zero that they refused to admit it into their writings, even though they saw how useful it was. The reason: zero was dangerous.