Warped Passages (65 page)

That is a stupendous difference. For three-quarters of a century after Theodor Kaluza introduced the idea of an extra dimension of space in 1919, physicists believed that extra dimensions were acceptable, but only if they were finite in size, either curled up or bounded between branes. Infinite extra dimensions were supposed to be very easy to rule out because the gravitational force, which would spread infinitely far in these dimensions, would look wrong at all distance scales, even those that we know about already. An infinite fifth dimension was supposed to destabilize everything around us, even the solar system, which is held together by Newtonian physics.
This chapter explains why this reasoning is not always correct.
We’ll investigate an entirely new reason why extra dimensions might be hidden, which Raman and I discovered in 1999. Spacetime can be so warped that the gravitational field becomes highly concentrated in a small region near a brane—so concentrated that the huge expanse of an infinite dimension is inconsequential. The gravitational force is not lost into the extra dimensions, but remains focused in a small region near a brane.
Figure 86.
Infinite warped spacetime with a single brane. There is a single four-dimensional brane in a five-dimensional universe. The Standard Model resides on this single brane.
In this scenario, the graviton, the particle that communicates gravity, is
localized
near a brane, which is the Brane of Athena’s story, but which I’ll call the Gravitybrane from now on. Athena’s dream took her to this warped five-dimensional space, in which the Gravitybrane so radically alters the nature of spacetime that space appears to be four-dimensional, even though it is in reality five-dimensional. Remarkably, a warped higher dimension can have infinite extent, yet nonetheless be hidden, while the three flat infinite dimensions reproduce the physics of our world.
The Localized Graviton
You might recall that when I first introduced branes, I distinguished reluctance to explore distant regions from genuine confinement, which explicitly forbids foreign travel beyond the place where someone or something is confined. Although you’ve probably never visited Greenland, no law forbids you from going there. But some places are just too much trouble to get to. Even if travel to such places is permitted, and even if they are no further away than some other places you’ve been, you still might just never go there.
Or imagine someone who has broken his leg. In principle, he could leave the house whenever he likes, but he’s much more likely to be found inside the house than outside, even when no bars or locks are keeping him there.
Similarly, the localized graviton has unrestricted access to an infinite fifth dimension. But it is nonetheless highly concentrated in the vicinity of a brane, and has very low probability of being found far away. According to general relativity, everything—including the graviton—is subject to the gravitational force. The graviton is not at all impaired, but it behaves as if it is gravitationally attracted to the brane and therefore remains close by. And because the graviton only rarely travels outside a limited region, the extra dimension can be infinite without giving rise to any dangerous effects that would rule the theory out.
In our work, Raman and I concentrated on gravity in a five-dimensional spacetime with only a single extra dimension of space. We could thereby concentrate on the localization mechanism we are about to discuss, which keeps gravity in a small region of the five-dimensional spacetime. I’ll assume that if the universe has ten or more dimensions, some mixture of localization and curling them up hides the rest. Such additional hidden dimensions wouldn’t affect the localization phenomenon I’m about to describe, so we’ll ignore them and focus on the five dimensions that are critical to our discussion.
In our model a single brane sits at one end of the fifth spacetime dimension. It is reflective, as were the two branes I described in
Chapter 20. Things that hit the brane simply bounce back, so nothing loses energy when it hits this brane. Because the model we are now considering contains only this single brane, we’ll assume that the Standard Model particles are confined there; note the distinction from the model I discussed in the previous chapter, in which the Standard Model particles were on the Weakbrane, which no longer exists. The location of the Standard Model particles is not relevant to the spacetime geometry, but it does of course have implications for particle physics.
Although in this chapter we are interested in the single-brane theory, the first clue Raman and I had that an infinite fifth dimension might be legitimate was a curious feature of the warped geometry with two branes. We initially assumed that the second brane served two functions. One was to confine the Standard Model particles; the second was to make the fifth dimension finite. As with flat extra dimensions, a finite fifth dimension guaranteed that at sufficiently large distance, gravity would be that of four-dimensional spacetime.
However, a peculiar fact suggested that this latter role for the second brane was a red herring, and that the second brane was not essential for gravity to mimic that of a genuinely four-dimensional universe: the four-dimensional graviton’s interactions were virtually independent of the fifth dimension’s size. A calculation showed that gravity would have the same strength if the second brane stayed where it was, or if it were twice as far from the Gravitybrane, or if it were ten times as far out into the bulk, further away from the first brane. In fact, four-dimensional gravity persisted even if our model put the second brane at infinity—which is to say, eliminated it altogether. This should not be true if the second brane and a finite dimension were essential for reproducing four-dimensional gravity.
This was our first clue that the intuition that we need a second brane was based on flat dimensions and wasn’t necessarily true for warped spacetime. With a flat extra dimension, the second brane is compulsory for four-dimensional gravity. We can see this with the aid of the sprinkler analogy from Chapter 20. A flat extra dimension would correspond to water being distributed equally everywhere along
a long straight sprinkler (see Figure 81, Chapter 20).
*
The longer the sprinkler, the less water would be sprinkled on any given garden. If we were to extend this reasoning to an infinitely long sprinkler, we would see that the water would be spread so thinly that essentially no water would be sprinkled on any finite-sized garden.
Similarly, if gravity were spread throughout an infinite uniform dimension, the gravitational force would be so attenuated along the extra dimension that it would be reduced to nothing. A geometry with an infinite extra dimension would have to contain some subtlety that goes beyond this simple intuitive picture if gravity is to behave four-dimensionally. And indeed, warped spacetime provides the requisite added ingredient.
To see how this works, let’s once again use our sprinkler analogy to identify the loophole in the argument above. Suppose that you have an infinitely long sprinkler, but you don’t distribute water equally everywhere. Instead, you have control over how the water is allocated, giving you the option of ensuring that your own garden is well watered. One way of accomplishing this would be to deliver half the water to your plot of land and the remaining half of the water everywhere else. In that case, although the gardens far away would be badly treated, your garden would be guaranteed to receive all the water it needs. Your garden would always receive half the water, even though the sprinkler continues delivering water indefinitely far away. With an inequitable distribution of water, you would get all the water you need. The sprinkler could be infinite but you wouldn’t know the distance.
Similarly, the graviton’s probability function in our warped geometry is always very big near the Gravitybrane, despite the infinite fifth dimension. As in the previous chapter, the probability function for the graviton peaks on this brane (see Figure 87), and falls off exponentially as the graviton moves away from the Gravitybrane into the fifth dimension. In this theory, however, the graviton’s probability function continues indefinitely far but it is inconsequential to the size of the graviton probability function near the brane.
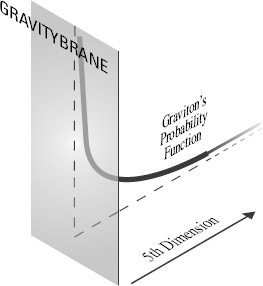
Figure 87.
The graviton’s probability function in infinite warped spacetime with a single brane.
A plummeting probability function of this sort tells us that the likelihood of finding the graviton far from the Gravitybrane is extremely tiny—so tiny that we can generally ignore the distant regions of the fifth dimension. Although in principle the graviton can be anywhere along the fifth dimension, the exponential decrease makes the graviton’s probability function very concentrated in the vicinity of the Gravitybrane. The situation is almost, but not quite, as if a second brane confined the graviton to a limited region.
The high probability for the graviton to be found near the Gravitybrane, and the corresponding concentration of the gravitational field there, might also be compared to the high likelihood of greedy ducks in a pond being near the shore. Usually the ducks aren’t equally spaced across the pond, but instead congregate near breadcrumbs that bird lovers have tossed in (see Figure 88). So the size of the pond would be essentially immaterial to the distribution of ducks. Similarly, in warped spacetime, gravity attracts the graviton to the Gravitybrane, so the extent of the fifth dimension is irrelevant.
You can also see why the fifth dimension doesn’t affect gravity very much by considering the gravitational field surrounding an object on the Gravitybrane. We have seen that in flat spatial dimensions, the force lines emanating from an object spread equally in all directions. And when there were finite extra dimensions, the field lines extended
in all directions until some reached a boundary and bent around. For this reason, gravitational field lines that are further from an object than the size of the extra dimensions spread only along the three infinite dimensions of the lower-dimensional world.
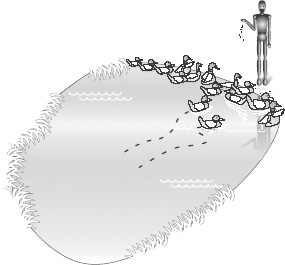
Figure 88.
If ducks are concentrated near the shore, you can count almost all of them by counting the ones nearby.
In the warped scenario, on the other hand, field lines do not distribute themselves equally in all directions; it’s only along the brane that they extend equally in all directions. Perpendicular to the brane, they extend very little (see Figure 89). Because the gravitational field lines spread out primarily along the brane, the gravitational field looks almost identical to the field associated with an object in four dimensions. The spread into the fifth dimension is so small (not much more than the Planck scale length, 10
-33
cm) that we can ignore it. Although the extra dimension is infinite, it is irrelevant to the gravitational field of a brane-bound object.
You can also see how Raman and I resolved the initial puzzle we faced: why the size of the fifth dimension is irrelevant to the strength of gravity. Returning to the sprinkler analogy above, suppose we now specify the distribution of water over the entire sprinkler, so that it resembles the distribution of gravity from the plummeting graviton’s probability function: after you take half of the water for your garden, you then send half of the remaining water to the adjacent garden, half
of that amount to the next one, and so on, with everyone in successive gardens receiving half as much water as their neighbor. To mimic a second brane in the fifth dimension, we’ll assume that we stop delivering water beyond a certain point, just as a second brane in the fifth dimension would cut off the graviton’s probability function at some point along the fifth dimension. And to mimic an infinite fifth dimension, we’ll assume that the water delivers water indefinitely along its length.