Understanding Sabermetrics (2 page)
Read Understanding Sabermetrics Online
Authors: Gabriel B. Costa,Michael R. Huber,John T. Saccoma

We also provide what we have termed an “educational module” in an appendix. Because this book can be used as a text for a course in sabermetrics, the module can serve as a primer for the instructor and the student. We three authors have taught courses on sabermetrics, individually or with colleagues, dozens of times, ranging over a period of nearly two decades. This appendix covers such topics as course prerequisites, objectives, content, and assessment tools. It is our hope that this feature will prove helpful and encourage other institutions to offer a course on sabermetrics.
I would like to thank my Archbishop, Most Reverend John J. Myers. In every sense, his guidance and support have been a blessing.
From Seton Hall University, I am grateful to the Priest Community, ministered to by Monsignor James M. Cafone, to my colleagues in the Department of Mathematics and Computer Science, chaired by Dr. Joan Guetti, and to Dean Joseph Marbach and Associate Dean Parviz Ansari of the College of Arts and Sciences. Thank you from the bottom of my heart.
Lastly, to Colonel Michael Phillips and the entire Department of Mathematical Sciences at the United States Military Academy, thank you for your friendship and support.
MICHAEL R. HUBER: In addition to thanking my coauthors, I would like to thank my colleagues at the United States Military Academy who assisted us in our sabermetrics course: Jeff Broadwater, Scott Billie, Alex Heidenberg, Mike Phillips, Andy Glen, and Rod Sturdivant. I want to thank Gabriel Schechter and Jim Gates of the National Baseball Hall of Fame and Museum, for always welcoming our classes and devoting their precious time to teaching our students about sabermetrics.
JOHN T. SACCOMAN: I would like to thank my coauthors, who are equally mathematicians and baseball men, not mere dabblers in either. Baseball and mathematics are our avocations, and it is a rare pleasure to find such kindred spirits.
Pre-Game : Abbreviations and Formulas
G = Games played
AB = At-bats
H = Hits
BB = Bases on balls (Walks)
IBB = Intentional bases on balls
HP = Hit by pitch
R = Runs scored
RBI = Runs batted in
1B = Singles
2B = Doubles
3B = Triples
HR = Home runs
BA = Batting Average = H / AB
OBA = On-base average = (H + BB + HP) / (AB + BB + HP)
TB = Total bases = 1(1B) + 2(2B) + 3(3B) + 4(HR)
SLG = Slugging average = TB / AB
OPS = On-base plus slugging = OBA + SLG
ISO = Isolated power = SLG - BA = (TB - H) / AB
TPQ = Total power quotient = (HR + RBI + TB) / AB
PwrF = Power factor = SLG/BA = TB/H
SF = Sacrifice flies
SH = Sacrifice hits (Bunts)
Base RunningSB = Stolen bases
CS = Caught stealing
OOB = Outs on base
PitchingW = Wins
L = Losses
PCT = Winning percentage = W / (W + L)
ER = Earned Runs allowed
IP = Innings pitched
ERA = Earned run average = 9 × ER / IP
SV = Saves
K = Strikeouts
BB = Bases on balls (allowed)
FieldingA = Assists
E = Errors
PO = Putouts
FLD = Fielding average = (A + PO) / (A + PO + E)
RF = Range factor (per game) = (A + PO) / G
Batting Practice: Introduction and Statistics
Numbers have always played a major role in baseball and its fans’ love for the game. How many people can explain the significance of these numbers: 511; 73; 714; 56; .406; 4256?
Respectively, they represent Cy Young’s career wins total; Barry Bonds’s 2001 home run total; Babe Ruth’s career home run total; the length in games of Joe DiMaggio’s 1941 hitting streak; Ted Williams’s 1941 batting average; Pete Rose’s career hits total.
What is sabermetrics? The term is a combination of the acronym SABR (Society of American Baseball Research) and “metrics,” meaning “measurement.” Defined variously as the “search for objective knowledge about baseball” and “the mathematical and statistical analysis of baseball records” by the man who coined the term, noted baseball author Bill James, sabermetrics has become more and more widely accepted as an evaluation tool. Baseball fans, who already memorize and quote numbers to the thousandths place (as in no other part of their lives), now work into their baseball arguments such terms as OPS (on-base plus slugging percentages), its mathematically superior cousin, the SLOB (slugging times on base), WHIP (walks plus hits per inning pitched) and RF (range factor).
James once wrote that the main reason for sabermetrics is that there is a Baseball Hall of Fame, and sabermetrics arguments are frequently used to plead the case for a player’s inclusion in (or exclusion from) the Hall. However, as Michael Lewis’s bestseller
Moneyball
attests, baseball insiders are taking a serious look at sabermetrics as a team-building tool. Just as a study of baseball statistics can help people better understand mathematics,
Moneyball
is viewed in the business community as a model for business startups.
Moneyball
attests, baseball insiders are taking a serious look at sabermetrics as a team-building tool. Just as a study of baseball statistics can help people better understand mathematics,
Moneyball
is viewed in the business community as a model for business startups.
The main contribution of Bill James and Pete Palmer, another noted sabermetrician, is their exposure of the deficiency of looking at merely the traditional statistics. Fresh analysis can be provided by the new statistics, or at the very least, by a new twist on the old statistics.
When doing statistical analyses and data mining, anomalies are bound to appear, and baseball numbers are no stranger to these. For example, when combining unequally sized groups into a larger data set, expectations can be confounded. An example of this is known as Simpson’s Paradox. To illustrate how this can work in baseball, consider the following example. Player A may have a .223 BA against right-handed pitching (45 H / 202 AB) and a .284 BA against lefties (71 H / 250 AB), giving him an overall BA of .257 (116 H / 452 AB). Player B may have a higher BA against righties (.232 on 58 H / 250 AB) and a higher one against lefthanders as well (.296 on 32 H / 108 AB), but his overall batting average can nonetheless be lower than that of player A (.251, or 90 H / 358 AB).
Descriptive statistics provide the mathematical underpinning for many of the measures used in sabermetrics, so it is here that we review some terms and formulas. If you feel comfortable with this subject, you may skip ahead to the next chapter.
Statistics RefresherWe define the
mean
, or average, of a data set to be the sum of the elements in the set divided by the total number of elements in the set. It is a measure of central tendency. Let’s think about the mean by way of an example. The following are the year-by-year home run totals for Hank Aaron over the course of his career: 13 27 26 44 30 39 40 34 45 44 24 32 44 39 29 44 38 47 34 40 20 12 10. The mean of this set is denoted by the symbol
x
 and is determined to be
and is determined to be
x
 = 32.83 (755 total home runs divided by 23 seasons). Another measure of central tendency is the
= 32.83 (755 total home runs divided by 23 seasons). Another measure of central tendency is the
median
, which provides the midpoint of the data set. For Aaron’s home runs, this is 34, i.e., he had as many seasons with more than 34 home runs as he did with fewer. Finally, the
mode
is the most frequently occurring element in the data set. For Aaron’s home runs, this number is 44, which, coincidentally, also happens to be his uniform number. The mode and median are least affected by unusually high or low score, while the mean is most stable, meaning that it shows the least variability when several random samples are taken. In a data set that is normally distributed, one in which the data can be modeled by a bell-shaped curve, all three of the measures are equal. For Aaron, they are not; however, in his playing days, it would be reasonable to expect Hank Aaron to hit 32 to 34 home runs per season based on this data.
mean
, or average, of a data set to be the sum of the elements in the set divided by the total number of elements in the set. It is a measure of central tendency. Let’s think about the mean by way of an example. The following are the year-by-year home run totals for Hank Aaron over the course of his career: 13 27 26 44 30 39 40 34 45 44 24 32 44 39 29 44 38 47 34 40 20 12 10. The mean of this set is denoted by the symbol
x
 and is determined to be
and is determined to bex
 = 32.83 (755 total home runs divided by 23 seasons). Another measure of central tendency is the
= 32.83 (755 total home runs divided by 23 seasons). Another measure of central tendency is themedian
, which provides the midpoint of the data set. For Aaron’s home runs, this is 34, i.e., he had as many seasons with more than 34 home runs as he did with fewer. Finally, the
mode
is the most frequently occurring element in the data set. For Aaron’s home runs, this number is 44, which, coincidentally, also happens to be his uniform number. The mode and median are least affected by unusually high or low score, while the mean is most stable, meaning that it shows the least variability when several random samples are taken. In a data set that is normally distributed, one in which the data can be modeled by a bell-shaped curve, all three of the measures are equal. For Aaron, they are not; however, in his playing days, it would be reasonable to expect Hank Aaron to hit 32 to 34 home runs per season based on this data.
In statistics, measures of dispersion show how tightly spread out the data is in relation to a measure of central tendency. The main measures of the dispersion of the data are range, variance and standard deviation. Aaron’s seasonal home run totals vary from a low of 10 to a high of 47. The
range
is the maximum minus the minimum, so for Aaron, this is 47 minus 10, or 37. If the home run data is broken up into quartiles, we see that the first quartile would be those values less than 26, the second quartile ends at the median (34) and the third quartile ends at 44. Thus, the interquartile range (IQR) is 44 − 26 = 18, meaning that 50 percent of the data is separated by 18.
range
is the maximum minus the minimum, so for Aaron, this is 47 minus 10, or 37. If the home run data is broken up into quartiles, we see that the first quartile would be those values less than 26, the second quartile ends at the median (34) and the third quartile ends at 44. Thus, the interquartile range (IQR) is 44 − 26 = 18, meaning that 50 percent of the data is separated by 18.
A measure of dispersion that utilizes the mean is called the
variance
. Its formula is given by
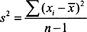 where
where
n
represents the number of items in the data set. Aaron’s season-by-season home run totals have a variance of 119.62. The square root of the variance is the
standard deviation
, and it is this measure that gives a clearer picture of the spread of the data. Aaron’s standard deviation is 10.49, and it can be inferred from Chebyshev’s rule that at least 75 percent of the data falls within two standard deviations of the mean, i.e., between 32.83 and ±(2 × 10.49) or between about 10 and 55, which in fact 100 percent of the values do.
variance
. Its formula is given by
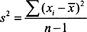
n
represents the number of items in the data set. Aaron’s season-by-season home run totals have a variance of 119.62. The square root of the variance is the
standard deviation
, and it is this measure that gives a clearer picture of the spread of the data. Aaron’s standard deviation is 10.49, and it can be inferred from Chebyshev’s rule that at least 75 percent of the data falls within two standard deviations of the mean, i.e., between 32.83 and ±(2 × 10.49) or between about 10 and 55, which in fact 100 percent of the values do.
The mathematical bases for many of the formulas used in sabermetrics are provided by a study of statistical regression and correlation. These studies attempt to determine a line that nearly approximates data that can be expressed as ordered pairs, and how well-defined this linear relationship is. If the second coordinate increases when the first coordinate does, then the correlation is said to be positive. If the second coordinate decreases when the first increases, the correlation is said to be negative. As an example, we will use a sample of the home run and runs batted in totals for some of the seasons of Gil Hodges’ career. Hodges played 18 seasons in the National League, for the Brooklyn (and later Los Angeles) Dodgers and the New York Mets. Consider the following chart:
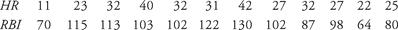
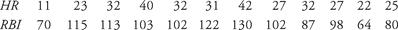
Table 1.1 Gil Hodges’ HR and RBI numbers for 12 years of his career
Other books
Every Happy Family by Dede Crane
The Finding by Jenna Elizabeth Johnson
The Deadsong by Brandon Hardy
Birds in Paradise by Dorothy McFalls
The Monstrous Child by Francesca Simon
The Dark Arts of Blood by Freda Warrington
Calendar Girl by Stella Duffy
Colton's Dilemma (Shadow Breeds) by Nelson, Dara
El caballero de Olmedo by Lope de Vega
The Spirit Gate by Maya Kaathryn Bohnhoff