The Thing with Feathers (18 page)
Read The Thing with Feathers Online
Authors: Noah Strycker

In a sport like tennis, with relatively stable rankings and the purest talent at the top, the round-robin format seems to permit fewer flukes. If a good player has a bad day, he gets a second chance. A quick glance at the list of World Tour Finals champions from the past forty years confirms this idea; Roger Federer has won the event six times, Pete Sampras and Ivan Lendl five times each.
These round-robins can also get confusing, though. In 2006, three players in one of the groups—Andy Roddick, Ivan Ljubicˇic, and David Nalbandian—had each won one match, with a somewhat circular result: Roddick beat Ljubicˇic, who beat Nalbandian, who beat Roddick. The three-way tie was broken by advancing the player who had won the most sets (Nalbandian), but the denouement was unsatisfying.
Though round-robin tournaments may appear to result in true rankings, the reality is that they often don’t.
Things did not go smoothly in 2007, for example, when the men’s professional tennis organization decided to try the round-robin format at several other events. At a Las Vegas tournament that year, American defending champion James Blake was playing Argentinian Juan Martín del Potro for a slot in the quarterfinals when del Potro, who wasn’t feeling well, called it quits halfway through the second set. Blake had built a commanding lead, and, had he finished the match, would have advanced easily. But because the match was stopped, he didn’t qualify for the quarterfinals. Outcry was immediate and
intense. At one point, it was decided that Blake would advance anyway; a day later, the decision was reversed. It was all very embarrassing and confused.
Within a month, the round-robin idea was quietly abandoned, and all regular-season tournaments reverted to single-elimination format. The experiment, though a failure for men’s tennis, did draw attention to a longstanding question in the upper echelon of professional sports: Is there an inherent, absolute skill ladder among the top contenders that holds up under random matchups, or can only a brutal system, like single-elimination draws, yield a decisive list of rankings? The answer, it seems, lies somewhere in the middle.
What does any of this have to do with chickens? A lot, actually. Tennis rankings are a pecking order among athletes based on head-to-head matches. This system—from the World Tour Finals to your backyard chicken coop—is more triangular than you might think.
—
AN IDEAL PECKING ORDER
is perfectly hierarchical, like the rungs of a ladder, with no two subjects of equal rank. This is what’s known mathematically as transitivity: A is greater than B, which is greater than C, and so on down the list. Many things appear to be transitive—pecking orders in chicken coops, professional tennis rankings, even the body weights of ten random people lined up from largest to smallest. But some characteristics lend themselves more to this kind of hierarchy than others. Absolute values, like weight, will always be perfectly transitive. Other things we often think of as absolute—dominance in chicken coops and on tennis courts—aren’t always perfectly measurable.
Some ornithologists have used transitive relationships as a
test of overall intelligence: Can birds infer rankings by applying logic to separate pieces of information? In the most straightforward example, a bird might be repeatedly given a choice between options A and B, and always rewarded for picking A and punished for picking B. Once it has learned to prefer A over B, the bird may be offered a new choice between B and a third option, C, but this time be rewarded for picking B and punished for picking C. In this way, after learning to prefer A over B, the bird will also learn to choose B over C. Then, the interesting part: What would that trained bird do with a novel choice, A vs. C? Will it pick A?
Experiments show that pigeons (and other animals, including monkeys) will generally choose option A, apparently making the mental leap that if A > B and B > C, then A > C. In practice, chickens could use this kind of reasoning to efficiently determine their pecking order. If one bird in the coop dominates another, and that one dominates a third, then the first one wouldn’t have to prove itself against the third. But it’s probably not that easy; this lab test may be too simple to explain what’s really going on. For instance, the trained bird may pick A over C just because it has always been rewarded for picking A and punished for picking C in other pairings.
So the experiment gets more complicated. This time, the bird is trained with five options instead of three, to teach it that A > B, B > C, C > D, and D > E. Once it reliably learns each of these pairings, the bird is given a choice between B and D, each of which was rewarded half the time in training. Pigeons will, in fact, pick B over D, suggesting that they can track a transitive order. But this experiment may also be too simple. The pigeons might pick B just because they’ve often seen it with the dominant A, and they might reject D because it’s often alongside the lowly E. This is the “value transfer” hypothesis, and
you’ve seen it in practice when regular guys join the entourage of rich, Ferrari-driving friends to attract women—they’re hoping women will prefer someone in the passenger seat of a Ferrari over some random guy on the street. Value transfer is real and measurable, but unfortunately it’s practically impossible to devise an experiment complicated enough to rule out the effect—even with seven options, which is the most that a pigeon can usually be trained to separate in its lifetime.
The trouble with these lab tests is that, for a pigeon or a chicken or any other animal, pecking at colored buttons for a superficial reward has no inherent value—the birds have to be painstakingly trained to prefer one button over another strictly for experimental purposes. The pecking order in a chicken coop, on the other hand, has immediate, real rewards and consequences; the birds must quickly learn how to pick their fights or they’ll get beat up.
Real-world evidence does suggest that chickens can use logic to infer their place in the pecking order. When chickens observe an unfamiliar bird facing off with a higher-ranking individual, they are later more likely to pick a fight with the newcomer if it lost. If the new bird beats the existing dominant chicken, others in the coop will usually leave it unchallenged. Nobody has been able to prove that these fight-or-not decisions affect the pecking order itself, so it’s debatable whether chickens use implied logic to construct their hierarchy, but this observation is interesting.
If chickens can really weigh dominance relationships and fill in gaps without having to fight every other bird in the coop, then pecking orders can be seen as an expression of intelligence in a creature not usually known for its mental capacity. That would be pretty cool.
—
TRY THIS PEN-AND-PAPER EXERCISE
to see for yourself how pecking orders work, often imperfectly.
- Draw a large octagon on a sheet of paper.
- Draw a line from every point of the octagon to every other point.
- Think of any eight foods, and label each outside corner with one of them. Your diagram should look like a stop sign inscribed with an eight-pointed star shape, each corner labeled with a food.
- Without thinking too hard, decide which food you like best from each possible pairing. Label each straight line with an arrow pointing toward your preference.
- Count up how many “wins” each of your eight foods received.
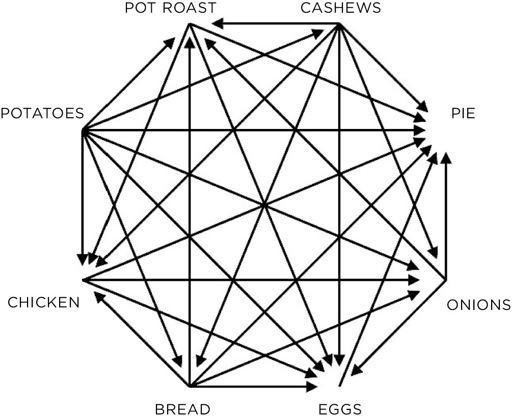
When I tried this exercise with pot roast, cashews, pie, onions, eggs, bread, chicken, and potatoes, I vastly preferred pie (seven votes) to potatoes (zero votes). No surprise there. Cashews and bread had one and two votes, respectively, and eggs, with six votes, ranked second only to pie—I’m a big fan of eggs. But the fascinating part of my food web was in the middle range. Onions, chicken, and pot roast had four votes each. A dead tie.
How could this be? I had envisioned a clear, descending scale of taste preference: The favorite (pie) would get seven votes, the least favorite (potatoes) would get zero, and the others would sort themselves out in between. If I had simply ranked the eight foods, it would have been easy to score them from zero to seven with no ties. But a different pattern emerged from the round-robin-style “tournament.” I like pot roast better than onions, onions better than chicken, and chicken better than pot roast, but this leaves me with a triangle of onions, chicken, and pot roast. A > B and B > C, but, illogically, C > A.
This is exactly how mathematicians depict round-robin tournaments using graph theory, the study of relationships between collections of objects.
Triangles in these tournaments are quite common, despite our assumptions about rigid order. Winners aren’t always clear, as the tennis World Tour Finals demonstrated in 2006. Mathematicians even have a name for circular results, calling a round-robin tournament “paradoxical” when every player loses at least one head-to-head match. These are the same triangles noticed by Thorleif Schjelderup-Ebbe in the early 1900s within the pecking order in his chicken coop in Norway.
Where Thor left off, sociologist/statistician H. G. Landau picked up in the 1950s. Landau had studied ballistics during World War II, but after the war ended, he focused his attention on biological phenomena, eventually settling on chickens.
Like Thor, Landau observed that, in any given pair of hens, one would always dominate the other, even if the two birds were separated and reunited years later. Landau analyzed in precise detail the hierarchies of chicken coops. Unlike his Norwegian predecessor, though, he focused more on the circular rather than linear nature of these relationships. As in our favorite-foods exercise, Landau assigned each bird a dominance score; he called the top-scoring birds “king chickens” and tried to quantify their relationships to the other birds.
Not only were there frequent triangles, but some coops had multiple kings, at odds with our general perception of pecking orders. Landau showed that it was even possible for every single chicken in a coop to be a king while they all maintained stable and unequal dominance relationships with each other, in one perfectly circular hierarchy. If pecking orders were Thor’s legacy, then the idea that they could be circular became Landau’s claim to fame. Backed by the mathematician’s careful proofs, this concept has been handed down today in the form of Landau’s so-called king chicken theorems.
These theorems, which quantify the possible results of graphical tournaments, apply to many things besides chickens. They show why those round-robin events often don’t work in professional sports. The winner of a tennis match depends largely on how the two players’ styles complement each other as well as other factors beyond skill, such as the court surface, weather, and audience. The best players constantly beat each other in one event and take revenge at the next. That’s where great rivalries come from, and why we are enthralled by sports. Even the best players can lose to lesser opponents. And, as Landau showed, sometimes there is no “best” player at all, even if every individual matchup is perfectly predictable.
This is also why we have trouble ranking our favorite foods.
Theoretically, we should be able to arrange a strict, hierarchical list, but the differences between adjacent entries on that list are often small enough that other variables—presentation, mood, perception—have a greater impact when we are deciding what to have for dinner. Like a tennis match, favorite foods depend on immediate conditions as much as absolute flavor.
Pecking orders break down completely in chicken coops when the total number of birds exceeds about thirty, probably because chickens have trouble recognizing more than thirty familiar faces. At that point, the birds can’t keep track of one another closely enough to enforce dominance, and, instead of a transitive society, the group becomes egalitarian. All members are socially equal. (The numerical limit for social groups entails its own fascinating field of study; check out Dunbar’s number, which holds that typical humans are limited to about 150 friends in their social sphere, beyond which acquaintances are essentially strangers.)
Egalitarian societies sound great, but they have their own problems. In large chicken coops, such as industrial farms with tens of thousands of birds crammed together, aggression is still present—but, with no established order of dominance through which to channel those feelings, aggressive actions are dealt out randomly. Sometimes this even leads to bloodlust, an ugly manifestation of chicken personality that seems senseless in today’s high-productivity farm operations. If we could completely weed out aggression from chicken society, wouldn’t we all be better off?
One man thought so. In 1989, he set out to bring peace to the world, one chicken at a time.
—
EVEN WHILE RANDALL WISE
attended college and founded a successful software company in Boston, he couldn’t stop thinking about chickens.
Randall’s father, Irvin Wise, had managed a chicken farm in Northern California since the 1960s, and the old man always took an intense interest in chicken behavior, often involving his son in serious discussions about poultry. Mostly, why did those darned birds fight so much? If the hens could get along better, their farm would save money, because stressed-out chickens ate more feed, expended less energy on laying eggs, and nursed unnecessary pecking wounds. Randall listened carefully and, working with his father, hatched an idea.