The Sleepwalkers (152 page)

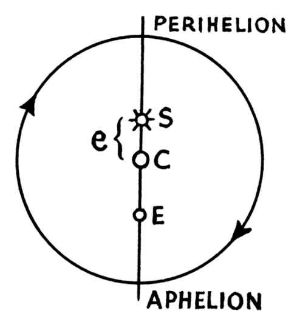
He
chose
out
of
Tycho's
treasure
four
observed
positions
of
Mars
at
the
convenient
dates
when
the
planet
was
in
opposition
to
the
sun.
⁸
The
geometrical
problem
which
he
had
to
solve
was,
as
we
saw,
to
determine,
out
of
these
four
positions,
the
radius
of
the
orbit,
the
direction
of
the
axis,
and
the
position
of
the
three
central
points
on
it.
It
was
a
problem
which
could
not
be
solved
by
rigorous
mathematics,
only
by
approximation,
that
is,
by
a
kind
of
trial-and-error
procedure
which
has
to
be
continued
until
all
the
pieces
in
the
jig-saw
puzzle
fit
together
tolerably
well.
The
incredible
labour
that
this
involved
may
be
gathered
from
the
fact
that
Kepler's
draft
calculations
(preserved
in
manuscript)
cover
nine
hundred
folio
pages
in
small
handwriting.

At
times
he
was
despairing;
he
felt,
like
Rheticus,
that
a
demon
was
knocking
his
head
against
the
ceiling,
with
the
shout:
"These
are
the
motions
of
Mars."
At
other
times,
he
appealed
for
help
to
Maestlin
(who
turned
a
deaf
ear),
to
the
Italian
astronomer,
Magini
(who
did
the
same),
and
thought
of
sending
an
S.O.S.
to
Francois
Vieta,
the
father
of
modem
algebra:
"Come,
oh
Gallic
Appollonius,
bring
your
cylinders
and
spheres
and
what
other
geometer's
houseware
you
have..."
^8a
But
in
the
end
he
had
to
slog
it
out
alone,
and
to
invent
his
mathematical
tools
as
he
went
along.

Half-way
through
that
dramatic
sixteenth
chapter,
he
bursts
out:

"If
thou
[dear
reader]
art
bored
with
this
wearisome
method
of
calculation,
take
pity
on
me
who
had
to
go
through
with
at
least
seventy
repetitions
of
it,
at
a
very
great
loss
of
time;
nor
wilst
thou
be
surprised
that
by
now
the
fifth
year
is
nearly
past
since
I
took
on
Mars..."

Now,
at
the
very
beginning
of
the
hair-raising
computations
in
chapter
sixteen,
Kepler
absentmindedly
put
three
erroneous
figures
for
three
vital
longitudes
of
Mars,
and
happily
went
on
from
there,
never
noticing
his
error.
The
French
historian
of
astronomy,
Delambre,
later
repeated
the
whole
computation,
but,
surprisingly,
his
correct
results
differ
very
little
from
Kepler's
faulty
ones.
The
reason
is,
that
toward
the
end
of
the
chapter
Kepler
committed
several
mistakes
in
simple
arithmetic
–
errors
in
division
which
would
bring
bad
marks
to
any
schoolboy
–
and
these
errors
happen
very
nearly
to
cancel
out
his
earlier
mistakes.
We
shall
see,
in
a
moment,
that,
at
the
most
crucial
point
of
the
process
of
discovering
his
Second
Law,
Kepler
again
committed
mathematical
sins
which
mutually
cancelled
out,
and
"as
if
by
miracle"
(in
his
own
words),
led
to
the
correct
result.

At
the
end
of
that
breathtaking
chapter,
Kepler
seems
to
have
triumphantly
achieved
his
aim.
As
a
result
of
his
seventy-odd
trials,
he
arrived
at
values
for
the
radius
of
the
orbit
and
for
the
three
central
points
which
gave,
with
a
permissible
error
of
less
than
2
′
,
the
correct
positions
of
Mars
for
all
the
ten
oppositions
recorded
by
Tycho.
The
unconquerable
Mars
seemed
at
last
to
have
been
conquered.
He
proclaimed
his
victory
with
the
sober
words:

"Thou
seest
now,
diligent
reader,
that
the
hypothesis
based
on
this
method
not
only
satisfies
the
four
positions
on
which
it
was
based,
but
also
correctly
represents,
within
two
minutes,
all
the
other
observations..."
⁹

There
follow three pages of tables to prove the correctness of his claim;
and then, without further transition, the next chapter starts with
the following words:

"Who
would
have
thought
it
possible?
This
hypothesis,
which
so
closely
agrees
with
the
observed
oppositions,
is
nevertheless
false..."

4.
The Eight Minutes Arc

In
the
two
following
chapters
Kepler
explains,
with
great
thoroughness
and
an
almost
masochistic
delight,
how
he
discovered
that
the
hypothesis
is
false,
and
why
it
must
be
rejected.
In
order
to
prove
it
by
a
further
test,
he
had
selected
two
specially
rare
pieces
from
Tycho's
treasury
of
observations,
and
lo!
they
did
not
fit;
and
when
he
tried
to
adjust
his
model
to
them,
this
made
things
even
worse,
for
now
the
observed
positions
of
Mars
differed
from
those
which
his
theory
demanded
by
magnitudes
up
to
eight
minutes
arc.