The Sleepwalkers (115 page)

____________________

In
the
Preface
to
the
work,
Kepler
explained
how
he
came
to
make
his
"discovery".
While
still
a
student
in
Tuebingen,
he
had
heard
from
his
teacher
in
astronomy,
Maestlin,
about
Copernicus,
and
agreed
that
the
sun
must
be
in
the
centre
of
the
universe
"for
physical,
or
if
you
prefer,
for
metaphysical
reasons".
He
then
began
to
wonder
why
there
existed
just
six
planets
"instead
of
twenty
or
a
hundred",
and
why
the
distances
and
velocities
of
the
planets
were
what
they
were.
Thus
started
his
quest
for
the
laws
of
planetary
motion.

At
first
he
tried
whether
one
orbit
might
perchance
be
twice,
three
of
four
times
as
large
as
another.
"I
lost
much
time
on
this
task,
on
this
play
with
numbers;
but
I
could
find
no
order
either
in
the
numerical
proportions
or
in
the
deviations
from
such
proportions."
He
warns
the
reader
that
the
tale
of
his
various
futile
efforts
"will
anxiously
rock
thee
hither
and
thither
like
the
waves
of
the
sea".
Since
he
got
nowhere,
he
tried
"a
startlingly
bold
solution":
he
inserted
an
auxiliary
planet
between
Mercury
and
Venus,
and
another
between
Jupiter
and
Mars,
both
supposedly
too
small
to
be
seen,
hoping
that
now
he
would
get
some
sensible
sequence
of
ratios.
But
this
did
not
work
either;
nor
did
various
other
devices
which
he
tried.

"I
lost
almost
the
whole
of
the
summer
with
this
heavy
work.
Finally
I
came
close
to
the
true
facts
on
a
quite
unimportant
occasion.
I
believe
Divine
Providence
arranged
matters
in
such
a
way
that
what
I
could
not
obtain
with
all
my
efforts
was
given
to
me
through
chance;
I
believe
all
the
more
that
this
is
so
as
I
have
always
prayed
to
God
that
he
should
make
my
plan
succeed,
if
what
Copernicus
had
said
was
the
truth."
²

The
occasion
of
this
decisive
event
was
the
aforementioned
lecture
to
his
class,
in
which
he
had
drawn,
for
quite
different
purposes,
a
geometrical
figure
on
the
blackboard.
The
figure
showed
(I
must
describe
it
in
a
simplified
manner)
a
triangle
fitted
between
two
circles;
in
other
words,
the
outer
circle
was
circumscribed
around
the
triangle,
the
inner
circle
inscribed
into
it.

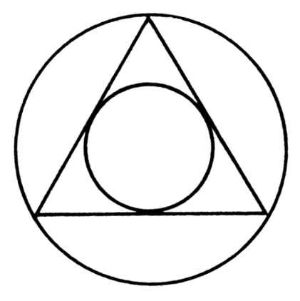
As
he
looked
at
the
two
circles,
it
suddenly
struck
him
that
their
ratios
were
the
same
as
those
of
the
orbits
of
Saturn
and
Jupiter.
The
rest
of
the
inspiration
came
in
a
flash.
Saturn
and
Jupiter
are
the
"first"
(i.e.
the
two
outermost)
planets,
and
"the
triangle
is
the
first
figure
in
geometry.
Immediately
I
tried
to
inscribe
into
the
next
interval
between
Jupiter
and
Mars
a
square,
between
Mars
and
Earth
a
pentagon,
between
Earth
and
Venus
a
hexagon..."

It
did
not
work
–
not
yet,
but
he
felt
that
he
was
quite
close
to
the
secret.
"And
now
I
pressed
forward
again.
Why
look
for
two-dimensional
forms
to
fit
orbits
in
space?
One
has
to
look
for
three-dimensional
forms
–
and,
behold
dear
reader,
now
you
have
my
discovery
in
your
hands!
..."

The
point
is
this.
One
can
construct
any
number
of
regular
polygons
in
a
two-dimensional
plane;
but
one
can
only
construct
a
limited
number
of
regular
solids
in
three-dimensional
space.
These
"perfect
solids",
of
which
all
faces
are
identical,
are:
(1)
the
tetrahedron
(pyramid)
bounded
by
four
equilateral
triangles;
(2)
the
cube;
(3)
the
octahedron
(eight
equilateral
triangles);
(4)
the
dodecahedron
(twelve
pentagons)
and
(5)
the
icosahedron
(twenty
equilateral
triangles).