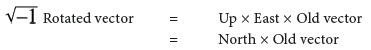The Eternal Flame (34 page)
Authors: Greg Egan
Tags: #Science Fiction, #General, #Space Opera, #Fiction

Patrizia warmed to the idea. “Luxagens have no polarization—wrong! Polarizations only come in threes—wrong! Any number of luxagens can share the same state—wrong again! I think that would cover it.”
Carla said, “The first one’s just an empirical question, but the second one’s going to take some thought.” She glanced at the clock on the wall; she’d told Carlo she’d meet him in his apartment by the sixth bell, but he knew better than to expect her to be on time. “Why do we assume that polarizations come in threes? For light, you have two vectors in four-space: the direction of the light field itself, and the direction of the light’s future. If I see a bit of light over here, and you see a bit of light over there, then I ought to be able to grab the two vectors that describe my light and rotate them together in four-space so they agree with those describing your light. That’s the absolute core of rotational physics: if we couldn’t do that, your light and my light wouldn’t deserve to be called by the same name.”
Patrizia said, “If the vectors are constrained to be perpendicular, they’ll look perpendicular to everyone. Fix the direction of the light’s history through four-space, and that leaves you with three perpendicular choices for the field—three polarizations.”
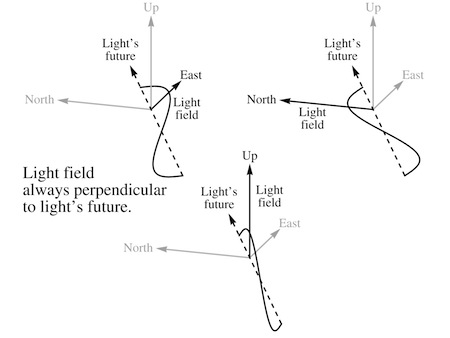
“You can imagine a case where they’re parallel instead,” she added. “Everyone would agree on that too. But you could never rotate one kind of light into the other, so there’d be no reason to classify them as the same thing at all.”
“So what are the choices?” Romolo said. “Light has three polarizations, but the alternative where the vectors are parallel only has one.”
“A luxagen wave takes complex values,” Carla reminded him. “So it has a kind of two-dimensional character to it already, if you think of real and imaginary numbers as pointing in perpendicular directions. But that doesn’t double the possibilities for polarization. You can rotate a luxagen wave by any angle at all in the complex plane without changing the physical state it describes.”
“So it
halves
the possibilities,” Patrizia said. “A complex wave looks two dimensional, but it really only has one dimension.”
“Half four is two,” Romolo noted. “Half the size of an ordinary four-vector gives us the number of polarizations we’re seeing. Does that help?”
Carla wasn’t sure, but it was worth checking. “Suppose a luxagen wave consists of
two
complex numbers, for the two polarizations,” she said. “Each one has a real part and an imaginary part, so all in all that’s four dimensions.”
“So you just think of the usual four dimensions as two complex planes?” Romolo suggested.
“Maybe,” Carla replied. “But what happens when you rotate something? If you’ve got two complex numbers that describe a luxagen’s polarization, and I come along and physically turn that luxagen upside-down… what happens to the complex numbers?”
Romolo said, “Wouldn’t you just take their real and imaginary parts, and apply the usual rules for rotating a vector?”
“That’s the logical thing to try,” Carla agreed. “So let’s see if we can make it work.”
The simplest way to describe rotations in four-space was with vector multiplication and division, so Carla brought the tables onto her chest as a reminder.
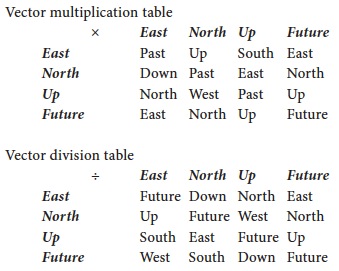
Any rotation could be achieved by multiplying on the left with one vector and dividing on the right by another; the choice of those two vectors determined the overall rotation. Romolo worked through an example, choosing Up for both operations.
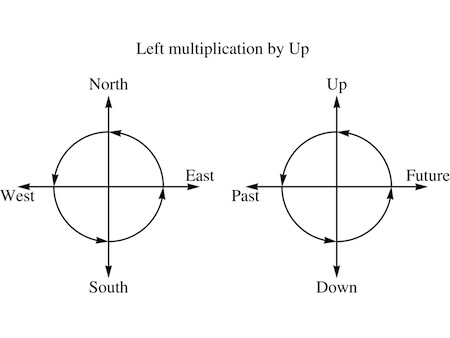
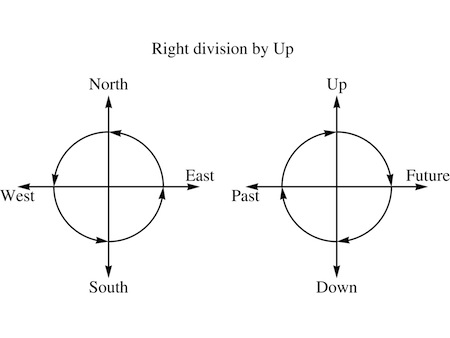
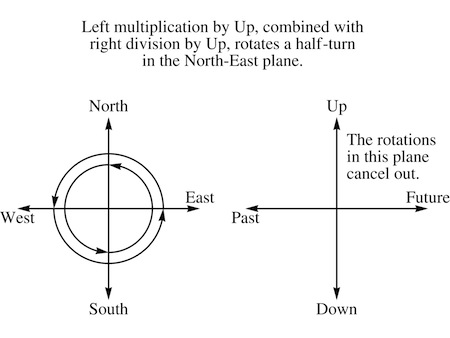
“There’s one thing we’ll need to get right if we’re going to make this work,” Carla realized. “Given a pair of complex numbers, if you multiply them both by the square root of minus one that will affect each number separately. It doesn’t mix them up in any way—it just rotates each complex plane by a quarter-turn, making real numbers imaginary and imaginary numbers real. So if we’re going to treat two planes in four-space as complex number planes, we’ll need some equivalent operation.”
“But I just drew that!” Romolo replied. “Multiplication on the left by Up rotates everything in the Future-Up plane by a quarter turn, and everything in the North-East plane by a quarter turn. Vectors in one plane aren’t moved to the other. Do it twice—square it—and you get a half turn in both planes, which multiplies everything by minus one. So we could treat those two planes as the two complex numbers, and use left-multiplication by Up as the square root of minus one!”
Carla wasn’t satisfied yet. “All right, that works perfectly on its own. But what happens when you physically rotate the luxagen as well? If I rotate an ordinary vector and then double it, or double it first and then rotate it, the end result has to be the same, right?”
“Of course.” Romolo was puzzled, but then he saw what she was getting at. “So whatever we use to multiply by the square root of minus one has to give the same result whether we rotate first and then multiply, or vice versa.”
“Exactly.”
Patrizia looked dubious. “I don’t think that’s going to be possible,” she said. “What about the rotation you get by multiplying on the left with East and dividing on the right by Future? Future acts like one, it has no effect, so you get:”

“Romolo’s definition of multiplying by the square root of minus one is:”
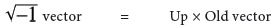
“Follow that with the rotation:”
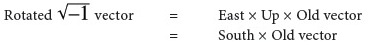
“But now do the rotation first, and then multiply by the square root of minus one:”