The Dancing Wu Li Masters (10 page)
Read The Dancing Wu Li Masters Online
Authors: Gary Zukav

When we put wave mechanics and Planck’s discovery together we get this: High-frequency light, such as violet light, has a short wavelength and high energy; low-frequency light, such as red light, has a long wavelength and low energy.
This explains the photoelectric effect. Photons of violet light knock electrons loose from the atoms of a metal and send them flying away at a higher velocity than photons of red light because the photons of violet light, which is a high-frequency light, have more energy than the photons of red light, which is a low-frequency light.
This all makes sense if you overlook the fact that we are talking about particles (photons) in terms of waves (frequencies) and waves in terms of particles, which, of course, makes no sense at all.
If you feel that you understand the last few pages, congratulations! You have mastered the most difficult mathematics in the book. If not, go back and reread these pages. It is easy to dance with wavelengths and frequencies if you know how they are connected.
Waves are playful creatures that like to do dances of their own. For example, under certain conditions they bend around corners. When this happens it is called diffraction.
Imagine that we are in a helicopter hovering over the mouth of an artificial harbor. The mouth of the harbor is wide enough for two aircraft carriers to pass each other going through it. The sea is rough and the wind and waves are blowing straight into the mouth of the
harbor. When we look down, this is the pattern that we see the waves making in the harbor:
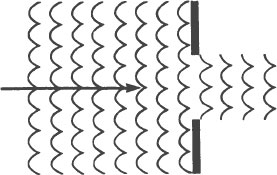
The waves are stopped cleanly by the walls of the harbor except at the harbor entrance, where they continue straight forward into the harbor until they are dissipated.
Now imagine that the mouth of the harbor is so small that a rowboat scarcely can pass through it. As we look down from the helicopter, the pattern we see is quite different.
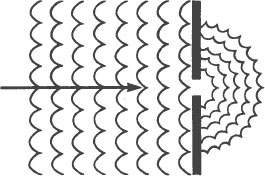
Instead of moving directly ahead into the harbor, the waves inside the harbor are spreading out from the mouth of the harbor almost as if it
were a pond and we had dropped a rock into it at that point. This is diffraction.
Why does it happen? Why does reducing the size of the harbor mouth cause the wave pattern inside the harbor to spread out in semi-circles?
The answer lies in comparing the size of the harbor mouth to the size of the wavelength of the incoming waves. In the first case, the size of the harbor mouth is considerably larger than the distance between the crests of the waves going through it, and the waves proceed directly through it into the harbor following a straight line (rectilinear propagation) as waves usually do.
In the second case, the size of the harbor mouth is about the same size, or smaller, than the wavelength of the incoming waves, and when this happens, it causes the characteristic pattern (diffraction) that we see in the drawing.
Whenever waves pass through an opening that is so small that the wavelength of the waves passing through it seems large in comparison, the waves passing through it diffract.
Since light is a wave phenomenon (according to the wave theory of light), it should behave in the same way, and it does. If we place a light source behind a cut-out like the one below, it casts a projection on the wall like this one:
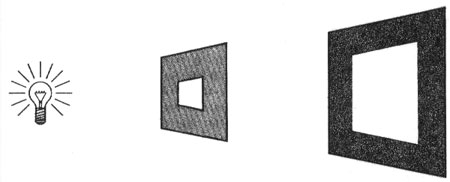
This is analogous to sea waves entering the large harbor mouth. The width of the cut-out is millions of times larger than the wavelength of the light. As a result, the light waves go straight through it,
following straight lines and projecting onto the wall a figure with the same shape as the cut-out. Notice especially that this projection has distinct borders between the bright area and the dark area.
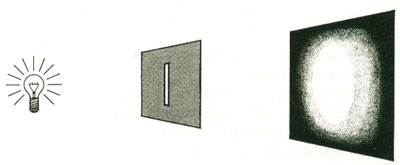
If we make the cut-out no larger than a razor slit so that its width is roughly as small as the wavelength of the incoming light, the light diffracts. Now the sharp boundary between the light area and the dark area disappears and we see a bright area that fades into darkness at the edges. Instead of proceeding in a straight line to the wall, the light beam has spread out like a fan. This is diffracted light.
Now that you know the punch line, here comes the story.
In 1803, Thomas Young settled once and for all (he thought) the question of the nature of light. He used an experiment that was both simple and dramatic. In front of a light source (Young used sunlight coming through a hole in a screen) he placed a screen with two vertical slits in it. Each slit could be covered over with a piece of material.

On the other side of the double-slit screen was a wall against which the light coming through the double slits could shine. When the light source was turned on and one of the slits was covered up, the wall was illuminated like the drawing below.
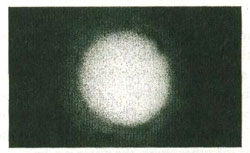
When both slits were uncovered, however, Young made history. The projection on the wall should have been the sum of the light from the two slits, but it wasn’t. Instead, the wall was illuminated with alternating bands of light and darkness! The center band was the brightest. On both sides of the center band of light were bands of darkness; then bands of light, but less intense than the center band; then bands of darkness, etc., as below.

How could this happen?
The simplicity of the answer is what makes this experiment a great one. The alternating light and dark bands are a well-known phenomenon of wave mechanics called interference. Interference results when the waves of light diffracting from the two slits interfere with
each other. In some places these waves overlap and reinforce one another. In other places they cancel each other.
In areas where one wave crest overlaps another wave crest, the result is an intensification of light (the light bands). In areas where a crest meets a trough, they cancel each other and no light reaches the wall (the dark bands).
It is just as if we dropped two stones into a pond simultaneously and watched the waves spreading from their points of entry. The waves that the stones make interfere with each other. In places where the crests of the waves caused by one stone meet the crests of the waves caused by the other stone, large waves result. In places where the troughs of the waves caused by one stone meet the crests of the waves caused by the other stone, the water is calm.
In short, Young’s double-slit experiment showed that light must be wave-like because only waves can create interference patterns. The situation, then, was as follows: Einstein, using the photoelectric effect, “proved” that light is particle-like and Young, using the phenomenon of interference, “proved” that light is wave-like. But a wave cannot be a particle and a particle cannot be a wave.
That is just the beginning! Since Einstein “proved” that light is composed of photons, let us go back to Young’s double-slit experiment and run it with photons.
*
(This has been done.) Suppose that we have a light gun which can fire, in effect, one photon at a time. The experiment is set up as before, except that only one slit is open. Now we fire the photon, it goes through the open slit, and we mark where it hits the wall (using a photographic plate). Because we have done this experiment before, we notice that the photon has landed in an area that would be dark if the second slit were open. That is, if the second slit were open, no photons would be recorded in this area.
To make sure, we do the experiment again, but this time we leave both of the slits open. Just as we thought, there are no photons recorded now in the area where the photon hit in our first experiment.
When both slits are open and interference is present, this area is in the middle of a dark band.