The Cosmic Landscape (38 page)

Let’s begin with a snowflake. Every child knows that no two snowflakes are exactly alike, but they nevertheless all share a certain feature: a symmetry. Just looking at a snowflake, you can easily see its symmetry. Take the snowflake and rotate it by an angle. It will look different, tilted. But if you rotate it by exactly 60 degrees, it will look unchanged. A physicist would say that rotating a snowflake through 60 degrees is a symmetry.

Symmetries are concerned with the operations you can do to a system that don’t change the results of experiments. In the case of the snowflake, the operation is to rotate it by 60 degrees. Here is another example: suppose we build an experiment to determine the acceleration due to gravity at the earth’s surface. The simplest version would be to drop a rock from a known height and time its fall. The answer is approximately ten meters per second per second. Notice that I didn’t bother to tell you where I dropped the rock, whether it was in California or Calcutta. To a pretty good approximation, the answer is the same everywhere on the earth’s surface: the result of the experiment would not change if you moved the entire experiment from one point of the earth’s surface to another. In physics jargon moving or displacing something from one point to another is called a translation. So we speak about the symmetry of the earth’s gravitational field “under translation.” Of course some annoying irrelevant effect might contaminate the symmetry. For example, if we did the experiment just above a very large and heavy mineral deposit, we would get a slightly bigger result. In that case we would say that the symmetry is only approximate. Approximate symmetries are also called
broken symmetries.
The presence of the localized mineral deposit “broke the translation symmetry.”

Can the symmetry of the snowflake be broken? No doubt some snowflakes are not perfect. If the flake formed in less than ideal conditions, one side might be a little different from the others. You might still be able to detect the overall hexagon shape of the crystal, but it would have an imperfect, or broken, symmetry.

In outer space, far from any contaminating influences, we might measure the gravitational force between two masses and deduce Newton’s law of gravity. No matter where we did the experiment, we would get the same answer. So Newton’s law of gravity has translation invariance.

To measure the force law between two objects, you have to separate them along some direction in space. For example, you might measure the force by separating the masses along the x-axis or along the y-axis or any other direction for that matter. Could the force between two objects depend on the direction along which they are separated? In principle, yes, but only if the laws of nature were different from what they are. It’s a fact of nature that Newton’s law of gravity—force proportional to the product of masses and inversely proportional to the square of the distance—is the same in every direction. If the whole experiment were rotated in space to realign the separation, the results would be unchanged. This insensitivity to direction is called
rotation symmetry.
Translation and rotation symmetries are two of the most basic properties of the world we live in.

Look at yourself in the mirror as you get dressed in the morning. Your mirror image looks exactly the same as you do. The mirror image of your pants is exactly the same as your real pants. The mirror image of your left glove is the same as your left glove.

Wait—that’s wrong. Look again. The mirror image of your left glove is not at all like the real left glove. It’s identical to the real right glove! And the image of the right glove is actually a left glove.

Look a little more closely at your own mirror image. It’s not you. The freckle on your left cheek is on the right cheek of the mirror image. If you could open up your chest cavity, you would find something really strange about the image. Its heart would be on the right side. It’s like no real human being. Let’s call it a .

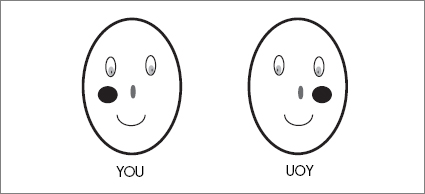
Let’s imagine that we had a futuristic technology that allowed us to build up any object we pleased by assembling atoms, one by one. Here is an interesting project. Let’s build a human whose mirror image is exactly like you—heart on the left, freckle on the left, and so on. Now the original would be a .

Does the work? Will it breathe? Will its heart work? If we feed it will it metabolize the sugar that we give it? Mostly the answers are yes. It will work as well as you do. But we will find a problem with its metabolism. It just won’t process ordinary sugar.

The reason is that sugar comes in two types just like gloves—left-handed and right-handed. Humans can metabolize only sugar. A can metabolize only . The ordinary sugar molecule comes in two varieties—the kind you eat and its mirror image, which you can’t. The technical names for sugar and are of course levulose (left-handed sugar molecules that we eat) and dextrose (right-handed sugar that we don’t metabolize).
will work just as well as humans but only if you also replace everything in their environment, including their food, by reflected counterparts.

Replacing everything by its mirror image is called
reflection symmetry
or sometimes
parity symmetry.
The implication of this symmetry is probably clear, but let’s spell it out. If everything in the world is replaced by its mirror image, the world will behave in a completely unchanged way.

In actual fact reflection symmetry is not exact. It is an example of a broken symmetry. Something causes the mirror image of a neutrino to be many times heavier than the original. This infects other particles but only in the minutest way. It is as if nature’s mirror were a slightly distorted mirror—a funhouse mirror that gives a distorted image, but only very slightly. The distortion is so insignificant for ordinary matter that s would not notice at all. But high-energy elementary particles do notice the distortion and behave in ways that their mirror images don’t. However, let’s ignore the distortion for the time being and pretend that reflection symmetry is an exact symmetry of nature.

What do we mean when we say that “a symmetry relates particles”? Simply stated, it means that for each type of particle there is a partner or a twin with closely related properties. For reflection symmetry it means that if a left glove is possible, so is a right glove—if levulose can exist, so can dextrose. And if reflection symmetry were not broken, this would apply to every elementary particle. Every particle would have an identical but reflected twin. When reflecting humans to make
, every elementary particle must be replaced by its twin.

Antimatter is another manifestation of symmetry called charge
conjugation symmetry
. Once again, the symmetry involves replacing everything by something else: in this case every particle is replaced by its antiparticle. That replaces a positive electric charge, such as the proton, by a negative charge—the antiproton. Likewise, a positron replaces every ordinary negative electron. Hydrogen atoms become antihydrogen atoms consisting of a positron and an antiproton. Such antiatoms have actually been made in the laboratory—just a handful, not enough to make even an antimolecule. But no one doubts that antimolecules are possible. Antihumans are possible but don’t forget to feed them antifood. In fact you’d best keep away from antipeople. When matter meets antimatter it explosively annihilates into a burst of photons. The explosion that would occur if you inadvertently shook hands with an antihuman would be similar to a nuclear bomb explosion.

As it turns out charge conjugation symmetry is also a slightly broken symmetry. But as with reflections the effect would be completely insignificant except for very high-energy particles.

Now back to fermions and bosons. The original String Theory, the one that Nambu and I discovered, is called
bosonic String Theory
because all the particles that it describes are bosons. This was not a good thing for describing hadrons: after all, the proton is a fermion. Neither would it be good if the goal of String Theory were a theory of everything. Electrons, neutrinos, quarks—they are all fermions. But it didn’t take long before new versions of String Theory were discovered that contained fermions as well as bosons. And one of the remarkable mathematical properties of these so-called superString Theories is supersymmetry—the symmetry between bosons and fermions that requires particles to come in exactly matched pairs, a boson for every fermion and vice versa.

Supersymmetry is, again, an indispensable and very powerful mathematical tool for string theorists. Without it the mathematics is so hard that it is very difficult to be certain of the consistency of the theory. Almost all of the reliable work on the subject assumed the world was supersymmetric. But as I emphasized, supersymmetry is most definitely not an exact symmetry of nature. At best it is a fairly badly broken symmetry—the kind of distorted symmetry that a badly warped funhouse mirror would imply. In fact no superpartner has ever been discovered for any of the known elementary particles. If a boson existed with the same mass and charge as the electron, it would have been discovered long ago. Nevertheless, if you go to your Web browser and look up research papers in elementary-particle physics, you will find that since the mid-1970s the overwhelming majority have something to do with supersymmetry. Why is this? Why didn’t theoretical physicists toss out supersymmetry in disgust and, with it, superString Theory? The reasons vary.

The subject that was once called theoretical high-energy physics, or theoretical elementary-particle physics, long ago split into two separate disciplines called
phenomenology
and
theory.
If you type in the URL
http://arXiv.org
on your Web browser, you’ll find the site where physicists post their research papers. Separate subdisciplines are listed by subject: nuclear theory, condensed-matter physics, and so on. If you look for high-energy physics (hep), you will find four separate archives, only two of which are devoted to the theoretical aspects of the subject that concern us (the other two are for experimental physics and computer simulations). One archive (hep-ph) is for phenomenology (the meaning of which will become clear shortly). The other (hep-th) is for the more theoretical and mathematical papers. Open them both. You’ll find that the hep-ph papers are all about the problems of conventional-particle physics. They sometimes refer to experiments, either past or future, and the results of the papers are often numbers and graphs. By contrast, the hep-th papers are largely about String Theory and gravity. They are more mathematical, and for the most part, they have little to do with experiments. However, in the last few years, the lines between these sub-subdisciplines have been blurred a good deal, which I think is a good sign.