The Code Book (63 page)

The recipient, who also knows the keyword, can easily decipher the ciphertext by simply reversing the process: for example, enciphered letters in the same row are deciphered by replacing them by the letters to their left.
As well as being a scientist, Playfair was also a notable public figure (Deputy Speaker of the House of Commons, postmaster general, and a commissioner on public health who helped to develop the modern basis of sanitation) and he was determined to promote Wheatstone’s idea among the most senior politicians. He first mentioned it at a dinner in 1854 in front of Prince Albert and the future Prime Minister, Lord Palmerston, and later he introduced Wheatstone to the Under Secretary of the Foreign Office. Unfortunately, the Under Secretary complained that the system was too complicated for use in battle conditions, whereupon Wheatstone stated that he could teach the method to boys from the nearest elementary school in 15 minutes. “That is very possible,” replied the Under Secretary, “but you could never teach it to attachés.”
Playfair persisted, and eventually the British War Office secretly adopted the technique, probably using it first in the Boer War. Although it proved effective for a while, the Playfair cipher was far from impregnable. It can be attacked by looking for the most frequently occurring digraphs in the ciphertext, and assuming that they represent the commonest digraphs in English: th, he, an, in, er, re, es.
Appendix F
The ADFGVX Cipher
The ADFGVX cipher features both substitution and transposition. Encryption begins by drawing up a 6 × 6 grid, and filling the 36 squares with a random arrangement of the 26 letters and the 10 digits. Each row and column of the grid is identified by one of the six letters A, D, F, G, V or X. The arrangement of the elements in the grid acts as part of the key, so the receiver needs to know the details of the grid in order to decipher messages.

The first stage of encryption is to take each letter of the message, locate its position in the grid and substitute it with the letters that label its row and column. For example, 8 would be substituted by AA, and
p
would be replaced by AD. Here is a short message encrypted according to this system:

So far this is a simple monoalphabetic substitution cipher, and frequency analysis would be enough to crack it. However, the second stage of the ADFGVX is a transposition, which makes cryptanalysis much harder. The transposition depends on a keyword, which in this case happens to be the word MARK, and which must be shared with the receiver. Transposition is carried out according to the following recipe. First, the letters of the keyword are written in the top row of a fresh grid. Next, the stage 1 ciphertext is written underneath it in a series of rows, as shown below. The columns of the grid are then rearranged so that the letters of the keyword are in alphabetical order. The final ciphertext is achieved by going down each column and then writing out the letters in this new order.
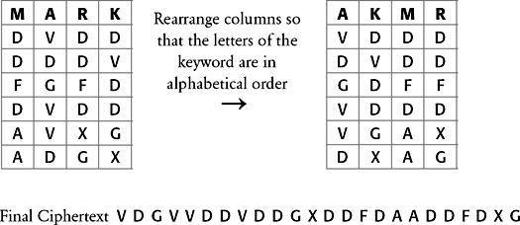
The final ciphertext would then be transmitted in Morse code, and the receiver would reverse the encryption process in order to retrieve the original text. The entire ciphertext is made up of just six letters (i.e. A, D, F, G, V, X), because these are the labels of the rows and columns of the initial 6 × 6 grid. People often wonder why these letters were chosen as labels, as opposed to, say, A, B, C, D, E and F. The answer is that A, D, F, G, V and X are highly dissimilar from one another when translated into Morse dots and dashes, so this choice of letters minimizes the risk of errors during transmission.
Appendix G
The Weaknesses of Recycling a Onetime Pad
For the reasons explained in
Chapter 3
, ciphertexts encrypted according to a onetime pad cipher are unbreakable. However, this relies on each onetime pad being used once and only once. If we were to intercept two distinct ciphertexts which have been encrypted with the same onetime pad, we could decipher them in the following way.
We would probably be correct in assuming that the first ciphertext contains the word the somewhere, and so cryptanalysis begins by assuming that the entire message consists of a series of the’s. Next, we work out the onetime pad that would be required to turn a whole series of the’s into the first ciphertext. This becomes our first guess at the onetime pad. How do we know which parts of this onetime pad are correct?
We can apply our first guess at the onetime pad to the second ciphertext, and see if the resulting plaintext makes any sense. If we are lucky, we will be able to discern a few fragments of words in the second plaintext, indicating that the corresponding parts of the onetime pad are correct. This in turn shows us which parts of the first message should be the.
By expanding the fragments we have found in the second plaintext, we can work out more of the onetime pad, and then deduce new fragments in the first plaintext. By expanding these fragments in the first plaintext, we can work out more about the onetime pad, and then deduce new fragments in the second plaintext. We can continue this process until we have deciphered both plaintexts.
This process is very similar to the decipherment of a message enciphered with a Vigenère cipher using a key that consists of a series of words, such as the example in
Chapter 3
, in which the key was CANADABRAZILEGYPTCUBA.
Appendix H
The
Daily Telegraph
Crossword Solution
| ACROSS | DOWN |
| 1. Troupe | 1. Tipstaff |
| 4. Short Cut | 2. Olive oil |
| 9. Privet | 3. Pseudonym |
| 10. Aromatic | 5. Horde |
| 12. Trend | 6. Remit |
| 13. Great deal | 7. Cutter |
| 15. Owe | 8. Tackle |
| 16. Feign | 11. Agenda |
| 17. Newark | 14. Ada |
| 22. Impale | 18. Wreath |
| 24. Guise | 19. Right nail |
| 27. Ash | 20. Tinkling |
| 28. Centre bit | 21. Sennight |
| 31. Token | 23. Pie |
| 32. Lame dogs | 25. Scales |
| 33. Racing | 26. Enamel |
| 34. Silencer | 29. Rodin |
| 35. Alight | 30. Bogie |
Appendix I
Exercises for the Interested Reader
Some of the greatest decipherments in history have been achieved by amateurs. For example, Georg Grotefend, who made the first breakthrough in interpreting cuneiform, was a schoolteacher. For those readers who feel the urge to follow in his footsteps, there are several scripts that remain a mystery. Linear A, a Minoan script, has defied all attempts at decipherment, partly due to a paucity of material. Etruscan does not suffer from this problem, with over 10,000 inscriptions available for study, but it has also baffled the world’s greatest scholars. Iberian, another pre-Roman script, is equally unfathomable.
The most intriguing ancient European script appears on the unique Phaistos Disk, discovered in southern Crete in 1908. It is a circular tablet dating from around 1700
B.C
. bearing writing in the form of two spirals, one on each side. The signs are not handmade impressions, but were made using a variety of stamps, making this the world’s oldest example of typewriting. Remarkably, no other similar document has ever been found, so decipherment relies on very limited information-there are 242 characters divided into 61 groups. However, a typewritten document implies mass production, so the hope is that archaeologists will eventually discover a hoard of similar disks, and shed light on this intractable script.
One of the great challenges outside Europe is the decipherment of the Bronze Age script of the Indus civilization, which can be found on thousands of seals dating from the third millennium
B.C
. Each seal depicts an animal accompanied by a short inscription, but the meaning of these inscriptions has so far evaded all the experts. In one exceptional example the script has been found on a large wooden board with giant letters 37 cm in height. This could be the world’s oldest billboard. It implies that literacy was not restricted to the elite, and raises the question as to what was being advertised. The most likely answer is that it was part of a promotional campaign for the king, and if the identity of the king can be established, then the billboard could provide a way into the rest of the script.
Appendix J
The Mathematics of RSA
What follows is a straightforward mathematical description of the mechanics of RSA encryption and decryption.
(1) Alice picks two giant prime numbers,
p
and
q
. The primes should be enormous, but for simplicity we assume that Alice chooses
p
= 17,
q
= 11. She must keep these numbers secret.
(2) Alice multiplies them together to get another number,
N
. In this case
N
= 187. She now picks another number e, and in this case she chooses
e
= 7.
(e and (p − 1) × (q − 1) should be relatively prime, but this is a technicality.)
(3) Alice can now publish
e
and
N
in something akin to a telephone directory. Since these two numbers are necessary for encryption, they must be available to anybody who might want to encrypt a message to Alice. Together these numbers are called the public key. (As well as being part of Alice’s public key,
e
could also be part of everybody else’s public key. However, everybody must have a different value of N, which depends on their choice of
p
and q.)
(4) To encrypt a message, the message must first be converted into a number,
M
. For example, a word is changed into ASCII binary digits, and the binary digits can be considered as a decimal number.
M
is then encrypted to give the ciphertext,
C
, according to the formula
C = M
e
(mod
N
)
(5) Imagine that Bob wants to send Alice a simple kiss: just the letter
X
. In ASCII this is represented by 1011000, which is equivalent to 88 in decimal. So,
M
= 88.
(6) To encrypt this message, Bob begins by looking up Alice’s public key, and discovers that
N
= 187 and
e
= 7. This provides him with the encryption formula required to encrypt messages to Alice. With
M
= 88, the formula gives