The Case for Mars (15 page)

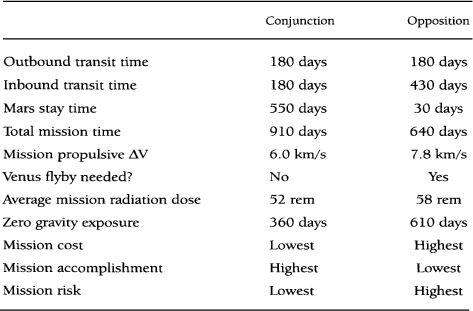
One example of a conjunction mission would be a “minimum energy” mission performed with two hmann transfers between Earth and Mars. Such a mission would be the cheapest way to travel, but would require 258-day transits each way. This is fine for cargo, but if you are flying crew it is desirable to speed things up a bit. It turns out that it doesn’t take too much extra propellant to cut the conjunction
transfer time to about 180 days, so that’s what we propose to do in the Mars Direct mission. However, if you adopt such a flight plan, you’ll need to stay 550 days on the Martian surface before your return launch window opens up, and thus your total round-trip mission time will be about 910 days.

The opposition mission has one of its legs, for example the outbound trip, accomplished in the same manner as the conjunction. The return leg, however, is then radically different. On the way home, a great deal of extra propellant is used to send the spacecraft from Mars, not back to Earth, but all the way to the inner solar system. There it swings by Venus, getting a gravity assist that slingshots it toward Earth. This procedure opens up a departure window soon after arrival at Mars. Even though the return trajectory takes considerably longer than a Hohmann transfer, an opposition mission cuts total mission time away from Earth by nearly ten months, from about 900 days down to 600 days or so.

Because it minimizes the total mission duration, NASA’s 90-Day Report designers favored the opposition mission. Others have followed suit, and assumed that opposition is the only way to go to Mars. But does such a preference make sense? The opposition mission has significantly larger propulsion requirements, needing 7.8 km/s of “delta-V” or ΔV, of total velocity change to speed up or slow down the spacecraft, compared to 6.0 km/s for the conjunction mission. (ΔV is the velocity change required to move a spacecraft from one orbit to another.) In fact, if space-storable propellants are used for the rocket burn that drives the spacecraft from its Mars parking orbit onto its trans-Earth trajectory, the opposition mission shown will have a launch mass about double that of the conjunction mission. It gets worse, however. The ΔV requirements given in
Table 4.1
are only for the mission’s acceleration maneuvers departing LEO and a highly elliptical Mars’ parking orbit; it is assumed that the spacecraft can aerobrake into Earth or Mars orbit. But the opposition mission spacecraft may be so massive that aerobraking proves impractical if not impossible. If that’s the case, rocket propulsion would also have to be used for deceleration, adding more ΔV to the mission, which will multiply the mission’s mass and cost still more. The situation rapidly gets out of control and leads to the conclusion
that the opposition mission is virtually impossible unless nuclear thermal rocket (NTR) propulsion, which can have twice the exhaust velocity of a chemical rocket, or something even better is available. (For this reason the opposition mission has also been
favored
by some people advocating development of such systems.)

But why do we want to minimize mission time? The reasons classically given are that it is essential to minimize crew exposure to the twin menaces of zero-gravity and various types of space radiation. Because it spends nearly all of its time in interplanetary space, however, the opposition mission actually maximizes the zero-gravity exposure time of the crew. Furthermore, because radiation doses experienced per unit time in interplanetary space are estimated to be about a factor of four greater than those on the surface of Mars, where the atmosphere and surface material provide substantial shielding (even if no measures, such as throwing sand bags on the roof of the surface habitat, are taken), the radiation dose experienced by the crew on an sition mission is likely to be slightly greater than that on a conjunction mission.

Despite all the hand wringing over the danger of radiation on the way to Mars, it needs to be understood that neither of the doses shown in
Table 4.1
is especially threatening. To place them in perspective, we should note that every 60 rem of radiation received over an extended period, such as a several-year round-trip Mars mission, adds 1 percent of extra risk of a fatal cancer at some point later in life to a thirty-five-year-old woman, while 80 rem adds 1 percent of extra risk of fatal cancer to a thirty-five-year-old man. Radiation is not a major risk driver of a piloted Mars mission.

So, the advantages of the opposition mission are illusory, but its disadvantages are not. An opposition mission increases propulsion requirements, thereby increasing mission launch mass, and, consequently, mission cost. Hammering the hardware together for this enormous mass requires on-orbit assembly, which, when compared to integrating all hardware on Earth, boasts nearly zero quality control. Further, it maximizes the extent and complexity of such assembly, thereby maximizing the risk of misassembly. But it doesn’t stop there. The opposition mission requires more propellant than any other, and that transla
tes into longer engine burns over the course of the mission, which maximizes the risk of engine failure. The opposition mission also maximizes the transit flight time experienced on a single leg of the mission, which maximizes the reliability requirement for the ship’s life-support system (the conjunction ship’s life-support system must only be guaranteed for 180 consecutive days; the opposition must go for 430). The life-support system of the opposition-class mission also must handle exterior temperature excursions caused by traversing the solar system not just from Mars to Earth, but from Mars all the way in to Venus, where solar heating is twice that at Earth. (This is why some mission designers call the opposition mission’s Venus flyby maneuver a “Venus fryby.”) Finally, at the end of the mission, when the opposition-class spacecraft reaches the Earth, it hits the Earth’s atmosphere a lot harder than would be the case in a conjunction-class spacecraft. This maximizes the reentry deceleration forces on the spacecraft and the crew, and increases the risk that the spacecraft will, in the event of a misaligned reentry, either burn up or skip out of the atmosphere to leave the crew stranded in interplanetary space.

One enormous and absurd fault, though, looms over all of these flaws—the Opposition mission accomplishes next to nothing. After six months of traveling nearly 400 million kilometers to reach Mars, the spacecraft and crew spend just thirty days on Mars. With just a month in Mars orbit, the crew could hope, at best, to get two weeks on the surface before departure. In fact, if the weather is bad when the crew arrives, they might not get to land at all. The entire mission would have been a bust (recall
Mariner
9’s need to wait four months for a dust storm to clear after arrival). I liken the opposition mission plan to that of a family that decides to fly to Hawaii for Christmas vacation, spending ten days in transit flying from one airport to another, with half a day at the beach, weather permitting. Put simply, the opposition mission plan is just plain silly. It maximizes both cost and risk, and minimizes mission science return. It is favored only by those who wish to present a piloted Mars mission as a pipe dream, or who wish to increase the mission’s technical difficulty so as to justify funding some new propulsion system that they are pushing. Among those who are interested in actually getting humans to Mars, the opposition mission ha
s been dropped from all furth consideration.

Now between the various types of conjunction mission plans there is more room for rational choice. The minimum energy plan is the cheapest mission, but a fast-flight plan leads to a better mission, with a larger fraction of the total mission time spent on Mars doing useful exploration and less time wasted in transit. Flying to Mars on a fast conjunction profile drastically reduces the crew’s zero-gravity exposure time; cuts back on radiation exposure; and minimizes the in-space life-support system’s reliability requirements. However, because the minimum energy mission is not being pushed as fast, its ship can be made heavier, with more backups to various mission critical propulsion, control, and life-support systems. So, while a minimum energy spaceship needs to be more reliable than a fast conjunction craft, the mass budget is there to make it more reliable. (The opposition spacecraft, which must be made the
most
reliable, will have the
smallest
mass budget of all to support subsystem redundancy and reliability.)

There’s clearly a tradeoff here, and it’s necessary to make an intelligent compromise between spacecraft speed and system redundancy. But there’s another consideration. For certain departure velocities it is possible to go to Mars on a trajectory that will take you straight back to Earth if you decide not to (or for some reason can’t) go ahead with orbit capture at Mars. These are known as
free-return
trajectories. If the ship’s propulsion system fails completely during the outbound transit, or if the mission needs to be aborted for any other reason, following such trajectories can allow the crew to get home safely, just as was done in the nearly disastrous Apollo 13 mission, which employed a free-return trajectory to get to the Moon. The safety advantage of setting off to Mars on such trajectories is so obvious that considering outbound nonfree-return trajectories that might save thirty days, at best, is hardly worthwhile. In
Table 4.2
we list the options for free-return trajectories to Mars. The near minimum energy 3.34 km/s departure (option A) takes 250 days to get to Mars, and three years to get back to Earth (involving two 1.5 year period orbits), making it fine for cargo but a mediocre choice for a piloted flight. The 5.08 km/s departure (option B) cuts the transit to Mars down to 180 days and the free-return flight time to two years. This is clearly the best choice for piloted flight, beca
use flying to Mars on the higher-energy free-return trajectories (options C and D) not only requires expending a lot more propellant in exchange for a modest reduction in outbound transit time, but because their orbits will loop well out beyond Mars actually would cause the crew to take
longer
to get home if carrying out the free return should become necessary. In addition, the high-energy options will arrive at Mars traveling too fast for safe aerobraking.

Free-return capability is not a factor in choosing trajectories that go from Mars to Earth. However, transit-time reduction reaches a condition of diminishing returns when departure velocity starts to exceed 4 km/s. Trying to go much faster than this will simply force us to give up ship payload, and thus critical system redundancy, without reducing transit time appreciably.

Thus, we find that the
best
trajectories between Earth and Mars for a piloted Mars mission are those that leave Earth with a departure velocity of 5.08 km/s
(and no more)
and leave Mars with a departure velocity of about 4 km/s. For unpiloted cargo, either the Hohmann transfer or option A’s close-to-minimum-energy 3.34 km/s departure free-return trajectory is clearly best. So what’s the punch line? Simply this: these timal trajectories can easily be accomplished using state-of-the-art chemical propulsion.

—————

Note: The ΔV needed by a mission and its departure velocity are related but are not the same. For those who are interested, the mathematical relationships relating them to each other and to rocket specific impulse and mission mass are explained in a technical note at the end of this chapter.

TABLE 4.2
Free Return Trajectories between Earth and Mars

WHO GETS TO GO

So, now that
we’ve determined our trajectory, we need to select our crew—who, and how many.

“The more the merrier” summarizes much of the human-factors literature concerning crew size for a long duration Mars mission. However, since the number of crew members drives the mass of all habitats, transportation stages, and launch vehicles, it is essential to keep crew size to a minimum for reasons of cost and technical feasibility. Furthermore, no matter how many backup plans and abort options the mission design includes, we must understand that in sending a crew to Mars, we are, one way or another, sending a group of humans into harm’s way. Thus, from a moral point of view, the fewer people we have on board the initial missions, the better. Finally, no matter how desirable a large social group may appear to be for company on a long trip, any examination of the history of human exploration on Earth will show that it is entirely possible for long-duration expeditions to be carried out successfully by
one person
, two people, or any other number.