Simply Complexity (13 page)
Authors: Neil Johnson

In addition to its relevance to Complexity Science, it turns out that there is also an important consequence of this setup for standard economic theory. Specifically, there is no correct expectational model for this setup – if everybody made the same decision, it would automatically be the wrong decision since everyone would either stay away (in which case you should have turned up) or they all show up (in which case you should have stayed away). Hence the so-called “rational expectations” or “rational agent” model of standard economics breaks down. And since standard economic theory relies on the world being flooded with such typical people, our little example of bar-going turns out to be a huge wake-up call for Economics as a whole. Physicists don’t get off much lighter either – any attempt at a so-called mean-field theory based on a similar notion of a typical bar-goer, will not work for similar reasons.
Let’s develop this Friday night bar problem in a more scientific way. As we mentioned, this is an extremely important problem for Complexity Science, and as such is currently being studied by a large number of research groups from physics to finance, economics to sociology, computing to artificial intelligence, and geography to zoology. Irrespective of the specific application areas, all these researchers are interested in the same thing: the overall behavior of collections of decision-making objects, where the fact that there are only limited resources means that not everyone can win. Clearly an important ingredient is to sort out exactly what it means to win. In other words, how much reward, and similarly punishment, is there? Or put more simply, what is the “pain-gain” trade-off for each potential bar attendee?
It turns out that there are several ways of winning and losing in our bar problem. These are shown in
figure 4.1
. In particular, there are the following four potential outcomes each Friday night for every one of the
N
= 100 potential attendees:
First way of winning
: You decide to go to the bar, and the bar turns out to be under-crowded because less than sixty other
people turn up. For example, suppose the total number of people attending on that given Friday is only fifty. Since fifty is less than sixty, this means that it was the right choice to have attended – you have won! We can represent this mathematically by saying that the total number of people attending on a given Friday
t
is given by
n[t]
, where in this example we have
n[t]
= 50 with a comfort limit
L
= 60. You therefore win in situations where
n[t]
is less than, or equal to,
L
.
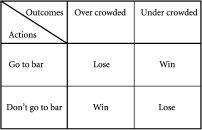
Figure 4.1
Knowing how to win, and knowing how to lose
First way of losing
: You decide to go to the bar, and the bar turns out to be over-crowded because more than sixty people turn up. In short, if you decide to attend in a given week
t
, you will lose if
n[t]
is greater than
L
.
Second way of winning
: You would also consider yourself a winner, if you decided
not
to attend and it turned out that the bar was over-crowded. In short, if you decide not to attend in a given week
t
, you will win if
n[t]
is greater than
L
.
Second way of losing
: You lose if you decide not to attend and it turned out that the bar was under-crowded. In short, if you decide not to attend in a given week
t
, you will lose if
n[t]
is less than, or equal to,
L
.
Associated with each of these outcomes, we can imagine that there is some kind of payoff – not necessarily monetary, but in terms of satisfaction. Now of course, we all might assign different levels of satisfaction or dissatisfaction to this process. But since we can assume that all potential attendees are pretty much alike in terms of what they want, we can take winning as corresponding to
gaining some kind of “unit of satisfaction” or “wealth”, and losing as paying out a similar unit of satisfaction or wealth. In other words, it is just like those family games that we play at Christmas or on vacations – indeed, this whole process of deciding whether or not to attend the bar is just one big game.
We now know what it means to win or lose in this game. But how should you go about deciding what to do? Let’s start by thinking what would happen if you had no memory of what you had decided to do in previous weeks, nor do you have any information about whether the bar was overcrowded or not. In short, you have no feedback from the past. We are also assuming that you have no idea about the number of other people
N
who are interested in attending. Hence you’d probably be tempted to flip a coin to decide what to do this coming Friday. In fact that is the best thing you can do, in the absence of any other knowledge. Therefore you would be deciding based on the toss of a coin – in other words, randomly. Indeed, things wouldn’t really change even if you knew some of the other possible attendees and were able to phone them to find out what they planned to do. It may turn out that they later change their minds. Furthermore, this is of course a competition for limited seating: so even if they told you what they planned on doing, should you automatically believe them?
Central to Complex Systems and hence Complexity is the presence of feedback. But so far, there isn’t any – and this is completely unrealistic since we all carry round some kind of memory of previous events. Regardless of whether this memory is correct, partially correct, or totally misguided, it does exist and will tend to bias our decisions in a given situation. So as regular bar-goers, we will probably remember what we did on a few previous Fridays and we will probably also know what, in hindsight, would have been the best thing to have done on those nights. We will therefore each be keeping, either consciously or unconsciously, some kind of running tally of how many past successes we have had. Hence we will have some kind of notion of whether our
methods of working out what to do – in other words, our strategies – need revising or not. The same thing would occur in a traffic setting, and in particular whether we choose a particular road home or not. We will remember whether we did or didn’t “win” in a few previous commutes home, based on our own memories of what we did and based on what we subsequently heard from other people or from the TV regarding the traffic on those nights.
But how specifically should we add this feedback? There are many, many ways of doing this – but it turns out that there are two principal setups that have been followed in the research community and which are featured in the publications listed in the Appendix. It is best to think of these two setups as sort of “vanilla” versions, to which different bells and whistles can be added. In particular, the two setups exhibit differing amounts of systematic and careless behavior by the bar-goers – in other words, differing amounts of systematic versus random decision-making as with the intern in
chapters 2
and
3
. The first setup involves bar-goers who are not very systematic, but neither are they too careless. This case is discussed in depth in this section, since it corresponds to the middle-ground behavior which so many of us actually follow. The second setup involves bar-goers who are almost completely systematic and leads to a far greater frustration among the population (the notion of frustration was discussed in
chapter 2
). Despite the differences in the two setups, and regardless of the bells and whistles which one then adds, it turns out that the same general phenomena – in particular, crowds and anticrowds – emerge in both setups.
We’ll focus here on the first setup involving bar-goers who are not very systematic in their decision-making, but neither are they too careless. In other words, they are not so systematic and reliable that they act like little computers – nor are they so random that they just use a simple coin-toss to decide their actions. Just as with the intern in
chapter 3
, we can mimic this middle-ground behavior with a coin whose outcome is biased by some feedback or memory from the past. However unlike our simple example in
chapter 3
, we will allow the specific way in which the coin-toss gets biased to differ for different people – and it will be through this individual bias that we will be able to mimic the real-world
situation whereby a given population of people typically contains a diversity of character types.
Let’s suppose that we are each carrying around a memory of our net number of past successes. In other words, we remember the tally given by the number of times we have won minus the number of times we have lost. If the number of losses exceeds the number of wins by too much, we will change the way in which we make our decisions – in other words, we will change our strategy. Just to be specific, let’s imagine that “too much” is a number
d
. But what is our strategy? We will suppose that all the potential attendees know what happened on the previous
m
Friday nights – for example, this could be
m
= 2 corresponding to the last two Friday nights. More specifically, they know whether the correct action on the previous
m
Fridays had been to go to the bar or not. In mathematical terms, they therefore know whether
n[t]
was less than or equal to
L
, or whether
n[t]
was greater than
L
. Let’s call these two outcomes 1 or 0, corresponding to whether the correct decision was to go to the bar or not. So an outcome 1 means that the correct decision was to have gone to the bar, while an outcome 0 means that the correct decision was to have not gone to the bar. In other words, we all effectively store 0’s or 1’s as a record of the past. For example, in the case where we remember the last two weeks’ outcomes, our record of the past outcomes might be 11 which means that the correct decision was to have gone to the bar on each Friday night. The other possibilities are 00 which means that the correct decision was to have not gone to the bar on each Friday night; 10 which means that the correct decision was to have gone to the bar two weeks ago, but not last week; 01 which means that the correct decision was to have not gone to the bar two weeks ago, but to have gone last week.
Suppose that on a given Friday, the previous
m
= 2 correct decisions were 11. We will imagine that each of the potential attendees remembers what happened the last time that this particular pattern 11 occurred. It may have been only a month or so ago, or much longer – it doesn’t matter. The same holds if the previous
m
= 2 correct decisions were 00, 10 or 01. In short, all potential attendees carry around a sort of crib-sheet containing a list of the winning decisions following the last time each pattern arose. This crib-sheet is therefore a source of common information.
So far, so good. Each bar-goer has a tally of past successes giving them a notion of how well their strategy is working – this represents their own piece of private information. They also have a crib-sheet telling them the correct decision following the last occurrence of each of the possible patterns that they will be faced with – this represents their public information. In fact, the public information could be broadcast by a public information system such as the radio or TV. All that matters is that all bar-goers know it, and it is the same for all of them.
Here is where their individual characters will now enter, by means of the biased coin which we mentioned earlier. Some of us might tend to think that given what happened the last time that a particular pattern of outcomes appeared, the same thing is likely to happen again – in other words, we believe that history repeats itself. On the other hand, others might think that it is precisely because it happened last time that the opposite will now happen. In other words they think that since the game is competitive, past history won’t repeat itself and instead the opposite will happen. Many of us might also lie between these two extremes – but quite where we sit will vary for each of us, and we may as individuals decide to change where we sit as time goes by. We can mimic these various possibilities by assuming that each potential bargoer has a coin which he tosses, where an outcome of heads means that he assumes that history will repeat itself. In other words, when faced with a given history such as 11, he simply looks at the crib-sheet to see what the correct decision turned out to be the last time that 11 occurred – and then he assumes that history will repeat itself if the outcome of his coin-toss is heads. By contrast, an outcome of tails means that he assumes that history will not repeat itself and instead the opposite will happen. In other words, when faced with a given history such as 11, he simply looks at the crib-sheet to see what the correct decision turned out to be the last time that 11 occurred – and then he makes the opposite decision.
To account for the different characters of the bar-goers, we can assume that the chances of throwing a heads or tails can differ for different people. In particular, we will say that the chance of throwing a heads, and hence assuming that history repeats itself,
is given by a number
p
for a particular person. This number could be 60 percent for example, in which case that person believes that history repeats itself 60 percent of the time, or equivalently six out of every ten times. In coin-toss jargon, we would say that this is represented by a probability of
p
= 0.6 of throwing a heads. Likewise the chance of throwing a tails, and hence assuming that history does not repeat itself, is 40 percent. This corresponds to a probability of (1-
p
) = 0.4 of throwing a tails. So the
p
value that somebody has, acts like a kind of character description. Somebody with a value of
p
= 1 will assume that history always repeats itself. Somebody with a value of
p
= 0 will assume that history
never
repeats itself and that the opposite will always happen. Somebody with a value of
p
= 0.5 is literally sitting on the fence – they are so uncertain about whether history will repeat itself or not, that they are continually switching between the two opposing points of view.