Power Hungry (8 page)
Authors: Robert Bryce

Wrestling the two terms to the ground requires real effort, particularly given that fact that many people make the mistake of using “power” and “energy” interchangeably. But we must persevere. Definitions matter. In order to properly address a problem, we must first define it and agree on a common set of terms. And given that our effort requires basic physics, the first stop on our power quest is the work done by a Scotsman whose last name has become synonymous with power: James Watt.
We use Watt's name on a near-daily basis. But few people know what a “watt” is or why Watt's work was so important. Here are the essential
facts: Watt, born in 1736, made critical improvements to the steam engine. Those inventions raised the efficiency of steam engines so much that Watt, having patented the improvements, became a wealthy man.
1
But Watt knew that improvements to the steam engine were not enough. He needed a metric that could help his customers understand the amount of work done by his steam engines in an hour or in a day. Given the centrality of horse-pulled power to eighteenth-century industry, and his ability to measure the work done by horses, it's not surprising that he dubbed his new unit a “horsepower.” The result of his various measurements: 1 horsepower = 33,000 foot-pounds per minute.
2
facts: Watt, born in 1736, made critical improvements to the steam engine. Those inventions raised the efficiency of steam engines so much that Watt, having patented the improvements, became a wealthy man.
1
But Watt knew that improvements to the steam engine were not enough. He needed a metric that could help his customers understand the amount of work done by his steam engines in an hour or in a day. Given the centrality of horse-pulled power to eighteenth-century industry, and his ability to measure the work done by horses, it's not surprising that he dubbed his new unit a “horsepower.” The result of his various measurements: 1 horsepower = 33,000 foot-pounds per minute.
2
The idea of foot-pounds per minute is hardly an intuitive metric, but in Watt's day it made sense. Watt did a lot of work with coal mines, where horses were the draft animal of choice. Of course, a horse couldn't lift a bucket of coal weighing 33,000 pounds. But that same horse could likely raise 330 pounds of coal 100 feet in 1 minute. Or it might be able to lift 33 pounds of coal 1,000 feet in that same time frame. The combination of feet and pounds can be whatever numbers you choose. But if the product of the two numbers equals 33,000 foot-pounds per minute, then you are producing 1 horsepower.
3
3
Since Watt's day, horsepower has coexisted with other measures of power, including Btu per hour, calories per day, kilocalories per minute, and ergs per second, to name just a few. For decades, this welter of power metrics confused even the most savvy of scientists and laymen. In 1960, the International System of Units, commonly called SI, was established. SI units are the result of a centuries-long effort to create a uniform system of measurement for distance, mass, time, current, power, pressure, and temperatureâyou name itâas well as symbols for numbers in the thousands, millions, billions, and so on. SI facilitates analysis and discussion, particularly among people from different cultures, languages, and fields of interest. And, know it or not, SI parlance has become part of our everyday speech. Kilo (k) means thousand, as in kilogram or kilowatt. Similarly, mega (M) means million, as in megajoule or megawatt, and giga (G) means billion, as in gigabyte or gigaflop. (See Appendix B for a full listing of SI numerical designations.)
SI simplified discussions of energy and power. The joule (J), named after the British scientist James Prescott Joule, is the only unit of measure
in SI for any kind of energy, regardless of its form.
4
The watt (W)ânamed for James Watt some six decades after his deathâis the only unit of measure in SI for any kind of power.
in SI for any kind of energy, regardless of its form.
4
The watt (W)ânamed for James Watt some six decades after his deathâis the only unit of measure in SI for any kind of power.
To differentiate between joules and watts, it may help to think of them thusly: The total amount of energy produced is measured in joules; power generation is measured in watts. Put another way, the quantity of energy consumed is measured in joules; how quickly that energy gets consumed is measured in watts.
5
Thus, operating a 60-watt light bulb requires power, which, as just discussed, is measured in watts. After an hour, when you switch the light off, you can then measure the amount of energy that was consumed by the light, which is measured in joulesâor in kilowatt-hours or in Btuâall of which are measures of energy.
5
Thus, operating a 60-watt light bulb requires power, which, as just discussed, is measured in watts. After an hour, when you switch the light off, you can then measure the amount of energy that was consumed by the light, which is measured in joulesâor in kilowatt-hours or in Btuâall of which are measures of energy.
Watts and joules are often used together. Calculating power requires knowing the amount of energy and the time over which it was used. This calculation has become a basic formula in physics. The equation is simple:
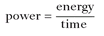
One watt is equal to 1 joule per second. The corollary is just as important: 1 joule = 1 watt-second.
6
With the notable exception of the United States, the entire world uses SI when discussing energy and power. Though SI units are valuable and laudable, it doesn't mean that everyone who uses them comprehends them. Indeed, although the watt has become a standard unit for measuring power, horsepower continues to be part of our everyday discussions, particularly when we are talking about cars, chainsaws, and lawnmowers. Why? It's a centuriesold metric that's easy for most laymen to grasp. Everyone can imagine a horse pulling a plow or a carriage and the work that that job entails. So which metric makes more sense? During the course of writing this book, I asked dozens of people which term they understood betterâwatts or horsepower. Some people replied with a blank stare and chose neither. A handful (including nearly all of the engineers and scientists) preferred watts. But the majority preferred horsepower. Asked why, they said that they were more familiar with horsepower ratings on cars than they were with power ratings listed in watts. Men generally preferred horsepower. Women generally picked watts. Thus, my sample
may have been skewed because the population I surveyed had more males than females.
6
With the notable exception of the United States, the entire world uses SI when discussing energy and power. Though SI units are valuable and laudable, it doesn't mean that everyone who uses them comprehends them. Indeed, although the watt has become a standard unit for measuring power, horsepower continues to be part of our everyday discussions, particularly when we are talking about cars, chainsaws, and lawnmowers. Why? It's a centuriesold metric that's easy for most laymen to grasp. Everyone can imagine a horse pulling a plow or a carriage and the work that that job entails. So which metric makes more sense? During the course of writing this book, I asked dozens of people which term they understood betterâwatts or horsepower. Some people replied with a blank stare and chose neither. A handful (including nearly all of the engineers and scientists) preferred watts. But the majority preferred horsepower. Asked why, they said that they were more familiar with horsepower ratings on cars than they were with power ratings listed in watts. Men generally preferred horsepower. Women generally picked watts. Thus, my sample
may have been skewed because the population I surveyed had more males than females.
This book will use both horsepower and watts. Pick whichever unit you preferâjust remember that both are measures of power, not energy, and keep in mind that 1 horsepower is equal to 746 watts.
Now that the mini-lecture on physics and SI is done, we must return to the task at hand: defining
energy
and
power
. One of the best explanations I've heard comes from my good friend Stan Jakuba, a whipsmart engineer who has spent decades advocating the virtues and simplicity of SI. “Energy has many forms,” he explains, “such as electricity, heat, work, kinetic energy, potential energy, chemical energy, nuclear energy, etc. Energy can be visualized as an amount of something. Power is the energy
flow
.”
energy
and
power
. One of the best explanations I've heard comes from my good friend Stan Jakuba, a whipsmart engineer who has spent decades advocating the virtues and simplicity of SI. “Energy has many forms,” he explains, “such as electricity, heat, work, kinetic energy, potential energy, chemical energy, nuclear energy, etc. Energy can be visualized as an amount of something. Power is the energy
flow
.”
Jakuba's vivid explanation underscores an essential concept: Energy is an amount, while power is a measure of energy flow. And that's a critical distinction. Energy is a sum. Power is a rate. And rates are often more telling than sums.
To illustrate that fact, let's express energy and power in oil terms. Energy is measured in barrels. Power is measured in barrels
per day
. Suppose you have discovered an oil field containing 1 billion barrels of oil. That's a lot of energy, sure. But that energy is worthless unless it can be brought out of the ground. And, generally speaking, the faster you can get it out, the better. Thus, an oil field that holds, say, 100 million barrels of oil that can produce 10,000 barrels per day is worth a whole lot moreâwe can even say it is more
powerful
âthan one that produces 10,000 barrels per week.
per day
. Suppose you have discovered an oil field containing 1 billion barrels of oil. That's a lot of energy, sure. But that energy is worthless unless it can be brought out of the ground. And, generally speaking, the faster you can get it out, the better. Thus, an oil field that holds, say, 100 million barrels of oil that can produce 10,000 barrels per day is worth a whole lot moreâwe can even say it is more
powerful
âthan one that produces 10,000 barrels per week.
The key word here is “per.” When buying a car, we want to know the rates: How many miles
per
gallon does it get, how fastâin miles
per
hourâcan it go?
per
gallon does it get, how fastâin miles
per
hourâcan it go?
Yet another good analysis comes from Richard Muller's 2008 book
Physics for Future Presidents
, in which he writes, “For power and energy, the kilowatt is the rate of energy delivery (the power) and the kilowatt-hour is the total amount of energy delivered.”
7
Combining Muller's explanation with Jakuba's provides yet one more way to conceive of energy and power: The kilowatt-hour gives us a tally of the energy provided, whereas the kilowatt measures the rate of energy flow. And that rate of
energy flow can be measured in watts, kilowatts, megawatts, gigawatts, terawatts, or, of course, in horsepower, thousands of horsepower, millions of horsepower, and so on.
Physics for Future Presidents
, in which he writes, “For power and energy, the kilowatt is the rate of energy delivery (the power) and the kilowatt-hour is the total amount of energy delivered.”
7
Combining Muller's explanation with Jakuba's provides yet one more way to conceive of energy and power: The kilowatt-hour gives us a tally of the energy provided, whereas the kilowatt measures the rate of energy flow. And that rate of
energy flow can be measured in watts, kilowatts, megawatts, gigawatts, terawatts, or, of course, in horsepower, thousands of horsepower, millions of horsepower, and so on.
Energy doesn't produce wealth. Energy
use
produces wealth, and the majority of the energy we use is fed into engines, turbines, and motors to produce power. It's converting energyâof whatever typeâinto motion that gives it value. And that's what engines do: They convert energy into mechanical motion that can be used for doing work. As Jakuba cleverly phrased it, the more we increase
the energy flow
through those engines, the more power we get. And the more power we have, the more work we can do.
use
produces wealth, and the majority of the energy we use is fed into engines, turbines, and motors to produce power. It's converting energyâof whatever typeâinto motion that gives it value. And that's what engines do: They convert energy into mechanical motion that can be used for doing work. As Jakuba cleverly phrased it, the more we increase
the energy flow
through those engines, the more power we get. And the more power we have, the more work we can do.
That leads to another key point: The very word “power” implies control. When it comes to doing work, we insist on having power that is instantly available. We want the ability to switch things on and off whenever we choose. And that desire largely excludes wind and solar from being major players in our energy mix, because we can't control the wind or the sun. Weather changes quickly. A passing thunderstorm or high-pressure system can take wind- and solar-power systems from full output to zero output in a matter of minutes. The result: We cannot reliably get or deliver the power from those sources at the times when it is needed.
Renewable energy
has little value unless it becomes
renewable power
, meaning power that can be dispatched at specific times of our choosing. But achieving the ability to dispatch that power at specific times means solving the problem of energy storage. And despite decades of effort, we still have not found an economical way to store large quantities of the energy we get from the wind and the sun so that we can convert that energy into power when we want it.
has little value unless it becomes
renewable power
, meaning power that can be dispatched at specific times of our choosing. But achieving the ability to dispatch that power at specific times means solving the problem of energy storage. And despite decades of effort, we still have not found an economical way to store large quantities of the energy we get from the wind and the sun so that we can convert that energy into power when we want it.
Which renewable sources can provide clean renewable power? One of the best is geothermalâwhich can provide a constant flow of predictable power that can be dispatched when needed. By October 2009, the United States had about 3,100 megawatts of geothermal production capacity. And geothermal promoters were predicting that they could triple that quantity to about 10,000 megawatts of baseload power capacity.
8
That could help, but it would still be a trifle when compared to the total U.S. generating capacity of 1 million megawatts.
8
That could help, but it would still be a trifle when compared to the total U.S. generating capacity of 1 million megawatts.
The hype over renewables can only be debunked by thoughtfully walking through the numbers and the terms. And the most important of the terms are the first two items of the Four Imperatives: power density and energy density.
Power density
refers to the amount of power that can be harnessed in a given unit of volume, area, or mass.
9
Examples of power-density metrics include horsepower per cubic inch, watts per square meter, and watts per kilogram. (In Part 2, I will show why watts per square meter may be the most telling of these. Using watts per square meter allows us to make a direct comparison between renewable energy sources such as wind and solar and traditional sources such as oil, natural gas, and nuclear power.)
refers to the amount of power that can be harnessed in a given unit of volume, area, or mass.
9
Examples of power-density metrics include horsepower per cubic inch, watts per square meter, and watts per kilogram. (In Part 2, I will show why watts per square meter may be the most telling of these. Using watts per square meter allows us to make a direct comparison between renewable energy sources such as wind and solar and traditional sources such as oil, natural gas, and nuclear power.)
Energy density
refers to the amount of energy that can be contained in a given unit of volume, area, or mass. Common energy density metrics include Btu per gallon and joules per kilogram.
10
refers to the amount of energy that can be contained in a given unit of volume, area, or mass. Common energy density metrics include Btu per gallon and joules per kilogram.
10
When it comes to questions about power and energy, the higher the density, the better. For example, a 100-pound battery that can store, say, 10 kilowatt-hours of electricity is better than a battery that weighs just as much but can only hold 5 kilowatt-hours. Put another way, the first battery has twice the energy density of the second one. But both of those batteries are mere pretenders when compared with gasoline, which, by weight, has about eighty times the energy density of the best lithium-ion batteries.
As our society develops and urbanizes, we are seeking to use power in ever-greater quantities in ever-smaller places, and that is particularly true in our cities. Watt's breakthroughs increased the efficiency of the steam engine. Put another way, he increased the power density of the engine by designing it to produce more power from the same amount of space and from the same amount of coal. Ever since Watt's day, the world of engineering has been dominated by the effort to produce ever-better engines that can more quickly and efficiently convert the energy found in coal, oil, and natural gas into power. And that effort to increase the power density of our engines, turbines, and motors has resulted in the production of ever-greater amounts of power from smaller and smaller spaces.
The evolution of power density can be visualized by comparing the engine in the Model T with that of a modern vehicle. In 1908, Henry
Ford introduced the Model T, which had a 2.9-liter engine that produced 22 horsepower, or about 7.6 horsepower per liter of displacement.
11
A century later, Ford Motor Company was selling the 2010 Ford Fusion. It was equipped with a 2.5-liter engine that produced 175 horsepower, which works out to 70 horsepower per liter.
12
Thus, even though the displacement of the Fusion's engine is about 14 percent less than the one in the Model T, it produces more than nine times as much power per liter.
13
In other words, over the past century, Ford's engineers have made a nine-fold improvement in the engine's power density.
Ford introduced the Model T, which had a 2.9-liter engine that produced 22 horsepower, or about 7.6 horsepower per liter of displacement.
11
A century later, Ford Motor Company was selling the 2010 Ford Fusion. It was equipped with a 2.5-liter engine that produced 175 horsepower, which works out to 70 horsepower per liter.
12
Thus, even though the displacement of the Fusion's engine is about 14 percent less than the one in the Model T, it produces more than nine times as much power per liter.
13
In other words, over the past century, Ford's engineers have made a nine-fold improvement in the engine's power density.
Other books
The Devil's Gold by Steve Berry
Pickle Pizza by Beverly Lewis
Driven to Ink by Olson, Karen E.
Hot Wheels by William Arden
I Know What You Did Last Summer by Lois Duncan
Blame It on Texas by Christie Craig
Exit Stage Left by Graham Ison
The Gap into Madness: Chaos and Order by Stephen R. Donaldson
Girl With Guitar by Caisey Quinn
The Rushers by J. T. Edson